Показатели в математике (целые, дробные + функция) с примерами и образцами

Оглавление:

Показатель — это число, показывающее, в какую именно степень возводится основание.

Показатель — в большинстве случаев, обобщённая характеристика какого-либо объекта, процесса или его результата, понятия или их свойств, обычно, выраженная в числовой форме.

Целые показатели

Свойства целых положительных показателей: Показатели степени до сего времени предполагались нами целыми и положительными, причём мы им придавали смысл, выражаемый в следующем определении:

Возвысить число а в степень с целым и положительным показателем n — значит найти произведение n одинаковых сомножителей aaa…a.

Перечислим свойства этих показателей, известные нам из предыдущих глав алгебры:

1) при умножении степеней одного и того же числа показатели их складываются;
2) при делении степеней одного и того же числа показатель делителя вычитается из показателя делимого, если показатель делителя не больше показателя делимого;
3) при возвышении отрицательного числа в степень с чётным показателем получается положительное число, а с нечётным показателем — отрицательное;
4) чтобы возвысить в степень произведение, достаточно возвысить в эту степень каждый сомножитель отдельно;
5) чтобы возвысить степень в степень, достаточно перемножить показатели этих степеней;
6) чтобы возвысить в степень дробь, достаточно возвысить в эту степень отдельно числитель и знаменатель;
7) чтобы возвысить радикал в степень, достаточно возвысить в эту степень подкоренное выражение;
8) чтобы извлечь корень из степени, достаточно разделить показатель степени на показатель корня, если такое деление выполняется нацело.

Теперь мы расширим понятие о показателях, введя показатели отрицательные и дробные, которых до сего времени мы не употребляли. Мы увидим при этом, что все свойства целых положительных показателей сохраняются и для показателей отрицательных и дробных.

Нулевой показатель

При делении степеней одного и того же числа показатель делимого может оказаться равным показателю делителя.

Пусть нужно разделить аⁿ на аⁿ.

Применяя правило (2), получаем:
aⁿ : aⁿ =aⁿ⁻ⁿ = α⁰.

Но нуль, как показатель степени, не имеет того значения, которое придаётся показателям целым и положительным, так как нельзя повторить число сомножителем нуль раз. Чтобы придать смысл выражению α⁰, подойдём к вопросу о делении аⁿ на аⁿ с другой стороны. Мы знаем, что при делении любого (отличного от нуля) числа на равное ему число частное равно единице.

Поэтому условились считать α⁰=l.

Таким образом, по определению:
Всякое число (за исключением нуля) в нулевой степени равно единице.

Легко убедиться в том, что перечисленные выше свойства целых положительных показателей применимы и к нулевому показателю. Так: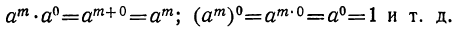
Показатели

Отрицательные целые показатели

Условимся при делении степеней одного и того же числа вычитать показатель делителя из показателя делимого и в том случае, если показатель делителя больше показателя делимого. Тогда мы получим в частном букву с отрицательным показателем, например: α² : α⁵= α⁻³. Таким образом, число с отрицательным показателем мы условимся употреблять для обозначения частного от деления степеней этого числа в том случае, когда показатель делителя превосходит показатель делимого на столько единиц, сколько их находится в абсолютной величине отрицательного показателя. Так, α⁻² означает частное α : α³, или α² : α⁵, или α³ : α⁵, вообще частное α ͫ : α ͫ ⁺².

Применяемое в этом смысле число с отрицательным показателем равно дроби, у которой числитель 1, а знаменатель — то же число, но с положительным показателем, равным абсолютной величине отрицательного показателя.

Действительно, согласно нашему условию, мы должны иметь: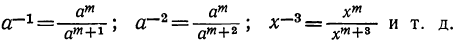
Показатели

Сократив две первые дроби на ат и третью дробь на хт (т. е. в обоих случаях сократив дроби на числитель), получим: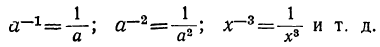
Показатели

Вообще: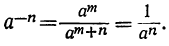
Показатели

Заметим, что отрицательные показатели дают возможность представить всякое дробное алгебраическое выражение под видом целого; для этого стоит только все множители знаменателя перенести множителями в числитель, взяв их с отрицательными показателями. Например: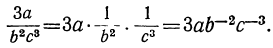
Показатели

Действия над степенями с отрицательными показателями

Убедимся теперь, что все действия над степенями с отрицательными показателями можно производить по тем же правилам, какие были прежде выведены для показателей положительных. Достаточно обнаружить это только для умножения и возвышения в степень, так как правила обратных действий — деления и извлечения корня — являются следствиями правил прямых действий.

Умножение

Предстоит показать, что при умножении степеней показатели одинаковых букв складываются и в том случае, когда эти показатели отрицательные. Убедимся, что 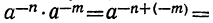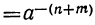, где m и n — целые положительные числа.

Действительно, заменив степени с отрицательными показателями дробями и произведя действие умножения по правилам, относящимся к дробям, получим: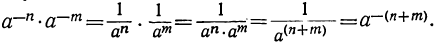
Показатели

Подобно этому: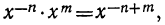
Показатели так как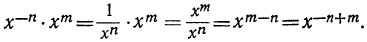

Возвышение в степень

Надо показать, что при возвышении в степень показатели этих степеней перемножаются и в том случае, когда они отрицательные. Убедимся, что .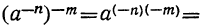

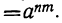Действительно: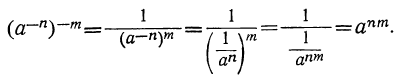
Показатели

Подобно этому: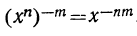
Показатели , потому что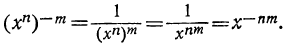

Примеры:
1) (3α⁻ ²b²c⁻ ³) (0,8ab⁻ ³ c⁴)=2,4α⁻ ¹b⁻ ¹ c.
2) (x⁻ ¹ y³ z²) : (5x²y⁻ ² z³ ) = 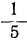Показатели x⁻ ³y⁵z⁻ ¹ .
3) (2αx⁻ ³ )⁻ ² =2⁻ ² α⁻ ² x⁶.
4) (х⁻ ² — у⁻ ¹ )² =(x⁻ ² ) ² — 2x⁻ ² y⁻ ¹ +(y⁻ ¹ ) ² =x⁻ ⁴ — 2x⁻ ² y⁻ ¹ +y⁻ ² .
5) (a⁻ ² + b⁻ ³ ) (а⁻ ² — b⁻ ³ )=a⁻ ⁴ — b⁻ ⁶.
6) 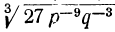Показатели =3p⁻ ³ q⁻ ¹.

Дробные показатели

В каком смысле употребляются дробные показатели: Мы знаем, что при извлечении корня из степени делят показатель степени на показатель корня, если такое деление выполняется нацело; например: 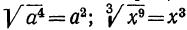и т. д. Условимся теперь распространять это правило и на те случаи, когда показатель степени не делится нацело на показатель корня. Например, мы условимся принимать, что: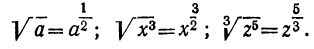
Показатели

Вообще мы условимся, что:
Выражение 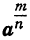означает корень, показатель которого равен знаменателю, а показатель степени подкоренного числа равен числителю показателя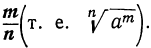 Показатели

Условимся употреблять отрицательные дробные показатели в том же смысле, в каком мы употребляли отрицательные целые показатели; например, условимся, что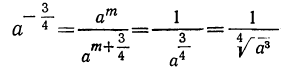

Основное свойство дробного показателя

Величина степени с дробным показателем не изменится, если мы умножим или разделим на одно и то же число (отличное от нуля) числитель и знаменатель дробного показателя.
Так: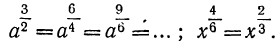
Показатели

Вообще: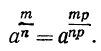
Показатели

Действительно, знаменатель дробного показателя означает показатель корня, а числитель его означает показатель степени подкоренного выражения, а такие показатели, как мы видели, можно умножать и делить на одно и то же число.

Основываясь на этом свойстве, мы можем преобразовывать дробный показатель совершенно так же, как и обыкновенную дробь; например, мы можем сокращать дробный показатель или приводить несколько дробных показателей к одному знаменателю.

Действия над степенями с дробными показателями

Предстоит доказать, что к дробным показателям применимы правила, выведенные раньше для целых показателей. Это достаточно обнаружить только для умножения и возвышения в степень, так как правила деления и извлечения корня являются следствиями правил умножения и возвышения в степень.

Умножение

Докажем, что при умножении показатели степеней одинаковых букв складываются и тогда, когда эти показатели дробные. Например, убедимся, что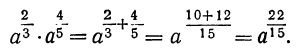

Для этого изобразим степени с дробными показателями в виде радикалов и произведём умножение по правилу умножения радикалов: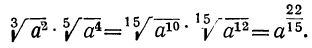
Показатели

Результат получился тот же самый, какой мы получили после сложения показателей; значит, правило о сложении показателей (при умножении) можно применять и для дробных показателей.
Таким образом: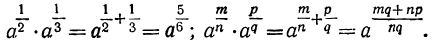
Показатели

Возвышение в степень

Докажем, что при возвышении степени в степень показатели степеней можно перемножать и тогда, когда эти показатели дробные. Например, убедимся, что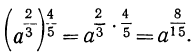

Действительно, заменив радикалами степени с дробными показателями и произведя действия над радикалами, получим: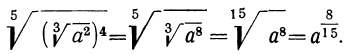
Показатели

Если показатели не только дробные числа, но и отрицательные, то и тогда к ним можно применять правила, доказанные раньше для положительных показателей. Например: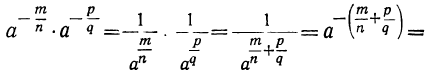

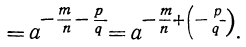
Примеры на действия с дробными и отрицательными показателями

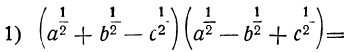
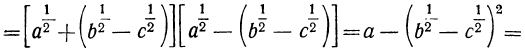
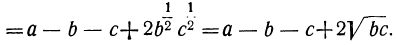
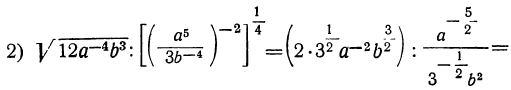
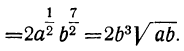
Показатели

Понятие об иррациональном показателе

Смысл степени с иррациональным показателем:

Рассмотрим степени 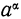Показатели , в которых α — какое-нибудь иррациональное число, когда основание степени α есть какое-нибудь положительное число, не равное 1. При этом могут представиться следующие три случая:

a) α > 1 и α — положительное иррациональное число; например, 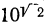Показатели .

Обозначим через α₁ любое рациональное приближённое значение числа α, взятое с недостатком, и через α₂ — любое приближённое рациональное значение числа а, взятое с избытком. Тогда степень 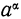Показатели , означает таксе число, которое больше всякой степени 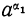, но меньше всякой степени 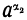. Можно доказать, что такое число существует, и единственно. Например, 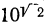означает такое число, которое больше каждого из чисел ряда:

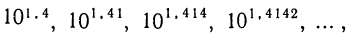
в котором показатели — десятичные приближённые значения 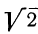, взятые с недостатком, но меньше каждого из чисел ряда: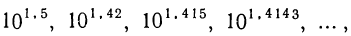

в котором показатели — десятичные приближения V 2, взятые с избытком.

б) a < 1 и α — по-прежнему положительное иррациональное число, например, 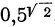Показатели .

Тогда под степенью 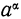Показатели разумеют такое число, которое меньше всякой степени 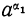, но больше всякой степени 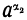. Так, 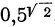есть число, меньшее каждого из чисел ряда: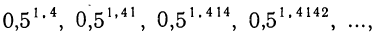

но большее каждого из чисел ряда: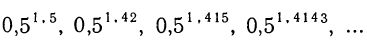
Показатели

Таким образом, если иррациональное число а заключено между двумя рациональными числами α₁ и α₂, то степень 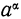Показатели заключена между степеням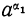и и 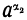и тогда, когда α > 1, и тогда, когда α < l.

в) Показатели и α — отрицательное иррациональное число; например: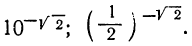

Тогда выражению 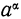Показатели придают тот же смысл, какой имеют степени с отрицательными рациональными показателями. Так: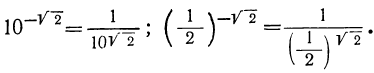

При подробном рассмотрении теории иррациональных показателей обнаруживается, что все свойства показателей рациональных применимы и к показателям иррациональным; так: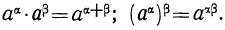
Показатели

Показательная функция

Определение:

Показательной функцией называется функция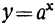 Показатели , представляющая собой степень, у которой основание а есть какое-нибудь постоянное положительное число, не равное 1, а показатель х — независимое переменное, могущее принимать всевозможные значения, положительные и отрицательные, целые и дробные, рациональные и иррациональные. При этом предполагается, что в том случае, когда показатель х равен дроби и, следовательно, когда 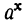Показатели означает радикал некоторой степени, то из всех значений радикала берётся только одно арифметическое, т. е. положительное.

Из того, что мы знаем о показателях степени, следует, что функция 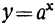Показатели при всяком значении х имеет единственное значение (благодаря условию брать для радикалов только арифметическое значение).

Свойства показательной функции

Рассмотрим некоторые свойства показательной функции, помня, что а мы считаем положительным числом.

1. При всяком положительном основании функция 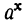Показатели положительна, т. е. 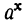> 0.
При х целом положительном 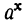>0, каково бы ни было положительное число а; следовательно, высказанное нами положение в этом случае справедливо.

Пусть теперь х равно некоторой положительной дроби, например
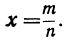Показатели Тогда: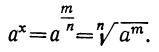

Но 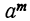Показатели > 0, следовательно, и 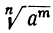> 0, так как мы условились брать лишь арифметическое значение корня.

Пусть х — положительное иррациональное число. Обозначим через α₁ и a₂ приближённые рациональные значения х по недостатку и избытку. Эти приближённые значения можно выбрать положительными. Тогда значение 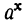Показатели , будучи заключённым между двумя положительными числам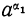и и 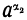, является положительным числом.

Пусть, наконец, х равно некоторому отрицательному числу, например x=—р. Тогда: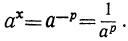
Показатели

Каково бы ни было положительное число р, согласно предыдущему 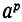Показатели > 0, но тогда и .

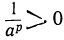Таким образом, высказанное нами положение справедливо для всякого х.

2. При a > 1 функция 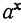Показатели >l, если х>0, и 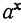< l, если x < 0 (при a < l знаки неравенства для 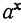противоположны).

Пусть х — целое положительнее число. Тогда: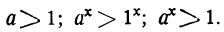
Показатели

Пусть х — положительная дробь, например 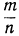Показатели . Тогда: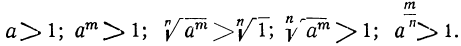

Если х — положительное иррациональное число, то 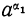Показатели > 1, где a₁ — приближённое рациональное значение х по недостатку, а поэтому и . Таким образом, при всяком положительном х

Пусть теперь х есть какое-либо отрицательное число, например x = —р. Тогда: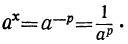
Показатели

Но согласно предыдущему 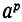Показатели > 1. Следовательно: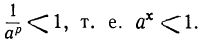

При a>1 функция 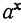Показатели возрастает при возрастании х.

Если x₁ и x₂ — два целых положительных числа и x₂ > x₁, то очевидно, что при 1 будем иметь: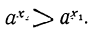
Показатели

Пусть теперь x₁ и x₂ — положительные дроби, например x₁= 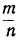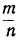Показатели и x₂ =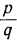. Пусть также 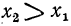. Тогда: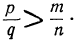

Или по приведении дробей к одному знаменателю: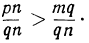
Показатели

Из двух неравных дробей с одинаковыми знаменателями та больше, у которой числитель больше. Следовательно:
Показатели

Так как рn и mq — целые числа, то к ним можно применить предыдущие рассуждения и мы получим: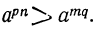
Показатели

Извлечём из 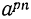Показатели и 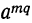корень степени qn. Мы знаем, что из двух корней одинаковой степени тот больше, у которого больше подкоренное число. Следовательно: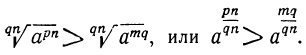

Сокращая показатели, получим: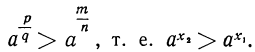

Пусть x₁ и x₂ — два вещественных числа, из которых одно или оба иррациональны.

Обозначим через β приближённое рациональное значение x₁ по избытку, а через а приближённое значение x₂ по недостатку. Если x₁ < x₂, то можно выбрать а и β при условии β < α. Тогда будем иметь 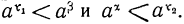Показатели Но так как , то .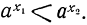

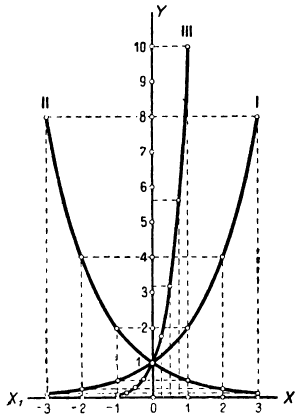
График показательной функции. Построим график следующих трёх показательных функций:
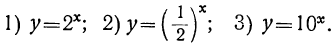
Показатели

Для построения графиков первых двух функций мы дадим переменному числу х ряд целых значений:
-3; -2; -1; 0; 1; 2; 3.

При x=—3 мы получим: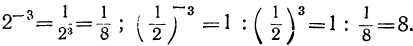
Показатели

Подобно этому вычислим значения у и для всех остальных значений x.

Для функции 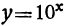Показатели неудобно брать указанные значения числа х, так как мы получили бы тогда для у такие большие числа, которые на чертеже 29 не умещаются (например, при х = 3 мы получили бы y= 10³ = 1000). Для этой функции мы возьмём такие дробные значения (заключающиеся между —1 и +1):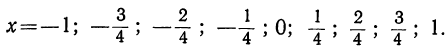
Показатели

Соответствующие значения у вычислим в такой последовательности: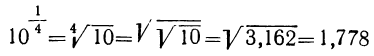
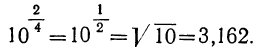
Показатели

Далее простым умножением и делением находим: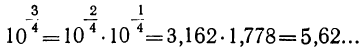
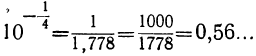
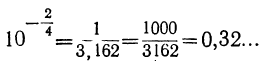
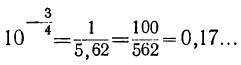
Показатели

Выпишем все найденные значения в следующие три таблицы: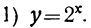
Показатели

x =	возрастает	-3	-2	-1	0	1	2	3	возрастает
y =	возрастает		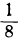		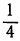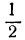1	2	4	8	возрастает

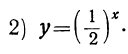
Показатели

x =	возрастает	-3	-2	-1	0	1	2	3	возрастает
y =	возрастает	8	4	2	1		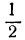		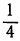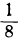возрастает

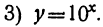
Показатели

x =	возрастает	-1		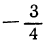		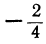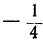0		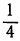		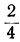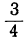1	возрастает
y =	возрастает	0,1	0,17	0,32	0,56	1	1,78	3,16	5,62	10	возрастает

(в последней таблице числа округлены).

Нанеся эти значения на чертёж и соединяя полученные точки кривыми, мы получим (черт. 29) три графика взятых функций (удобно чертёж выполнить на миллиметровой бумаге, беря за единицу длины сантиметр).

Рассматривая графики показательных функций, мы видим на них в наглядном изображении следующие свойства:

При всяком положительном основании функция 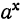положительна (все кривые расположены выше оси х-ов).
При α > 1 функция 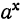> 1, если х > 0, и 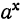< 1, если х < 0 (при а < 1 знаки неравенств для 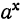противоположны).
При возрастании х функция ах возрастает, если а > 1 (и убывает, если a < l).
Если х=0, то 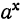=1 при всяком а (все кривые проходят через одну и ту же точку, лежащую на оси у-ов и отстоящую от точки 0 на +1).
При a > 1 функция при возрастании х возрастает тем быстрее, чем больше а (кривая при a = 10 поднимается вверх значительно больше, чем при a=2).

Решение заданий и задач по предметам:

Дополнительные лекции по высшей математике: