Дифференциальные теоремы о среднем с примерами решения и образцами выполнения

Оглавление:

Теоремы о среднем значении:

Теорема Ролля

Теорема:

Если функция f(x)

1) непрерывна на отрезке [а, b);

2) имеет производную хотя бы на интервале (а, b);

3) на концах отрезка [а, b] принимает равные значения (f(a) = f(b)),

то в интервале (а, b) существует п о крайней мере одна точка в которой производная данной функции равна нулю:

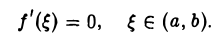
Так как по условию функция f(x) непрерывна на отрезке [а, b], то в силу второй теоремы Вейерштрасса она на этом отрезке принимает наименьшее и наибольшее значения. Обозначим их соответственно т и М. Могут представиться два случая:

1) М = т. В этом случае М ≤ f(х) ≤ М, т. е. f(x) есть постоянная на [а, b]. Поэтому f'(x) = 0 во всем интервале (а, b), так что в этом случае теорема верна.

2) М ≠ т. Тогда функция f(x) по крайней мере одно из двух своих значений М или m принимает в точке ξ содержащейся внутри интервала (а, b), так как f(а) = f(b) и потому не может быть одновременно М значением f(х) на одном конце. а т — на другом конце отрезка [а, b]. Пусть для определенности M = f( ξ ), а < ξ < v (рис. 1).

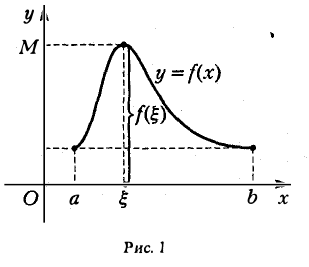
Так как по условию f(х) имеет производную f'(x) в каждой точке х интервала (а, b), то существует и f'( ξ ) и

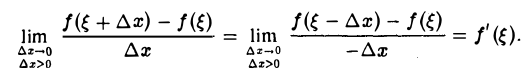
Но f( ξ ) = М — наибольшему значению функции f(х) на отрезке (а, b] и поэтому

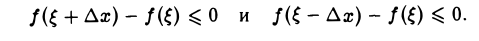
Отсюда

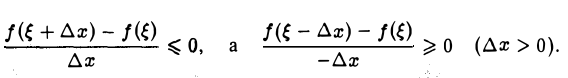
Переходя в этих неравенствах к пределу при ∆х —► 0, получим два неравенства

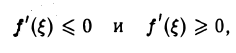
которые должны быть верны одновременно. Следовательно, f'( ξ ) = 0, т.е. теорема верна и для этого случая.

Теореме Ролля можно дать следующее геометрическое истолкование. Пусть имеем кривую ∼ АВ, заданную уравнением у = f(x), где функция f(x) на отрезке [а, b] удовлетворяет всем условиям теоремы Ролля. Это означает, что

1) кривая ∼ АВ непрерывна на [а, &];

2) в любой точке кривой, находящейся между точками А (а, f(а)) и В (b, f(b)), можно провести касательную к этой кривой;

3) концы дуги ∼ АВ кривой находятся на одном уровне по отношению к оси Ох (рис.2).

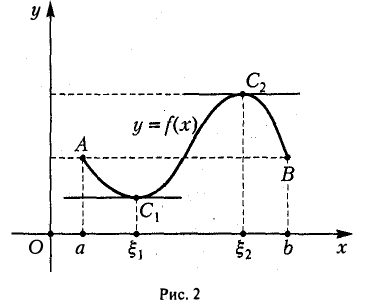
Утверждение теоремы Ролля состоит в том, что на дуге ∼ АВ кривой, обладающей указанными свойствами, найдется по крайней мере одна точка С(( ξ , f( ξ )), в которой касательная к данной кривой параллельна оси Ох (или хорде АВ).

Условия теоремы Ролля являются существенными и при их нарушении утверждение теоремы может оказаться несправедливым.

Пример:

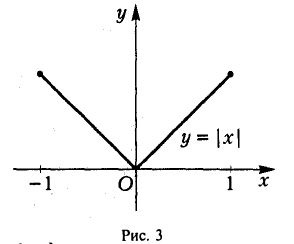
Так, например, для функции f(х) = |х|, -1 ≤ х ≤ 1, (рис.3) выполнены все условия теоремы Ролля, кроме существования производной f'(х) в интервале (-1,1). Не существует f'(х) в одной только точке х = 0, и утверждение теоремы Ролля к данной функции уже неприменимо, так как в интервале (-1, 1) нет такой точки, где производная f'(х) равна нулю: f'(х) = -1, если -1 < х < 0, f'(х) = 1, если 0 < х < I, а при x=0 производная f'(х) не существует.

Пример:

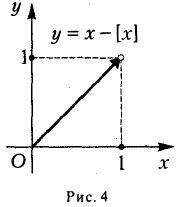
Еще пример. Функция f(х) = x — [x] (рис. 4) на отрезке [0,1 ] удовлетворяет всем условиям теоремы Ролля за исключением непрерывности: она имеет разрыв при х = 1, а производная f'(х) = 1 всюду в интервале (0, 1).

Задача:

Дана функция f(х) = I + xm(l — х)п, где m, n — целые положительные числа. Не вычисляя производной, показать, что уравнение f'(х) = 0 имеет по крайней мере один корень в интервале (0, 1).

Задача 2. Показать, что уравнение х3 + Зх — 6 = 0 имеет только один действительный корень.

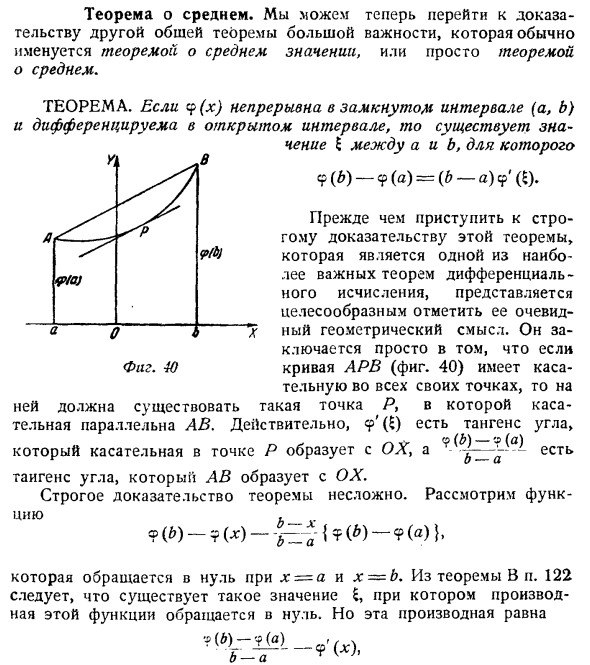
Теорема Лагранжа

Теорема:

О конечных приращениях.

Если функция f(x)

1) непрерывна на отрезке [a, b];

2) имеет производную f'{х) на интервале (а, b),

то в интервале (а, b) существует по крайней мере одна точка ξ такая, что справедлива формула

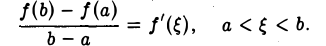
Введем вспомогательную функцию F(x), определив ее на отрезке [а, b] равенством
(1)

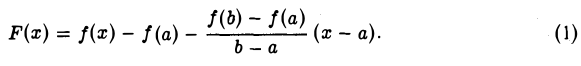
Эта функция на отрезке [а, b] удовлетворяет всем условиям теоремы Ролля. Действительно, она непрерывна на [а, b], поскольку на [а, b] непрерывно каждое слагаемое в правой части (1). На интервале (а, b) функция F(x) имеет производную, так как каждое слагаемое в выражении F(x) имеет производную на этом интервале. Наконец, непосредственной проверкой убеждаемся в том, что F(a) = F(b) = 0, т. е. F(x) принимает равные значения на концах отрезка [а, b].

В силу теоремы Ролля, существует хотя бы одна точка ξ ∈ (а, b), в которой F'(x) равна нулю,

F’ ( ξ ) = 0.

Но

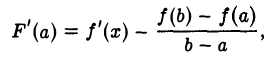
так что в точке ξ имеем

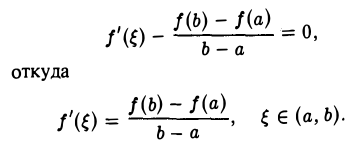
Теорема Ролля является частным случаем теоремы Лагранжа, когда f(а) = f(b).

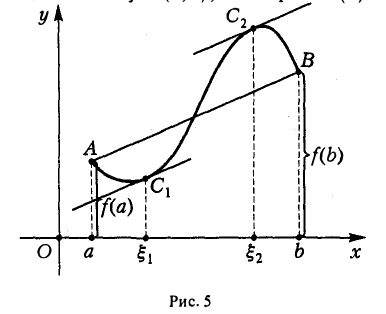
Обращаясь к геометрическому истолкованию теоремы Лагранжа, заметим, что отношение 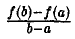Дифференциальные теоремы о среднем есть угловой коэффициент хорды АВ, а f'( ξ ) есть угловой коэффициент касательной к кривой у = f(x) в точке с абсциссой х = ξ (рис. 5). Таким образом, утверждение теоремы Лагранжа сводится к следующему: на дуге АВ непрерывной кривой, к которой можно провести касательную в любой точке, лежащей на кривой между точками A и В, всегда найдется по крайней мере одна точка С( ξ, f/( ξ )) > в которой касательная параллельна хорде АВ.

Доказанная формула 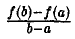Дифференциальные теоремы о среднем = f'( ξ ), или

f(b) — f(a) = f'(ξ )(b -а), а < ξ < b, (2)

носит название формулы Лагранжа или формулы конечных приращений. Она, очевидно, сохраняет силу для случая а > b.

Число ξ (вообще говоря, неизвестное, промежуточное по отношению к числам а и b) иногда удобно бывает представить в виде

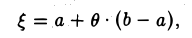
где θ — некоторое действительное число, удовлетворяющее условию 0 < θ < 1. Тогда формула Лагранжа (2) примет вид

f(b)-f(a) = f'(a + θ (b-a))(b-a), 0 < θ < 1. (3)

Взяв вместо а и b соответственно х и х + ∆х, формулу Лагранжа запишем так:

∆ f(x)=f(х + ∆ х)-f(х) = f'(х + θ > ∆ х) ∆ х, 0< θ <1. (4)

Это равенство дает точное выражение для приращения функции f(x) при любом конечном приращении ∆х аргумента, в противоположность приближенному равенству

∆f(х) = f'(х) ∆х,

относительная погрешность которого стремится к нулю лишь при ∆х → 0. Отсюда и название формулы (4) — формула конечных приращений. Отметим, что в (4) число θ, вообще говоря, неизвестно.

Пример:

Используя теорему Лагранжа, доказать справедливость неравенства

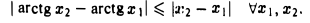
Рассмотрим функции f(х) = arctg х. Эта функция удовлетворяет всем условиям теоремы Лагранжа на любом отрезке (а, b]. Поэтому для любых х1 и x2

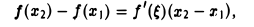
или

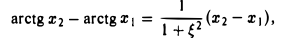
где точка ξ находится между точками х1 и х2. Отсюда

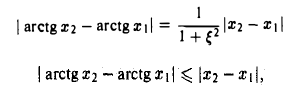
поскольку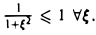 Дифференциальные теоремы о среднем

Задача:

Показать, пользуясь теоремой Лагранжа, что

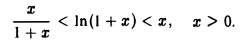
Теорема Коши осредних значениях.

Теорема Коши:

Если функции f{х) и φ(х)

1) непрерывны на отрезке [а, b];

2) имеют производные f'{х) и φ‘(х) хотя бы на интервале (а, b);

3) производная φ‘(х) ≠ 0 на интервале (а, b),

то в интервале (а, b) существует по крайней мере одна точка ξ такая, что

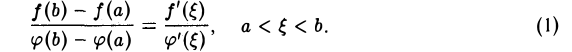
Формула (1) называется формулой Koши.

Из условия теоремы следует, что разность φ (b) — φ (a) не может равняться нулю. Действительно, если бы φ (b) — φ (а) = 0, то функция φ (х) удовлетворяла бы условиям теоремы Ролля и в таком случае φ ‘(х) была бы равна нулю по крайней мере в одной точке ξ интервала (а, b), что противоречит условию 3) теоремы Коши. Таким образом, равенство (1) имеет смысл. Покажем, что оно верно при некотором значении ξ из интервала (а, b).

Рассмотрим вспомогательную функцию

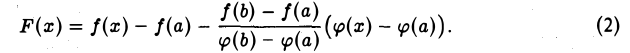
Эта функция удовлетворяет всем условиям теоремы Ролля. В самом деле:

1) F(x) непрерывна на отрезке [а, b], т.к. непрерывны на [а, b] функции f(х) и φ(х)-,

2) функция F(x) имеет производную F'(x) всюду в интервале (а, b), поскольку каждое слагаемое в правой части (2) имеет производную на этом интервале;

3) F(a) = F(b) = 0, в чем убеждаемся непосредственной проверкой. Применяя теорему Ролля, делаем вывод о существовании между а и b такой точки ξ что F'( ξ ) = 0. В силу (2)

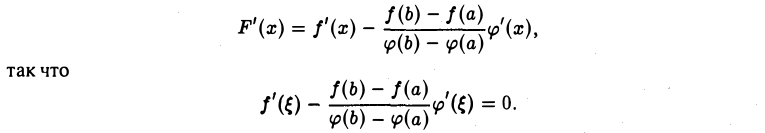
Деля все части последнего равенства на φ'( ξ ) ≠ 0, получаем требуемое равенство

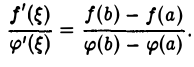
Теорема Лагранжа является частным случаем теоремы Коши: достаточно в теореме Коши взять φ(х) = х.

Задача:

Можно ли получить формулу Коши, применив к разностям f(b) — f(a) и φ(b) — φ(a) теорему Лагранжа?

Замечание:

В теоремах Ролля, Лагранжа и Коши речь идет о существовании некоторой «средней точки» ξ ∈ (а, b),для которой выполняется то или иное равенство. Поэтому вся эта группа теорем объединяется названием: теоремы о среднем дифференциального исчисления.

Раскрытие неопределенностей (правило Лопиталя)

Пусть функции f(х) и φ(х) определены в некоторой окрестности точки х = а и пусть f(а) и φ(а) = 0. Тогда отношение 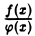Дифференциальные теоремы о среднем теряет смысл при х = а. Однако предел этого отношения в точке х = а может существовать. Задача отыскания предела 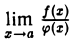в этом случае называется раскрытием неопределенности вида 0/0.

Раскрыть неопределенность вида 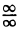Дифференциальные теоремы о среднем значит найти предел 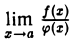при условии, что

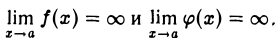
Раскрытие неопределенности вида ∞ — ∞ состоите отыскании предела 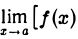Дифференциальные теоремы о среднем — φ(x)] при условии, что

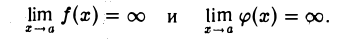
Аналогично трактуются эти понятия для случая, когда х —» ∞ .

Теорема:

Правило Лопиталя. Пусть функции f(x) и φ(х) имеют производные f'(x) и φ‘(х) в некоторой окрестности (а — δ , а + δ ) точки а, кроме, быть может, самой точки а, причем φ(x) и φ‘{х) не равны нулю в указанной окрестности. Если

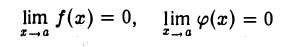
и отношение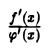 при х —» а имеет конечный или бесконечный предел, то существует и предел

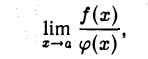
причем

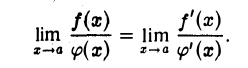
В теореме ничего не сказано о значениях f(x) и φ(x) в точке х = а. Положим f(а) = 0, φ(а) = 0. Так как теперь

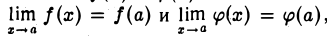
то функции f(x) и φ(x) будут непрерывны в точке а. Поэтому на отрезке [а, х] (или [х, а]),где х — какая угодно точка интервала (а — δ , а + δ), функции f(x) и φ(x) удовлетворяют всем условиям теоремы Коши. Следовательно, между а и х найдется по крайней мере одна точка ξ = ξ(х) такая, что

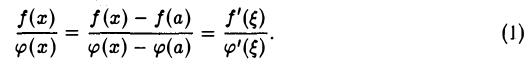
Если при некотором значении х таких точек ξ будет больше одной, то фиксируем какую-нибудь одну из них.

Величина ξ зависит от х, причем ξ → а, когда х → а. По условию при х → a отношение 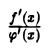Дифференциальные теоремы о среднем имеет конечный или бесконечный предел. Этот предел не зависит от способа стремления х к точке а. Поэтому при х → а, когда ξ → а, отношение 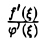Дифференциальные теоремы о среднем имеет предел, совпадающий с пределом отношения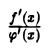

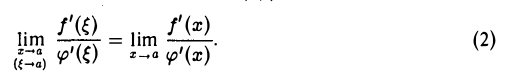
Из соотношений (1) и (2) следует, что

Равенство (3) выражает правило Лопиталя, в силу которого вычисление предела отношения функций может быть заменено (при известных условиях) вычислением предела отношения производных этих функций, что иногда бывает проще.

Пример:

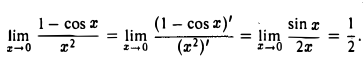
Замечание:

Если условия теоремы выполнены только в интервале (а — δ , a) или (а, а + δ ), то формулой (3) можно пользоваться для вычисления предела соответственно при х → a — 0 или z → а + 0.

Замечание:

Может оказаться, что предел отношения производных не существует, в то время как предел отношения функций существует.

Рассмотрим, например, функции f(x)= х²sin 1/x и φ(х) = х. Их отношение в точке х = 0 имеет предел

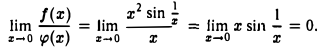
В то же время отношение производных 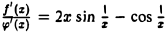Дифференциальные теоремы о среднем в точке x = 0 предела не имеет. Таким образом, из существования 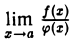не следует существования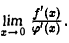

Замечание:

При вычислении 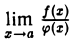Дифференциальные теоремы о среднем иногда приходится применять правило Лопиталя последовательно несколько раз. Так, если условиям теоремы Лопиталя удовлетворяют не только функции f(х) и φ(x), но и их производные f'(х) и φ'(х), то для вычисления 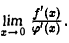Дифференциальные теоремы о среднем опять можно воспользоваться правилом Лопиталя и т. д. Пример.

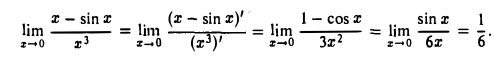
Теорема:

Второе правило Лопиталя. Пусть функции f(x) и φ(x) имеют производные f'(x) и φ'(х) в некоторой окрестности (а -δ, а +δ) точки а, кроме, быть может, самой точки а, причем φ(х) и φ'(х) не равны нулю в указанной окрестности. Если

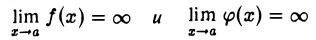
и при х → а отношение 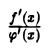Дифференциальные теоремы о среднем имеет конечный или бесконечный предел, то существует и предел 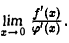, причем

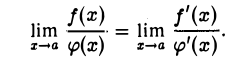
Здесь также можно рассматривать пределы при х —> а — 0 или х —> а + 0 (см. замечание 1). Пример.

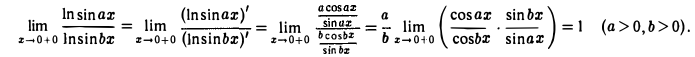
Правила Лопиталя могут быть использованы при вычислении следующих пределов:

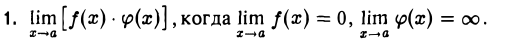
В этом случае достаточно записать выражение f(x) φ(x) в виде

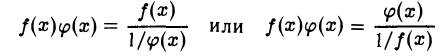
Пример:

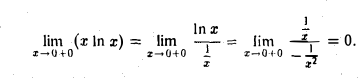
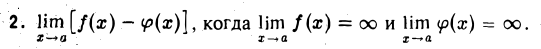
В этом случае выражение f(x) — φ(x) надо опять представить в виде частного

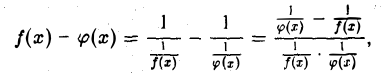
и затем воспользоваться правилом Лопиталя.

Пример:

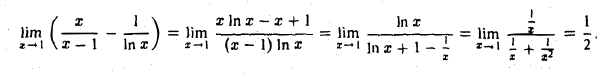
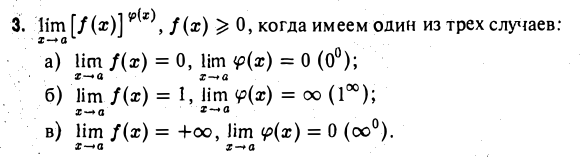
Положим

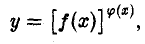
логарифмируя, получим

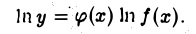
Вычислим

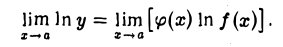
Нетрудно заметить, что для этого в каждом из указанных трех случаев а), б), в) придется вычислять предел такого вида, который рассмотрен в случае 1. Пусть мы нашли, что 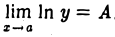Дифференциальные теоремы о среднем . Тогда

Пример:

Найти 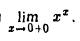Дифференциальные теоремы о среднем

Положим у = xx; тогда In у = х In x. Отсюда

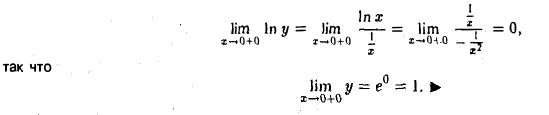
Теорема:

Пусть

1) функции f(x) и φ(х) определены для всех х, достаточно больших по абсолютной величине;

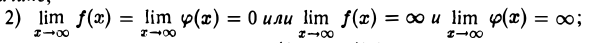
3) существуют производные /'(х) и ф'{х) ≠ 0 для всех х, достаточно больших по абсолютной величине’,

4) существует (конечный или бесконечный) предел отношения

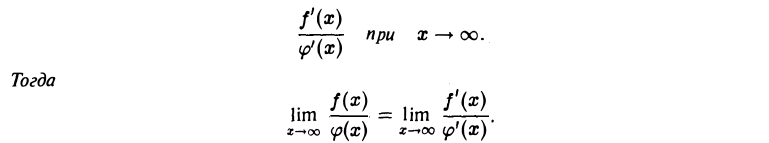
Чтобы убедиться в справедливости теоремы 6, достаточно преобразовать переменную х по формуле х = 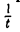Дифференциальные теоремы о среднем и воспользоваться результатами теорем 4 и 5.

Пример:

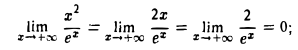
n-кратным применением правила Лопиталя вычисляется предел

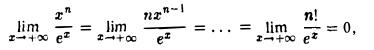
так что функция ex при x → + ∞ растет быстрее любой степени х.

Следующий пример показывает, что правило Лопиталя хотя и применимо к вычислению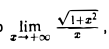 Дифференциальные теоремы о среднем но фактически бессильно. В самом деле, применяя это правило, будем иметь

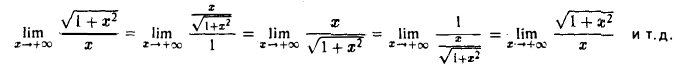
Элементарными приемами этот предел вычисляется без труда:

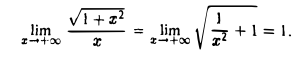
Формула Тейлора

Эта формула является одной из основных формул математического анализа и имеет многочисленные приложения.

Начнем с того, что выведем формулу Тейлора для многочлена степени п. Рассмотрим многочлен n-ой степени

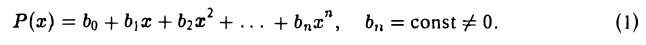
Каково бы ни было число а, многочлен (1) можно представить в виде суммы степеней разности х — а, взятых с некоторыми коэффициентами. Действительно, положим

х = а + t.

Тогда

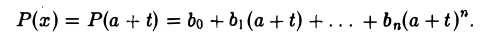
Раскрывая в правой части скобки и сгруппировав подобные члены, получим

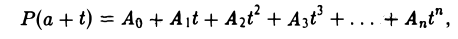
или, выразив обратно t через х,

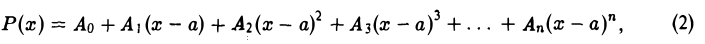
где А0, А1,…, Аn — некоторые постоянные.

Взяв многочлен Р(х) в форме (2) и продифференцировав его п раз по х, найдем

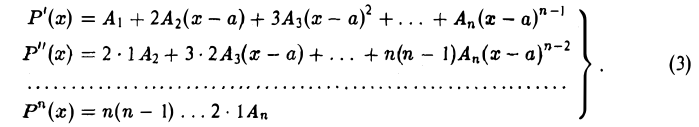
Полагая в равенствах (2) и (3) х = а, получим

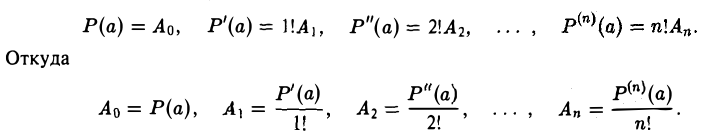
Следовательно, равенство (2) может быть записано в виде
(4)

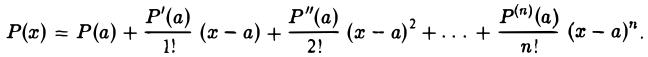
Этой есть формула Тейлора по степеням х- а для многочлена Р(х) степени п. Отсюда в частном случае при а = 0 получим формулу Маклорена
(5)

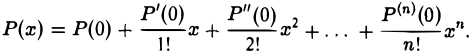
Пример:

Многочлен Р(х) = х² — 3x + 2 разложить

а) по степеням x;

б) по степеням х — 1.

а) Имеем

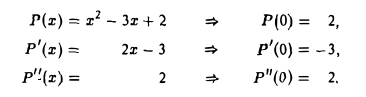
По формуле (5)

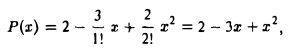
т. е. получаем исходный многочлен,

б) Имеем

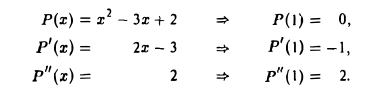
По формуле (4)

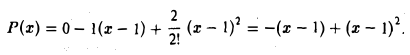
Заметим, что по формуле (4) мы можем вычислить значения многочлена Р(х) в любой точке х, если известны значения многочлена и всех его производных в одной какой-нибудь точке а.

2. Пусть теперь в окрестности точки х = а задана функция f(х), не являющаяся многочленом степени п — I, но имеющая в этой окрестности производные до п-го порядка включительно.

Вычислим величины

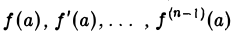
и построим функцию
(6)

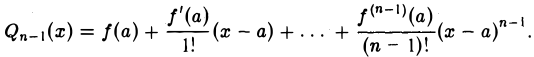
Очевидно, 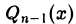Дифференциальные теоремы о среднем есть многочлен степени п — 1. Он называется многочленом Тейлора по степеням х — а для функции f{x). Если бы исходная функция f(x) сама бы была многочленом степени п — 1, то выполнялось бы тождество f(x) ≡ 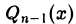Дифференциальные теоремы о среднем для всех значений х из рассматриваемой окрестности. В данном случае это тождество не имеет места, поскольку мы предположили, что f{х) не есть многочлен степени п — I. Положим (7)

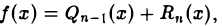
где 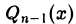Дифференциальные теоремы о среднем есть многочлен Тейлора степени п — 1 для функции f(х) по степеням х — а. Равенство (7) называется формулой Тейлора для функции f(х) в окрестности точки х = а, а Rn(x) называется остаточным членом рассматриваемой формулы Тейлора.

Для остаточного члена Rn можно дать выражение через n-ю производную от f(x). Займемся этим.

Пусть функция f(х), не являющаяся многочленом степени п — 1, на отрезке [а, b] имеет непрерывные производные до (п — 1)-го порядка включительно, а в интервале (а, b) существует и производная n-го порядка. Запишем формально равенство

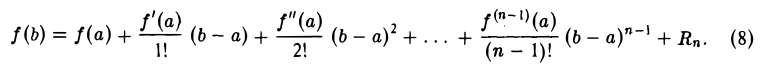
Будем искать Rn в виде

где величина М подлежит определению. С этой целью введем вспомогательную функцию φ(x), определив ее на отрезке [а, b] равенством

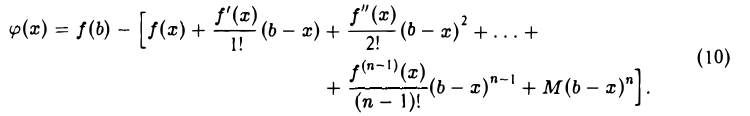
Эта функция получается, если из f(b) вычесть правую часть (8), в которой точка а заменена на х…

Функция φ(х) на отрезке [а, b] удовлетворяет всем условиям теоремы Ролля. Действительно,

1) функция φ(х) непрерывна на отрезке [a, b], потому что на этом отрезке непрерывна исходная функция f(x) вместе со своими производными до (п — 1)-го порядка включительно;

2) функция φ(x) имеет на интервале (а, b) производную, потому что на нем имеет производную n-го порядка исходная функция f(x),

3) функция φ(х) на концах отрезка [а, b] имеет равные значения: φ(а) = 0, что следует из равенства (8), и φ(b) = 0, что видно из формулы (10). Поэтому, согласно теореме Ролля, существует такая точка ξ ∈ (а, b), что φ'( ξ ) = 0.

Найдем производную φ'(х):

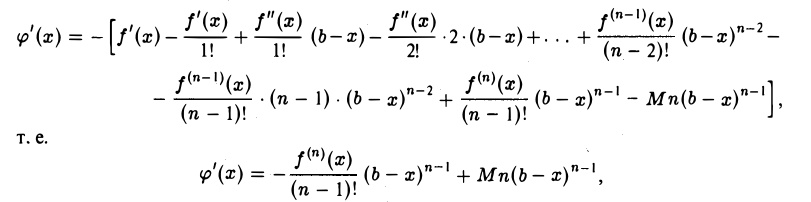
поскольку все члены сокращаются, кроме последних двух. Таким образом,

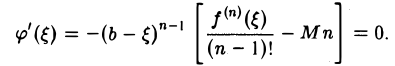
Так как ξ ≠ b (точка ξ находится в интервале (а, b)), то отсюда следует, что

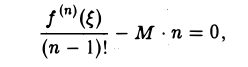
а потому М = 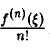Дифференциальные теоремы о среднем . Таким образом, для Rn (см. формулу (9)) получаем выражение

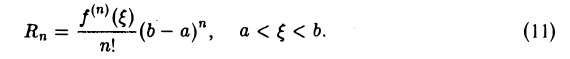
Подставляя найденное значение Rn в равенство (8), получим (12)

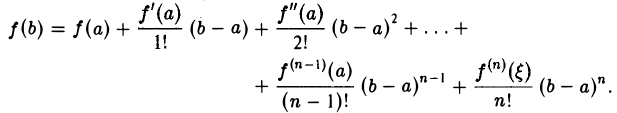
Эта формула называется формулой Тейлора для функции f(х). Последнее слагаемое правой части (12)

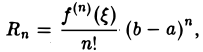
где ξ — некоторая точка, находящаяся между а и b, называется остаточным членом формулы Тейлора в форме Лагранжа.

При n = 1 из формулы Тейлора (12) получаем как частный случай формулу Лагранжа

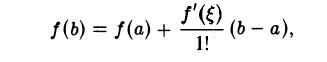
или

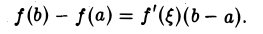
В равенстве (12) вместо а и b можно взять любые точки х0 и х из отрезка [а, b]. Поэтому формулу Тейлора для функции f(х) можно записать в виде (13)

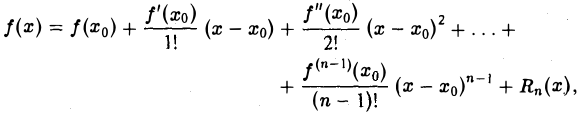
где

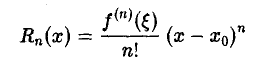
(точка ξ находится между х и х0), или

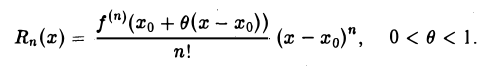
При х0 = 0 получаем формулу Маклорена (14)

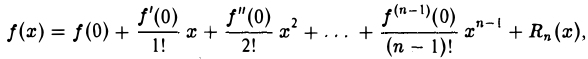
где

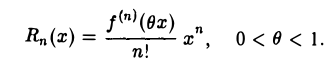
Формула Тейлора с остаточным членом в форме Пеано

Мы предполагали, что функция f(x) имеет в окрестности точки xq производную f(n)(x). Предположим теперь, что f(n)(х) непрерывнa точке хо. Тогда

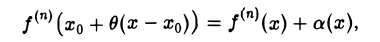
где а(х) → 0 при х → хо, и остаточный член

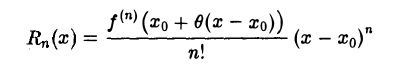
можно записать так:

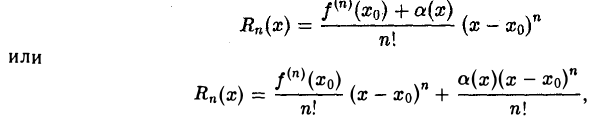
где 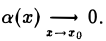Дифференциальные теоремы о среднем Так как 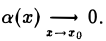, то 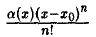есть о((х — х0)n), х → хо. Поэтому формула(13) примет вид (15)

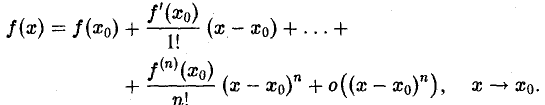
Формулу (15) называют формулой Тейлора разложения функции f(x) по степеням х — xо с остаточным членом в форме Пеано. Эта формула показывает, что, заменив f(x) в окрестности точки хо ее многочленом Тейлора n-ой степени, мы совершим ошибку, которая при х —> хо является бесконечно малой более высокого порядка, чем (x-xo)n. Следовательно, формула (15) представляет наибольший интерес при х, достаточно близких к хо. Поэтому ее называют еще локальной формулой Тейлора.

Разложение по формуле Маклорена некоторых элементарных функций

Представим формулой Маклорена

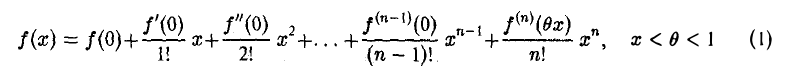
некоторые элементарные функции.

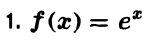
Имеем

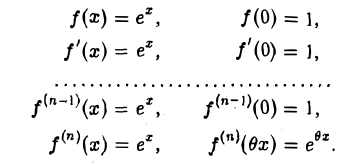
По формуле (1) будем иметь (2)

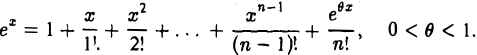
Полагая в равенстве (2) х = 1, получим (3)

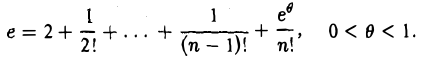
Поскольку

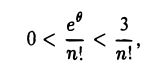
сумма

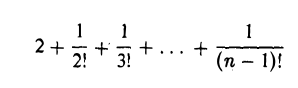
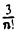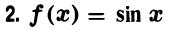
дает приближенное значение числа е с недостатком и погрешностью, меньшей Дифференциальные теоремы о среднем .

Имеем

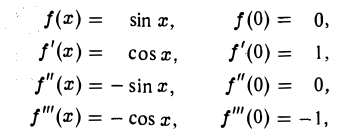
и вообще

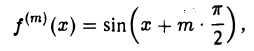
откуда

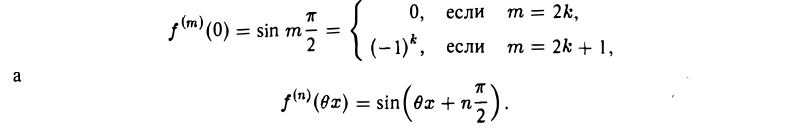
Следовательно, в многочлене Тейлора для sin х обращаются в нуль коэффициенты при четных степeнях х, так что (2n + 1)-й многочлен и (2п + 2)-й многочлен тождественны между собой.

По формуле Маклорена (1), беря п = 2к + 1, получим
(4)

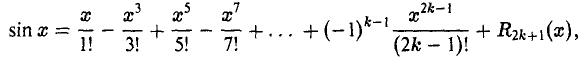
где

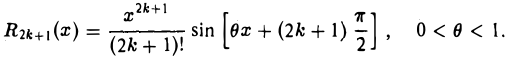
Очевидно,

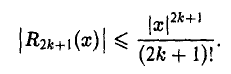
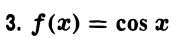
Имеем

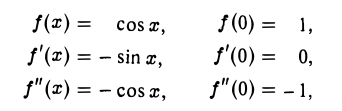
и вообще f(т)(х) = cos (х + т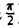 Дифференциальные теоремы о среднем ), так что

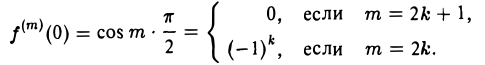
Поэтому в силу формулы (1) (если взять п = 2k + 2)
(5)

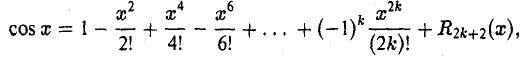
где

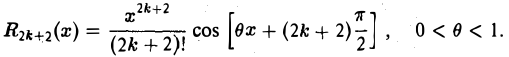
Очевидно,

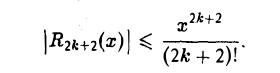
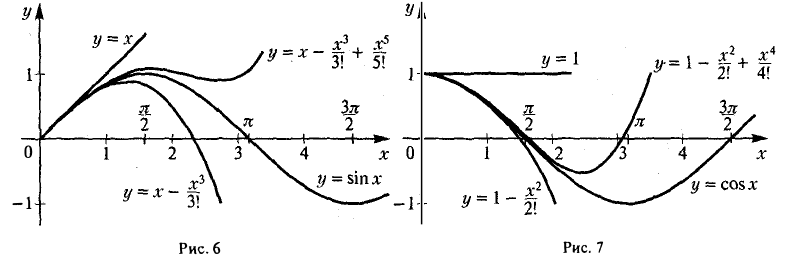
Формулами (4) и (5) можно пользоваться для вычисления приближенных значений sin х и cos x с любой степенью точности. На рис.6 и 7 показано приближение функций sin х и cos х в окрестности точки х = 0 многочленами Тейлора этих функций.

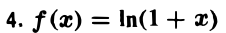
Эта функция определена и дифференцируема любое число раз для х > -1. Имеем

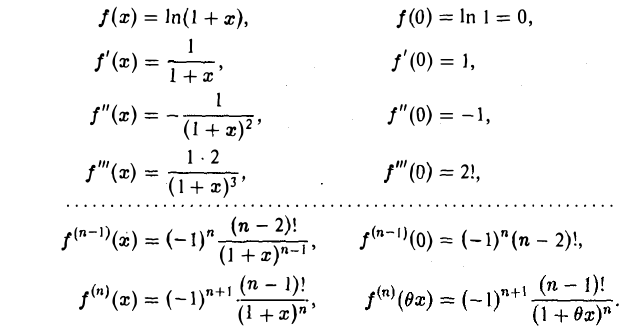
В силу формулы Маклорена (I)
(7)

где

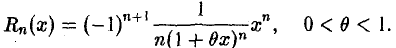
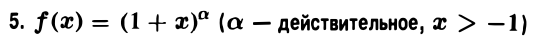
Имеем

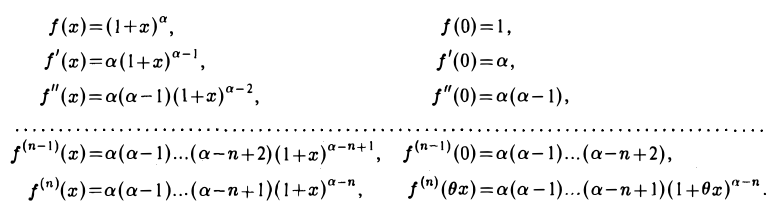
Поэтому (8)

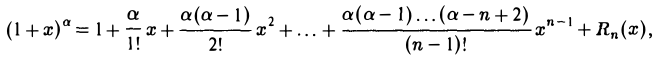
где

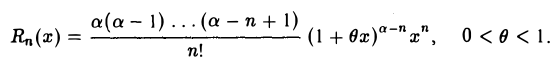
Если а = т — натуральному числу, то все члены формулы (1) начиная с (т+ 1)-го исчезают, и формула Маклорена превращается в известную формулу бинома Ньютона

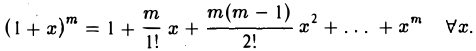
Использование формулы Маклорена для получения асимптотических оценок элементарных функций и вычисления пределов

В свое время мы установили асимптотические формулы для элементарных функций.

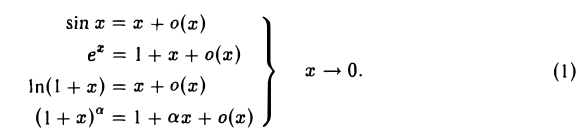
Формулы (1) дают представление элементарных функций при малых значениях |х|. Мы пользовались ими при вычислении простейших пределов. Для вычисления более тонких пределов, когда определяющую роль играют члены высокого порядка относительно х при х —> 0, формулы (1) оказываются недостаточными. Поэтому возникает необходимость получить более точные асимптотические оценки для элементарных функций. Такие оценки легко получаем из формулы Маклорена, если в этой формуле взять остаточный член в форме Пеано. Приведем эти оценки: (2)

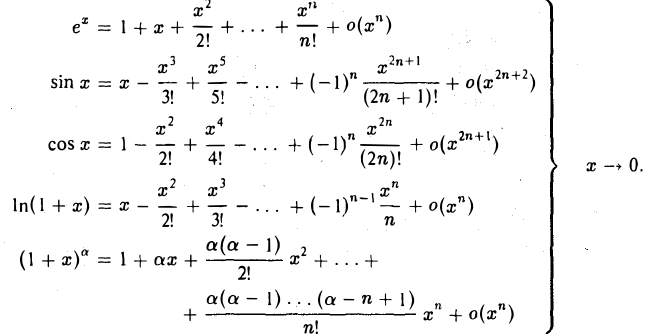
Пример:

Найти предел

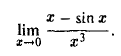
При помощи формул (I) предел этот найти невозможно, поскольку по виду знаменателя можно заключить, что определяющую роль играют члены 3-го порядка относительно х (х → 0). Поэтому воспользуемся оценками (2). Получим

Дополнение к теореме о среднем

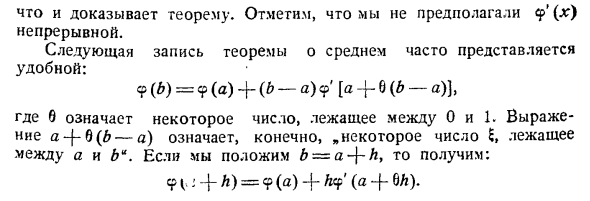
Смотрите также:

Решение задач по высшей математике

Некоторые общие теоремы, относящиеся к производным	Интегрирование
Максимумы и минимумы	Задача практического интегрирования

Решение заданий и задач по предметам:

Дополнительные лекции по высшей математике: