Оглавление:
Преобразование рационального выражения – это упрощение рационального выражения. Порядок действий при преобразовании рациональных выражений: сначала идут действия в скобках, затем операции умножения (деления), а затем уже операции сложения (вычитания).
Тождественные преобразования целых выражений
Степень с натуральным показателем
Если а— действительное число, а n — натуральное число, отличное от единицы, то произведение n сомножителей, каждый из которых равен а, называется n-й степенью числа а и обозначается 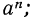 если
если 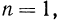 то полагают
то полагают 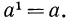 Число а называется основанием степени, число n — показателем степени.
Число а называется основанием степени, число n — показателем степени.
Например, 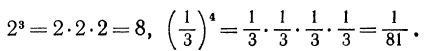
Свойства степени с натуральным показателем
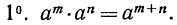
Например, 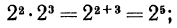
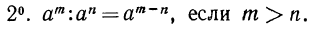
Например, 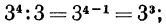
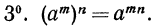
Например, 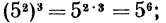
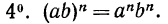
Например, 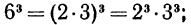
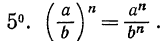
Например, 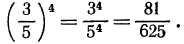
Докажем эти свойства.
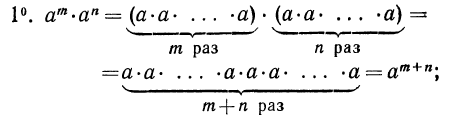
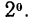 из свойства
из свойства 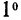 вытекает, что
вытекает, что 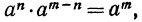 значит,
значит, 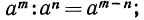

Операции над одночленами
Одночленом называется такое выражение, которое содержит числа, переменные, степени чисел и переменных и их произведения.
Например, одночленами являются выражения 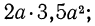
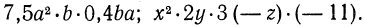 Приведем также примеры выражении, не являющихся одночленами:
Приведем также примеры выражении, не являющихся одночленами: 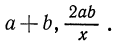
Основные законы алгебры и свойства степени с натуральным показателем позволяют нам привести одночлен к стандартному виду, т. е. к такому виду, когда одночлен имеет единственный числовой множитель, стоящий на первом месте (коэффициент), а каждое произведение одинаковых переменных в нем представлено степенью. Приведем для примера к стандартному виду данные выше одночлены. Рассмотрим первый одночлен. Воспользовавшись переместительным и сочетательным законами умножения, получим 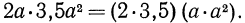 Так как
Так как 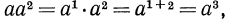 то в итоге получаем
то в итоге получаем 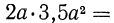
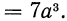 Аналогично,
Аналогично, 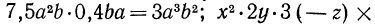
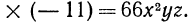
Пусть даны два одночлена. Если поставить между ними знак умножения, то получится одночлен, называемый произведением исходных одночленов. При возведении одночлена в натуральную степень также получается одночлен. Результат обычно приводят к стандартному виду.
Примеры:
Выполнить умножение одночленов 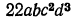 и
и 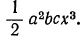
Решение. Имеем: 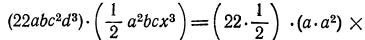
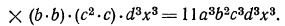
2.Возвести одночлен 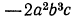 в четвертую степень.
в четвертую степень.
Решение:
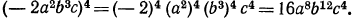
Одночлены, приведенные к стандартному виду, называются подобными, если они отличаются только коэффициентами либо совсем не отличаются.
Подобные одночлены можно складывать и вычитать, в результате чего снова получается одночлен, подобный исходным. Сложение и вычитание подобных одночленов, называется приведением подобных членов.
Пример:
Выполнить сложение одночленов 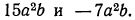
Решение:
Воспользовавшись распределительным законом, получим:
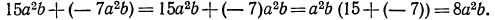
Понятие тождественного преобразования выражения
Сравним значения выражений 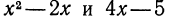 при различных значениях х. При
при различных значениях х. При 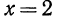 получим
получим 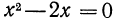 и
и 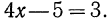 Числа 0 и 3 называются соответственными значениями выражений
Числа 0 и 3 называются соответственными значениями выражений 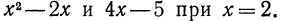
Найдем соответственные значения выражений 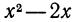 и
и 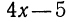 при
при 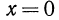 и при
и при 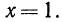 Результат запишем в виде таблицы
Результат запишем в виде таблицы
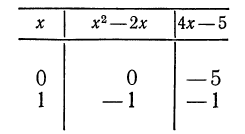
Как видно из таблицы, соответственные значения могут иногда совпадать.
Два выражения, зависящие от одних и тех же переменных, называются тождественно равными, если все их соответственные значения равны. Так, тождественно равными будут выражения 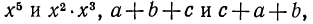
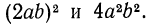
Равенство, в котором левая и правая части—тождественно равные выражения, называется тождеством. Тождествами будут, во-первых, все равенства, выражающие основные законы алгебры:
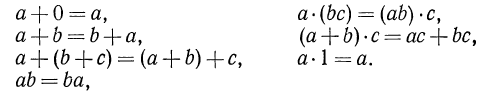
Тождествами являются и равенства 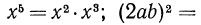
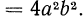
Верные числовые равенства также называются тождествами.
Замена одного выражения другим, тождественно равным ему, называется тождественным преобразованием выражения. Мы уже имели некоторые примеры тождественных преобразований. Так, приведение одночлена к стандартному виду есть тождественное преобразование, выполняемое на основании определения степени или свойств степени с натуральным показателем и перемес-тительного и сочетательного законов умножения. Тождественными преобразованиями являются также умножение одночленов и их возведение в натуральную степень, приведение подобных членов. Другие примеры тождественных преобразований выражений будут рассмотрены ниже.
Многочлены. Приведение многочлена к стандартному виду
Многочленом называется сумма одночленов. Если все члены многочлена записать в стандартном виде и выполнить приведение подобных членов, то получится многочлен стандартного вида. Например, выражение 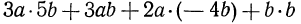 является многочленом. Для приведения его к стандартному виду нужно сначала привести к стандартному виду члены многочлена:
является многочленом. Для приведения его к стандартному виду нужно сначала привести к стандартному виду члены многочлена: 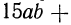
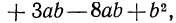 а затем привести подобные члены; тогда получим
а затем привести подобные члены; тогда получим 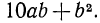
Одночлены, многочлены, а также их сумма, разность, произведение и степень составляют множество целых алгебраических выражений.
Основная задача тождественных преобразований целых выражений состоит в приведении их к стандартному виду многочлена (или одночлена). Такое преобразование всегда выполнимо.
Примеры:
Упростить (привести к стандартному виду) многочлены:
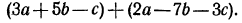
Решение:
Если перед скобками стоит знак «плюс», то скобки можно опустить, сохранив знаки всех слагаемых, заключенных в скобки. Воспользовавшись этим правилом раскрытия скобок, получим
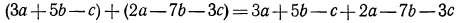
и далее
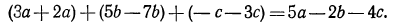
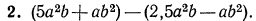
Решение:
Если перед скобками стоит знак «минус», то скобки можно опустить, изменив знаки всех слагаемых, заключенных в скобки. Воспользовавшись этим правилом раскрытия скобок, получим
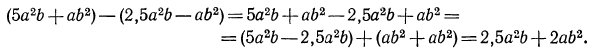
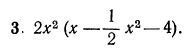
Решение:
Воспользовавшись распределительным законом 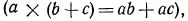
получим
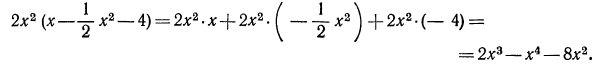
Таким образом, произведение одночлена на многочлен равно сумме произведений этого одночлена на каждый член многочлена.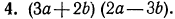
Решение:
Обозначим выражение  буквой x тогда выражение
буквой x тогда выражение 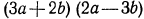 примет вид
примет вид 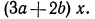 Раскрыв скобки, получим тождество
Раскрыв скобки, получим тождество
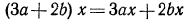
или (так как 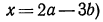
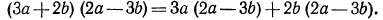
Снова раскрывая скобки, получим окончательно:
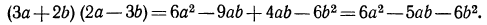
Таким образом, произведение двух многочленов равно сумме произведений каждого члена одного многочлена на каждый член другого.
Разложение многочлена на множители
Представление многочлена в виде произведения ряда многочленов, среди которых могут быть и одночлены, называется разложением многочлена на множители. Рассмотрим некоторые наиболее употребительные методы разложения многочленов на множители.
Вынесение общего множителя за скобки. Рассмотрим пример. В многочлене 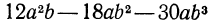 члены имеют общий множитель
члены имеют общий множитель 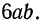 Чтобы разложить этот многочлен на множители, представим каждый член многочлена в виде произведения двух множителей, один из которых
Чтобы разложить этот многочлен на множители, представим каждый член многочлена в виде произведения двух множителей, один из которых 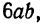 а затем применим распределительный закон:
а затем применим распределительный закон:
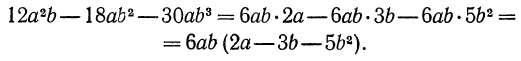
В рассмотренном примере мы вынесли за скобки 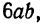 но можно было бы выполнить разложение на множители, вынося за скобки
но можно было бы выполнить разложение на множители, вынося за скобки 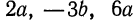 и т. д. Например, если вынести за скобки
и т. д. Например, если вынести за скобки 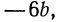 получим:
получим:
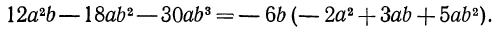
Обычно, если все коэффициенты многочлена целые числа, выносят за скобки множитель с коэффициентом, равным наибольшему общему делителю модуля всех коэффициентов многочлена. Одинаковые переменные, входящие во все члены, выносят с наименьшим показателем, который они имеют в данном многочлене.
Примеры:
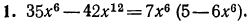
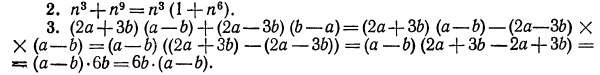
Метод группировки. Пусть дан многочлен 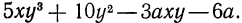
Представим его в виде суммы двух многочленов:
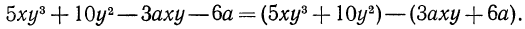
Вынося в первом двучлене за скобки 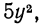 а во втором
а во втором 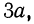 получим
получим
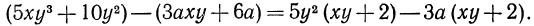
В результате проделанной группировки нам удалось представить многочлен в виде суммы двух слагаемых, имеющих общий множитель 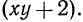 Вынося этот общий множитель за скобки, получаем
Вынося этот общий множитель за скобки, получаем
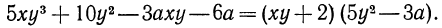
Примеры:
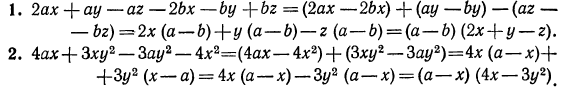
Применение тождеств сокращенного умножения. В некоторых случаях приведение многочлена к стандартному виду, а также разложение на множители производится с помощью тождеств сокращенного умножения.
А. Преобразуем выражение 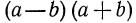 в многочлен стандартного вида. Имеем
в многочлен стандартного вида. Имеем
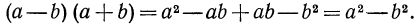
Таким образом, мы получили следующее тождество:
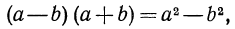
т. е. произведение суммы и разности двух выражений равно разности квадратов этих выражений.
Примеры:
Упростить, т. е. преобразовать выражение в многочлен стандартного вида:
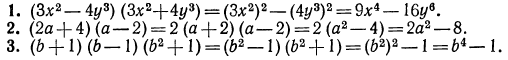
Поменяем в тождестве (1) левую и правую части местами:
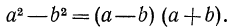
В таком виде это тождество удобно применять для разложения на множители разности квадратов двух выражений.
Примеры:
Разложить на множители:
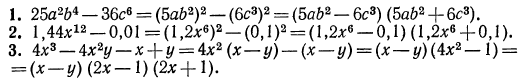
Б. Преобразуем теперь в многочлен стандартного вида выражение 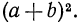 Имеем
Имеем
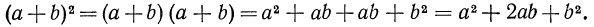
Таким образом, получено тождество
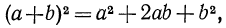
т. е. квадрат двучлена равен сумме трех выражений: квадрата первого члена, удвоенного произведения первого члена на второй и квадрата второго члена. Поменяв в тождестве (2) b на -b получим
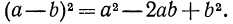
Примеры:
Упростить выражения:
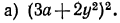
Решение:
Конечно, это выражение можно преобразовать к стандартному виду многочлена, представив его в виде 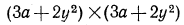 и раскрыв скобки по правилу умножения многочленов. Однако использование тождества (2) позволяет выполнить преобразования быстрее:
и раскрыв скобки по правилу умножения многочленов. Однако использование тождества (2) позволяет выполнить преобразования быстрее: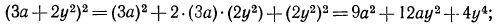
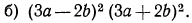
Решение:
Можно было бы возвести в квадрат каждое слагаемое, а затем результаты перемножить. Однако рациональнее сделать так:
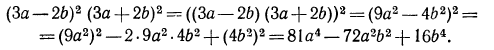
2.Доказать тождества:
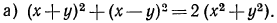
Решение:
Выполним преобразования левой части тождества:
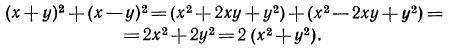
Так как в результате мы получили правую часть тождества, то тождество доказано;
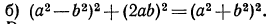
Решение:
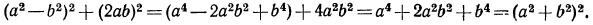
Поменяем в тождестве (2) правую и левую части местами:
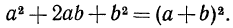
В таком виде тождество удобно применять для разложения на множители.
Примеры:
Разложить на множители:
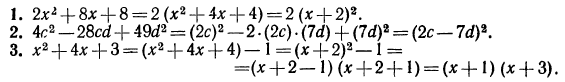
Заметим, что заданное выражение можно разложить на множители и другим способом:
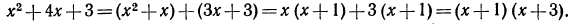
Замечание:
Мы показали, что 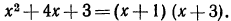 В таком случае говорят, что многочлен
В таком случае говорят, что многочлен 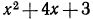 делится на
делится на 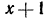 (тогда в частном получается
(тогда в частном получается 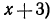 или на
или на 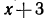 (в частном получается
(в частном получается 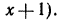
В. Рассмотрим теперь выражение 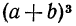 и преобразуем его в многочлен стандартного вида:
и преобразуем его в многочлен стандартного вида:
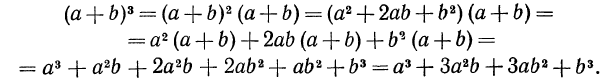
Таким образом,
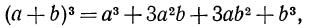
т. е. куб двучлена равен сумме четырех выражений: куба первого члена, утроенного произведения квадрата первого члена на второй, утроенного произведения первого члена на квадрат второго и куба второго члена.
Поменяв в равенстве (3) b на -b, получим
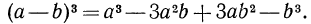
Примеры:
Преобразовать выражения в многочлен стандартного вида:
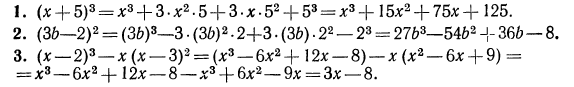
Г. Преобразуем теперь в многочлен стандартного вида выражение 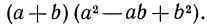 Имеем
Имеем
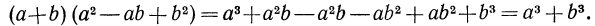
Таким образом, получено тождество
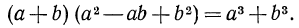
Поменяв в тождестве (4) левую и правую части, получим формулу для разложения на множители суммы кубов:
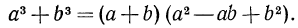
Поменяв в тождестве (4а) b на -b, получим
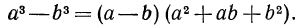
Примеры:
Упростить выражение
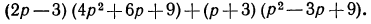
Решение:
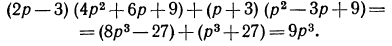
Разложить на множители 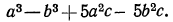
Решение:
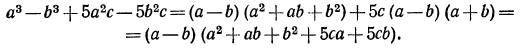
Тождественные преобразования дробных выражений
Числовые выражения, а также выражения с переменными, в которых используются операции сложения, вычитания, умножения, деления и возведения в натуральную степень, называются рациональными. Если рациональное выражение не содержит операции деления на выражение с переменными, то оно называется целым. Если же при составлении рационального выражения используется операция деления на выражение с переменными, то это рациональное выражение называется дробным.
Примеры дробных выражений:
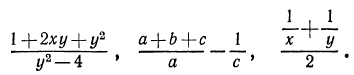
Выражение 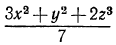 не является дробным, хотя в записи выражения и используется черта дроби. Это—целое выражение, которое можно привести к стандартному виду многочлена
не является дробным, хотя в записи выражения и используется черта дроби. Это—целое выражение, которое можно привести к стандартному виду многочлена 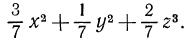
Во множестве рациональных выражений выделим еще одно подмножество выражений—подмножество дробей. Дробь — это выражение вида 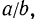 где буквами
где буквами 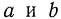 обозначены числовые выражения или выражения с переменными; а—числитель дроби, b — знаменатель. Согласно этому определению, из рассмотренных выше примеров дробями будут следующие:
обозначены числовые выражения или выражения с переменными; а—числитель дроби, b — знаменатель. Согласно этому определению, из рассмотренных выше примеров дробями будут следующие:
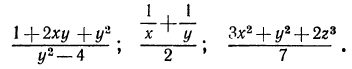
Дробное выражение 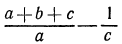 не является дробью.
не является дробью.
Обращаем внимание читателя на следующее обстоятельство: не всякая дробь является дробным выражением. Так, рассмотренное выше выражение 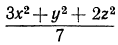 является дробью, но не является дробным выражением (нет деления на выражение с переменными).
является дробью, но не является дробным выражением (нет деления на выражение с переменными).
Одна из основных задач тождественных преобразований дробных выражений состоит в том, чтобы данное выражение представить в виде дроби, числитель и знаменатель которой—целые выражения. Чтобы выделить такие дроби из множества всех дробей, условимся называть их алгебраическими. Такое преобразование, как мы увидим, всегда выполнимо.
Областью определения выражения с одной переменной называется множество значений переменной, при которых это выражение имеет смысл. Так, область определения выражения 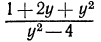 (обозначим ее Y) состоит из всех чисел, за исключением —2 и 2. Это можно записать так:
(обозначим ее Y) состоит из всех чисел, за исключением —2 и 2. Это можно записать так:
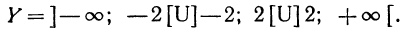
Это множество можно изобразить графически в виде числовой прямой с двумя проколотыми точками (рис. 20).
Если дано выражение с двумя переменными х и у, то областью его определения будет множество числовых пар вида 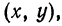 при которых выражение имеет смысл. Так, выражение
при которых выражение имеет смысл. Так, выражение 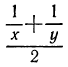 определено на множестве всех пар
определено на множестве всех пар 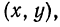 за исключением пар вида
за исключением пар вида 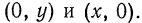 Это—множество точек координатной плоскости
Это—множество точек координатной плоскости 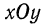 за исключением точек, лежащих на осях
за исключением точек, лежащих на осях 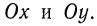
Целые выражения с переменными определены при любых значениях переменных. Если дана алгебраическая дробь, причем знаменатель содержит переменные, то чтобы найти область определения дроби, нужно найти значения переменных, при которых знаменатель обращается в ноль, и исключить такие значения.
Основное свойство дроби
Как известно, числитель и знаменатель обыкновенной дроби можно умножить или разделить на одно и то же отличное от нуля число. Например,
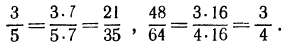
Естественным обобщением этого факта является основное свойство дроби, выражаемое тождеством
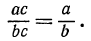
Основное свойство дроби имеет разнообразные применения. Так, если числитель и знаменатель дроби являются многочленами с дробными коэффициентами, то для упрощения записи целесообразно умножить числитель и знаменатель дроби на наименьшее общее кратное знаменателей всех коэффициентов. Это умножение является законным в силу основного свойства дроби.
Пример:
Упростить дробь 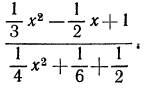
Решение:
Наименьшим общим кратным знаменателей всех коэффициентов будет в данном случае число 12. Умножив и числитель, и знаменатель дроби на 12, получим
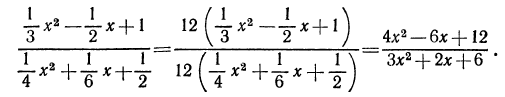
Основное свойство дроби используется для перемены знаков у членов дроби. Пусть дана дробь 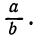 Умножив и числитель, и знаменатель дроби на (- 1), получим
Умножив и числитель, и знаменатель дроби на (- 1), получим 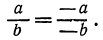
Таким образом, значение дроби не изменится, если одновременно изменить знаки у числителя и знаменателя. Если же изменить знак только у числителя или только у знаменателя, то и дробь изменит свой знак:
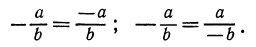
Если в последних тождествах изменить знаки левой и правой частей, то получим
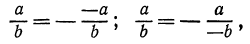
т. е. если надо изменить знак только числителя или только знаменателя дроби,то нужно изменить знак и перед самой дробью. Например,
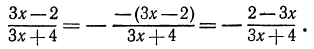
Сокращение алгебраической дроби
Сократить дробь—это значит разделить числитель и знаменатель дроби на общий множитель. Возможность такого сокращения обусловлена основным свойством дроби.
Для того чтобы сократить алгебраическую дробь, нужно числитель и знаменатель разложить на множители. Если окажется, что числитель и знаменатель имеют общие множители, то их можно сократить. Если общих множителей нет, то упрощение дроби посредством сокращения невозможно. Сокращение дроби есть тождественное преобразование.
Примеры:
Сократить дробь 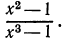
Решение:
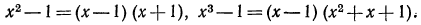
Замечаем, что числитель и знаменатель дроби имеют общий множитель  Значит надо сократить на этот общий множитель. Запись имеет такой вид:
Значит надо сократить на этот общий множитель. Запись имеет такой вид:
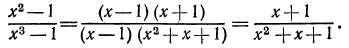
Заметим, что области определения дробей 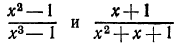 различны. Дробь
различны. Дробь 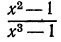 определена при
определена при 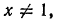 а дробь
а дробь 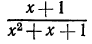 определена при любых значениях х.
определена при любых значениях х.
Значит, в результате сокращения получилась дробь, область определения которой (обозначим ее 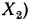 шире, чем область определения исходной дроби (обозначим ее
шире, чем область определения исходной дроби (обозначим ее 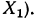 Это можно записать так:
Это можно записать так:
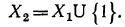
2.Сократить дробь 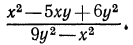
Для разложения числителя на множители применим способ группировки, представив предварительно одночлен 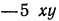 в виде суммы
в виде суммы 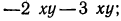 тогда
тогда
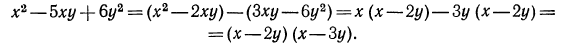
Для разложения знаменателя на множители используем формулу разности квадратов: 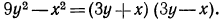
Теперь имеем:
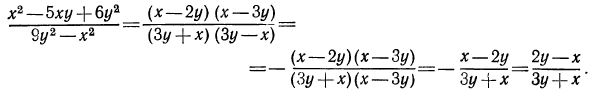
Приведение алгебраических дробей к общему знаменателю
Общим знаменателем нескольких алгебраических дробей называется многочлен, который делится на знаменатель каждой дроби. Например, общим знаменателем дробей 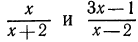 служит многочлен
служит многочлен 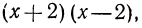 так как он делится и на
так как он делится и на 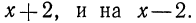 Следует, однако, заметить, что это не единственное решение поставленной задачи: общим знаменателем данных дробей будет и многочлен
Следует, однако, заметить, что это не единственное решение поставленной задачи: общим знаменателем данных дробей будет и многочлен 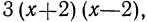 и многочлен
и многочлен 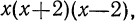 и многочлен
и многочлен 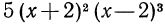 и т. д. Обычно берут такой общий знаменатель, что любой другой общий знаменатель делится на выбранный без остатка. Такой знаменатель называется наименьшим общим знаменателем (НОЗ). В рассмотренном выше примере НОЗ равен
и т. д. Обычно берут такой общий знаменатель, что любой другой общий знаменатель делится на выбранный без остатка. Такой знаменатель называется наименьшим общим знаменателем (НОЗ). В рассмотренном выше примере НОЗ равен 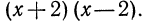
Привести дроби к наименьшему общему знаменателю— это значит преобразовать каждую из дробей к такому виду, чтобы знаменателем служил НОЗ. Возможность такого преобразования вытекает из основного свойства дроби, позволяющего умножать числитель и знаменатель дроби на один и тот же многочлен. Так, для рассмотренных выше дробей имеем
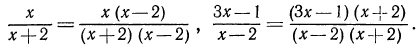
Нам удалось привести дроби к НОЗ. Это достигнуто путем умножения числителя и знаменателя первой дроби на 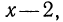 а числителя и знаменателя второй дроби на
а числителя и знаменателя второй дроби на 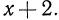 Многочлены
Многочлены 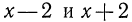 называются дополнительными множителями соответственно для первой и для второй дроби. Нетрудно понять, что дополнительный множитель для данной дроби равен частному от деления НОЗ на знаменатель данной дроби.
называются дополнительными множителями соответственно для первой и для второй дроби. Нетрудно понять, что дополнительный множитель для данной дроби равен частному от деления НОЗ на знаменатель данной дроби.
Заметим, что области определения дробей 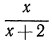 и
и 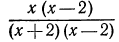 Различны. Дробь
Различны. Дробь 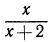 определена при
определена при 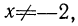 а дробь
а дробь 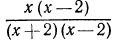 определена при значениях х, отличных от -2 и 2.
определена при значениях х, отличных от -2 и 2.
Значит, в результате умножения числителя и знаменателя дроби 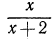 на дополнительный множитель
на дополнительный множитель 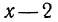 получилась дробь, область определения которой
получилась дробь, область определения которой 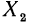 уже, чем область определения
уже, чем область определения 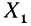 исходной дроби. Это можно записать так:
исходной дроби. Это можно записать так:
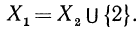
Пример:
Привести к НОЗ дроби 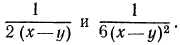
Решение:
В данном случае НОЗ равен 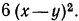 Чтобы переписать данные дроби со знаменателем
Чтобы переписать данные дроби со знаменателем 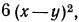 надо найти дополнительные множители. Для первой дроби дополнительным множителем будет
надо найти дополнительные множители. Для первой дроби дополнительным множителем будет 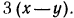 Что касается второй дроби, то ее знаменатель совпадает с НОЗ. В таком случае говорят, что дополнительный множитель равен 1. Итак,
Что касается второй дроби, то ее знаменатель совпадает с НОЗ. В таком случае говорят, что дополнительный множитель равен 1. Итак,
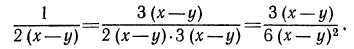
Вторую дробь оставим без изменения.
Дроби приведены к наименьшему общему знаменателю.
В общем случае, чтобы привести дроби к НОЗ, нужно все знаменатели разложить на множители, из первого знаменателя взять все множители, а из остальных добавить те, которых нет в первом. Покажем на примерах, как это делается.
Пример:
Привести к НОЗ дроби
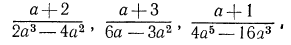
Решение:
Разложим каждый из знаменателей на множители:
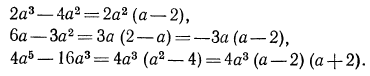
Составим НОЗ. Для зтого возьмем первый знаменатель 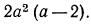 Из второго знаменателя возьмем множитель 3, ибо его нет в первом знаменателе, а из третьего знаменателя возьмем множитель
Из второго знаменателя возьмем множитель 3, ибо его нет в первом знаменателе, а из третьего знаменателя возьмем множитель 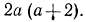 В итоге НОЗ равен
В итоге НОЗ равен 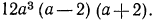
Теперь найдем дополнительные множители. Разделив НОЗ на знаменатель первой дроби, получим дополнительный множитель для первой дроби: 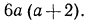 Разделив НОЗ на знаменатель второй дроби, получим дополнительный множитель для второй дроби:
Разделив НОЗ на знаменатель второй дроби, получим дополнительный множитель для второй дроби: 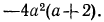 Разделив НОЗ на знаменатель третьей дроби, получим дополнительный множитель для третьей дроби: 3. Теперь имеем:
Разделив НОЗ на знаменатель третьей дроби, получим дополнительный множитель для третьей дроби: 3. Теперь имеем:
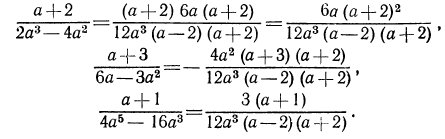
Рекомендуем придерживаться следующей схемы отыскания НОЗ и дополнительных множителей (приводим ее на базе рассмотренного примера).
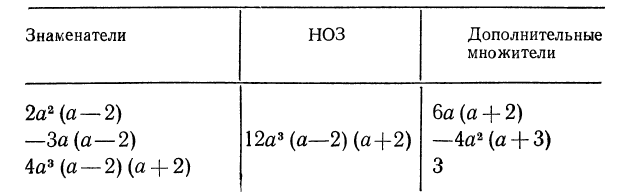
Пример:
Привести к наименьшему общему знаменателю дроби
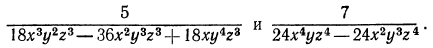
Решение:
Прежде всего разложим знаменатели на множители:
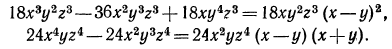
Применим схему отыскания НОЗ и дополнительных множителей.
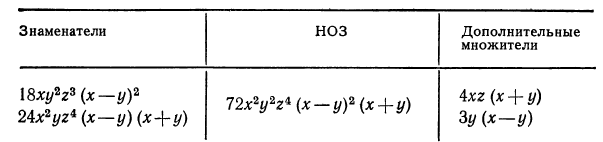
Если мы теперь числитель и знаменатель первой из данных дробей умножим на первый дополнительный множитель, а числитель и знаменатель второй дроби —на второй дополнительный множитель, то получим дроби с общим знаменателем:
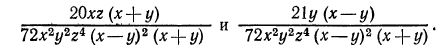
Умножение и деление алгебраических дробей
Обыкновенные дроби перемножаются следующим образом:
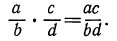
Обобщением этого равенства является тождество
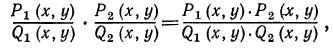
где 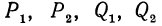 — целые алгебраические выражения. Итак, произведение двух (и вообще любого числа) алгебраических дробей тождественно равно дроби, числитель которой равен произведению числителей, а знаменатель— произведению знаменателей перемножаемых дробей.
— целые алгебраические выражения. Итак, произведение двух (и вообще любого числа) алгебраических дробей тождественно равно дроби, числитель которой равен произведению числителей, а знаменатель— произведению знаменателей перемножаемых дробей.
Деление обыкновенных дробей выполняется следующим образом:
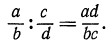
Обобщением этого равенства является тождество
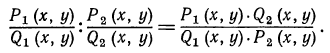
Значит, частное от деления двух алгебраических дробей тождественно равно дроби, числитель которой равен произведению числителя первой дроби на знаменатель второй дроби, а знаменатель — произведению знаменателя первой дроби на числитель второй.
Примеры:
Преобразовать в дробь произведение
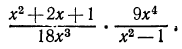
Решение:
Применяем правило умножения, затем выполняем необходимые сокращения:
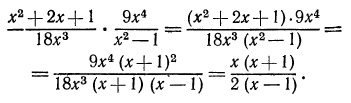
Преобразовать в дробь частное
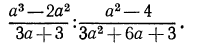
Решение:
Используем правило деления и выполняем сокращения:
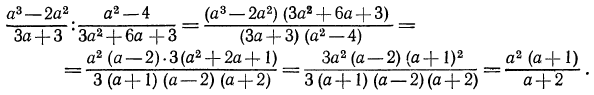
Замечания:
Учитывая возможность сокращения алгебраической дроби, получаемой в результате умножения или деления алгебраических дробей, обычно стремятся до выполнения этих операций разложить на множители числители и знаменатели исходных дробей.
2.Сформулированные правила умножения и деления распространяются и на случай умножения или деления на многочлен, достаточно записать этот многочлен в виде дроби со знаменателем 1.
Возведение алгебраической дроби в натуральную степень
Рассмотрим выражение 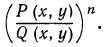 Имеем
Имеем
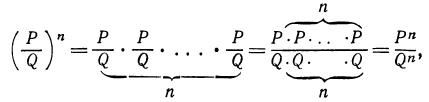
поэтому
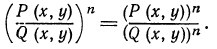
Значит, степень дроби тождественно равна дроби, у которой числитель есть степень числителя, а знаменатель —степень знаменателя.
Пример:
Преобразовать в дробь степень 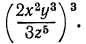
Решение:
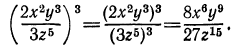
Сложение и вычитание алгебраических дробей
Для обыкновенных дробей справедливо равенство
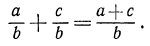
Обобщением этого равенства является тождество
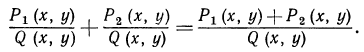
Оно означает, что сумма двух (и вообще любого числа) алгебраических дробей с одинаковым знаменателем тождественно равна алгебраической дроби с тем же знаменателем и с числителем, равным сумме числителей складываемых дробей.
Аналогично обстоит дело в случае вычитания дробей с одинаковым знаменателем. В самом деле,
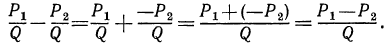
Пример:
Преобразовать сумму 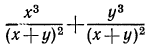 в дробь.
в дробь.
Решение:
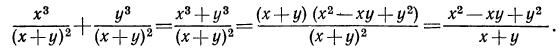
Для сложения и вычитания алгебраических дробей с разными знаменателями нужно прежде всего привести дроби к наименьшему общему знаменателю, а затем выполнить операции над полученными дробями с одинаковым знаменателем.
Примеры:
Упростить, т. е. преобразовать в дробь, выражение
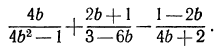
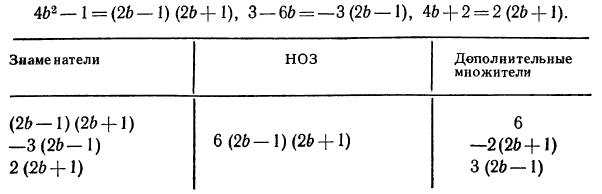
Перепишем теперь заданную алгебраическую сумму дробей с указанием дополнительных множителей, при помощи которых дроби приводятся к общему знаменателю:
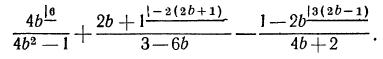
Обычно, соответствующие умножения на дополнительные множители опускают и сразу выписывают дробь, знаменателем которой является НОЗ, а числитель представляет собой сумму произведений числителей исходных дробей на соответствующие дополнительные множители, т. е.
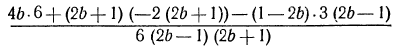
и далее,
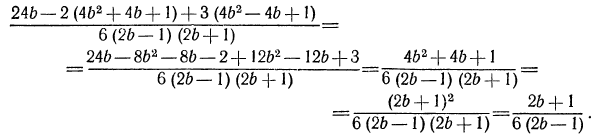
Упростить выражение 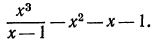
Решение:
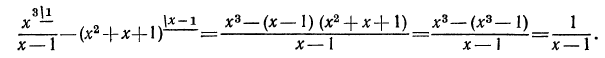
Примеры на все действия с алгебраическими дробями
1.Упростить выражение
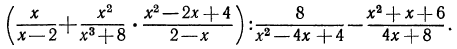
Решение:
При выполнении операций над алгебраическими дробями придерживаются того же порядка, который принят для упрощения числовых выражений, а именно: умножение, деление и возведение в степень предшествуют сложению и вычитанию; при наличии скобок прежде всего выполняют действия в скобках. В данном примере порядок действий таков:
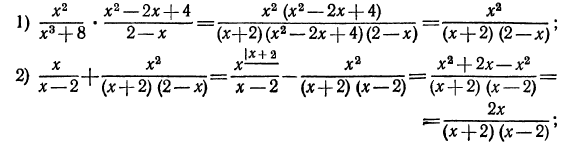
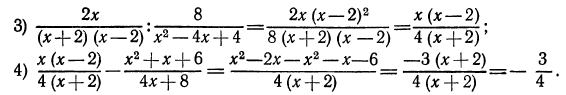
2.Упростить выражение
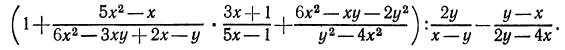
Решение:
Первым по счету действием является здесь умножение. Мы уже говорили, что умножению (и делению) обычно предшествует разложение числителей и знаменателей на множители. Имеем:
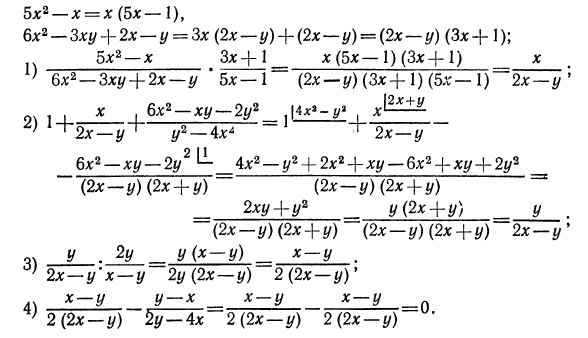
Решение заданий и задач по предметам:
Дополнительные лекции по высшей математике:
- Тождественные преобразования алгебраических выражений
- Функции и графики
- Преобразования графиков функций
- Квадратная функция и её графики
- Алгебраические неравенства
- Неравенства
- Неравенства с переменными
- Прогрессии в математике
- Арифметическая прогрессия
- Геометрическая прогрессия
- Показатели в математике
- Логарифмы в математике
- Исследование уравнений
- Уравнения высших степеней
- Уравнения высших степеней с одним неизвестным
- Комплексные числа
- Непрерывная дробь (цепная дробь)
- Алгебраические уравнения
- Неопределенные уравнения
- Соединения
- Бином Ньютона
- Число е
- Непрерывные дроби
- Функция
- Исследование функций
- Предел
- Интеграл
- Двойной интеграл
- Тройной интеграл
- Интегрирование
- Неопределённый интеграл
- Определенный интеграл
- Криволинейные интегралы
- Поверхностные интегралы
- Несобственные интегралы
- Кратные интегралы
- Интегралы, зависящие от параметра
- Квадратный трехчлен
- Производная
- Применение производной к исследованию функций
- Приложения производной
- Дифференциал функции
- Дифференцирование в математике
- Формулы и правила дифференцирования
- Дифференциальное исчисление
- Дифференциальные уравнения
- Дифференциальные уравнения первого порядка
- Дифференциальные уравнения высших порядков
- Дифференциальные уравнения в частных производных
- Тригонометрические функции
- Тригонометрические уравнения и неравенства
- Показательная функция
- Показательные уравнения
- Обобщенная степень
- Взаимно обратные функции
- Логарифмическая функция
- Уравнения и неравенства
- Положительные и отрицательные числа
- Алгебраические выражения
- Иррациональные алгебраические выражения
- Преобразование алгебраических выражений
- Преобразование дробных алгебраических выражений
- Разложение многочленов на множители
- Многочлены от одного переменного
- Алгебраические дроби
- Пропорции
- Уравнения
- Системы уравнений
- Системы уравнений высших степеней
- Системы алгебраических уравнений
- Системы линейных уравнений
- Системы дифференциальных уравнений
- Арифметический квадратный корень
- Квадратные и кубические корни
- Извлечение квадратного корня
- Рациональные числа
- Иррациональные числа
- Арифметический корень
- Квадратные уравнения
- Иррациональные уравнения
- Последовательность
- Ряды сходящиеся и расходящиеся
- Тригонометрические функции произвольного угла
- Тригонометрические формулы
- Обратные тригонометрические функции
- Теорема Безу
- Математическая индукция
- Показатель степени
- Показательные функции и логарифмы
- Множество
- Множество действительных чисел
- Числовые множества
- Преобразование иррациональных выражений
- Геометрия
- Действительные числа
- Степени и корни
- Степень с рациональным показателем
- Тригонометрические функции угла
- Тригонометрические функции числового аргумента
- Тригонометрические выражения и их преобразования
- Преобразование тригонометрических выражений
- Комбинаторика
- Вычислительная математика
- Прямая линия на плоскости и ее уравнения
- Прямая и плоскость
- Линии и уравнения
- Прямая линия
- Уравнения прямой и плоскости в пространстве
- Кривые второго порядка
- Кривые и поверхности второго порядка
- Числовые ряды
- Степенные ряды
- Ряды Фурье
- Преобразование Фурье
- Функциональные ряды
- Функции многих переменных
- Метод координат
- Гармонический анализ
- Вещественные числа
- Предел последовательности
- Аналитическая геометрия
- Аналитическая геометрия на плоскости
- Аналитическая геометрия в пространстве
- Функции одной переменной
- Высшая алгебра
- Векторная алгебра
- Векторный анализ
- Векторы
- Скалярное произведение векторов
- Векторное произведение векторов
- Смешанное произведение векторов
- Операции над векторами
- Непрерывность функций
- Предел и непрерывность функций нескольких переменных
- Предел и непрерывность функции одной переменной
- Производные и дифференциалы функции одной переменной
- Частные производные и дифференцируемость функций нескольких переменных
- Дифференциальное исчисление функции одной переменной
- Матрицы
- Линейные и евклидовы пространства
- Линейные отображения
- Дифференциальные теоремы о среднем
- Теория устойчивости дифференциальных уравнений
- Функции комплексного переменного
- Преобразование Лапласа
- Теории поля
- Операционное исчисление
- Системы координат
- Рациональная функция
- Интегральное исчисление
- Интегральное исчисление функций одной переменной
- Дифференциальное исчисление функций нескольких переменных
- Отношение в математике
- Математическая логика
- Графы в математике
- Линейные пространства
- Первообразная и неопределенный интеграл
- Линейная функция
- Выпуклые множества точек
- Система координат
