Оглавление:
Тригонометрические функции любого угла и определение синуса, косинуса, тангенса и котангенса:
Отметим на оси х справа от начала координат точку А и проведем через нее окружность с центром в точке О (рис. 64). Радиус OA будем называть начальным радиусом.
Повернем начальный радиус около точки О на 70° против часовой стрелки. При этом он перейдет в радиус ОВ. Говорят, что угол поворота равен 70°. Если повернуть начальный радиус около точки О на 70° по часовой стрелке, то он перейдет в радиус ОС. В этом случае говорят, что угол поворота равен —70°. Углы поворота в 70° и —70° показаны стрелками на рисунке 64.
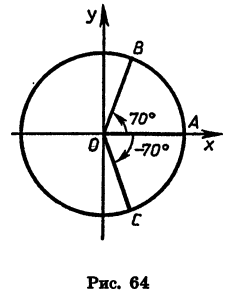
Вообще при повороте против часовой стрелки угол поворота считают положительным, а при повороте по часовой стрелке — отрицательным.
Из курса геометрии известно, что мера угла в градусах выражается числом от 0 до 180. Что касается угла поворота, то он может выражаться в градусах каким угодно действительным числом от  Так, если начальный
Так, если начальный
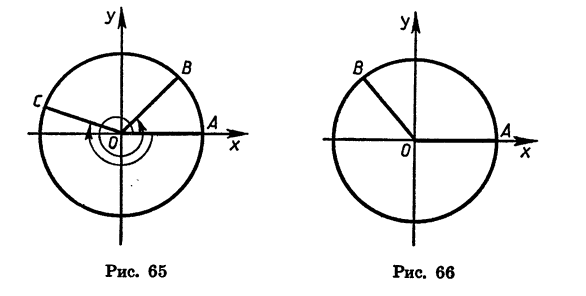
радиус повернуть против часовой стрелки на 180°, а потом еще на 30°, то угол поворота будет равен 210°. Если начальный радиус сделает полный оборот против часовой стрелки, то угол поворота будет равен 360°; если он сделает полтора оборота в том же направлении, то угол поворота будет равен 540° и т. д. На рисунке 65 стрелками показаны углы поворота в 405° и -200°.
Рассмотрим радиусы OA и ОВ (рис. 66). Существует бесконечно много углов поворота, при которых начальный радиус OA переходит в радиус ОВ. Так, если 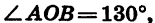 то соответствующие углы поворота будут равны 130° + 360°n, где n — любое целое число. Например, при n = 0, 1, —1, 2, —2 получаем углы поворота 130°, 490°, —230°, 850°, —590°.
то соответствующие углы поворота будут равны 130° + 360°n, где n — любое целое число. Например, при n = 0, 1, —1, 2, —2 получаем углы поворота 130°, 490°, —230°, 850°, —590°.
Пусть при повороте на угол а начальный радиус OA переходит в радиус ОВ. В зависимости от того, в какой координатной четверти окажется радиус ОВ, угол а называют углом этой четверти. Так, если 0° < а < 90°, то а — угол I четверти; если 90° < а <180°, то а — угол II четверти; если 180° < а < 270°, то а — угол III четверти; если 270° < а < 360°, то а — угол IV четверти. Очевидно, что при прибавлении к углу целого числа оборотов получается угол той же четверти. Например, угол в 430° является углом I четверти, так как 430° = 360°+ 70° и 0°<70°<90°; угол в 920° является углом III четверти, так как 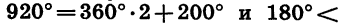 200° < 270°.
200° < 270°.
Углы 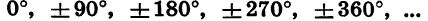 не относятся ни к какой четверти.
не относятся ни к какой четверти.
В курсе геометрии были определены синус, косинус и тангенс угла а при 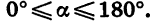 Теперь мы распространим эти определения на случай произвольного угла а. Кроме того, определим еще котангенс угла а, который обозначают ctg а.
Теперь мы распространим эти определения на случай произвольного угла а. Кроме того, определим еще котангенс угла а, который обозначают ctg а.
Пусть при повороте около точки О на угол а начальный радиус OA переходит в радиус ОВ (рис. 67).
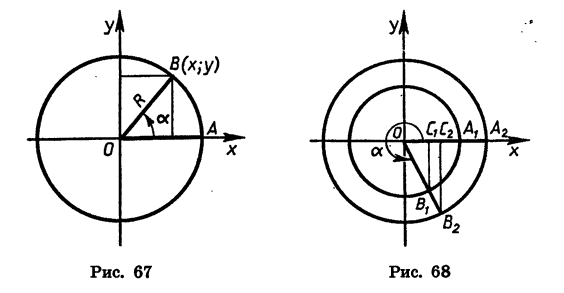
Синусом угла а называется отношение ординаты точки В к длине радиуса.
Косинусом утла а называется отношение абсциссы точки В к длине радиуса.
Тангенсом угла а называется отношение ординаты точки В к ее абсциссе.
Котангенсом угла а называется отношение абсциссы точки В к ее ординате.
Если координаты точки В равны х и у, а длина начального радиуса равна R, то
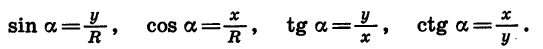
В курсе геометрии было показано, что значения синуса, косинуса и тангенса угла а, где 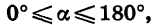 зависят только от а и не зависят от длины радиуса R. И в общем случае sin а, cos a, tg а, а также ctg а зависят только от угла а.
зависят только от а и не зависят от длины радиуса R. И в общем случае sin а, cos a, tg а, а также ctg а зависят только от угла а.
Покажем, например, что sin а не зависит от R.
Пусть при повороте луча  около точки О на угол а (рис. 68) радиусы
около точки О на угол а (рис. 68) радиусы  займут положения
займут положения 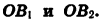 Обозначим координаты точки
Обозначим координаты точки 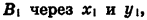 а координаты точки
а координаты точки 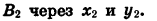
Опустим перпендикуляры из точек 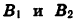 на ось х. Прямоугольные треугольники
на ось х. Прямоугольные треугольники 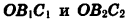 подобны. Отсюда
подобны. Отсюда
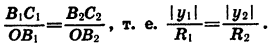
Так как точки 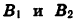 принадлежат одной и той же координатной четверти, то их ординаты
принадлежат одной и той же координатной четверти, то их ординаты 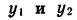 имеют одинаковые знаки. Поэтому
имеют одинаковые знаки. Поэтому 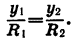
Заметим, что это равенство верно и в том случае, когда точки 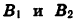 попадают на одну из осей координат. Таким образом, для любого угла а отношение
попадают на одну из осей координат. Таким образом, для любого угла а отношение 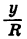 не зависит от длины радиуса R.
не зависит от длины радиуса R.
Выражения sin а и cos а определены при любом а, так как для любого угла поворота можно найти соответствующие значения дробей 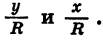 Выражение tg а имеет смысл при любом а, кроме углов поворота
Выражение tg а имеет смысл при любом а, кроме углов поворота 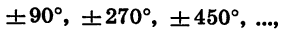 так как для этих углов не имеет смысла дробь
так как для этих углов не имеет смысла дробь 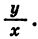 Для выражения ctg а исключаются углы 0°, ±180°, ±360°, для которых не имеет смысла дробь
Для выражения ctg а исключаются углы 0°, ±180°, ±360°, для которых не имеет смысла дробь 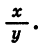
Каждому допустимому значению а соответствует единственное значение sin a, cos а, tg а и ctg а. Поэтому синус, косинус, тангенс и котангенс являются функциями угла а. Их называют тригонометрическими функциями.
Можно доказать, что областью значений синуса и косинуса является промежуток [—1; 1], а областью значений тангенса и котангенса — множество всех действительных чисел.
Приведем примеры вычисления значений тригонометрических функций.
Пример:
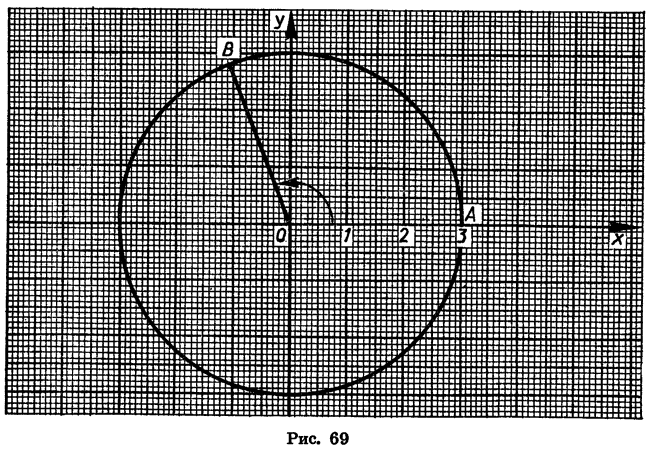
Найдем с помощью чертежа приближенные значения sin 110°, cos 110°, tg 110° и ctg 110°.
Начертим окружность с центром в начале координат и радиусом OA = R = 3 (рис. 69). Повернем радиус OA на 110°. Получим радиус ОВ. Найдем по рисунку координаты х и у точки В: 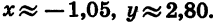 Отсюда
Отсюда
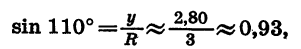
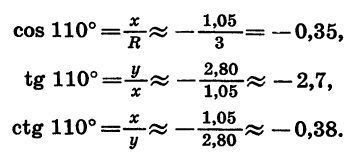
В таблице приведены известные из курса геометрии значения синуса, косинуса и тангенса углов 0°, 30°, 45°, 60° и 90°. Прочерк сделан в том случае, когда выражение не имеет смысла.
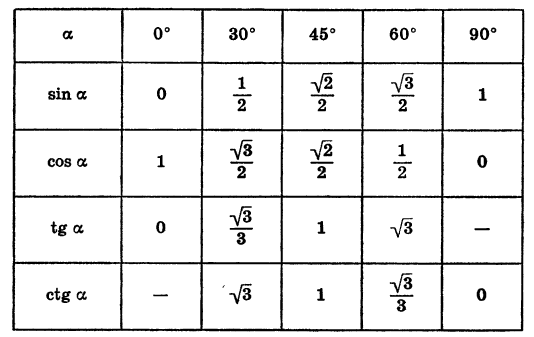
Значения котангенса могут быть получены из значений тангенса, так как котангенс угла является числом, обратным тангенсу этого же угла. Поэтому, например,
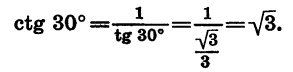
Пример:
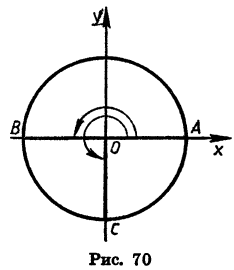
Найдем синус, косинус, тангенс и котангенс углов 180° и 270°.
При повороте на 180° около точки О радиус OA, равный 1, (рис. 70) переходит в радиус ОВ, а при повороте на 270° — в радиус ОС.
Так как точка В имеет координаты х = — 1 и у = 0, то
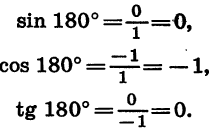
Так как точка С имеет координаты х = 0 и у = —1, то

Напомним, что выражения ctg 180° и tg 270° не имеют смысла.
Свойства синуса, косинуса, тангенса и котангенса
Рассмотрим некоторые свойства тригонометрических функций.
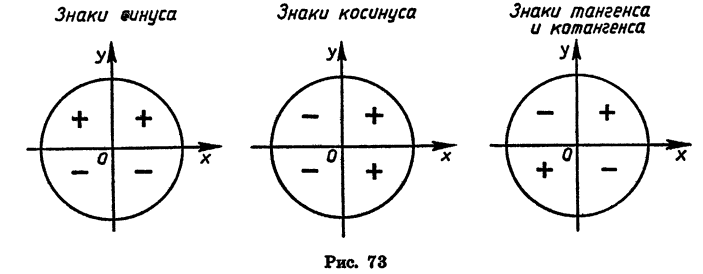
Выясним сначала, какие знаки имеют синус, косинус, тангенс и котангенс в каждой из координатных четвертей.
Пусть при повороте радиуса OA, равного R, на угол а точка А перешла в точку В с координатами х и у (см. рис. 67).
Так как 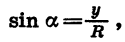 то знак sin а зависит от знака у.
то знак sin а зависит от знака у.
В I и II четвертях у > 0, а в III и IV четвертях у < 0. Значит, sin a > 0, если а является углом I или II четверти, и sin a < 0, если а является углом III или IV четверти.
Знак cos а зависит от знака х, так как 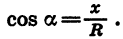 В I и IV четвертях х > 0, а во II и III четвертях х < 0. Поэтому cos a > 0, если а является углом I или IV четверти, и cos a<0, если a является углом II или III четверти.
В I и IV четвертях х > 0, а во II и III четвертях х < 0. Поэтому cos a > 0, если а является углом I или IV четверти, и cos a<0, если a является углом II или III четверти.
Так как 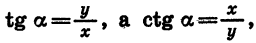 то знаки tg а и ctg а зависят от знаков х и у. В I и III четвертях хну имеют одинаковые знаки, а во II и IV — разные. Значит, tg a > 0 и ctg a > 0, если а является углом I или III четверти; tg a < 0 и ctg a < 0, если а является углом II или IV четверти.
то знаки tg а и ctg а зависят от знаков х и у. В I и III четвертях хну имеют одинаковые знаки, а во II и IV — разные. Значит, tg a > 0 и ctg a > 0, если а является углом I или III четверти; tg a < 0 и ctg a < 0, если а является углом II или IV четверти.
Знаки синуса, косинуса, тангенса и котангенса в каждой из четвертей показаны на рисунке 73.
Выясним теперь вопрос о четности и нечетности тригонометрических функций.
Пусть при повороте на угол а радиус OA переходит в радиус ОВ, а при повороте на угол — а в радиус ОС х (рис. 74). Соединив отрезком точки В и С, получим равнобедренный треугольник ВОС. Луч OA является биссектрисой угла ВОС. Значит, отрезок ОК является медианой и высотой треугольника ВОС. Отсюда следует, что точки В и С симметричны относительно оси абсцисс.
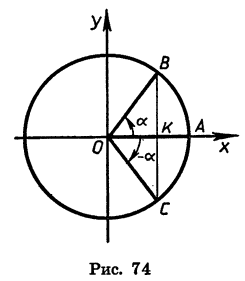
Пусть координаты точки В равны х и у, тогда координаты точки С равны х и -у. Пользуясь этим, найдем, что
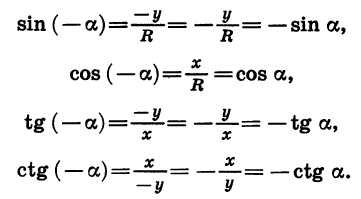
Мы получили формулы, выражающие зависимость между синусами, косинусами, тангенсами и котангенсами противоположных углов:
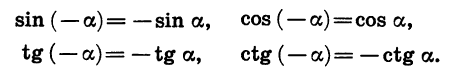
Например:
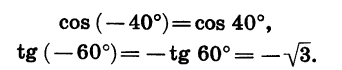
Итак, синус, тангенс и котангенс являются нечетными функциями, а косинус является четной функцией.
Рассмотрим еще одно свойство тригонометрических функций.
Если при повороте радиуса OA на угол а получен радиус ОВ (см. рис. 67), то тот же радиус получится и при повороте OA на угол, отличающийся от а на целое число оборотов. Отсюда следует, что при изменении угла на целое число оборотов значения синуса, косинуса, тангенса и котангенса не изменяются.
Например:
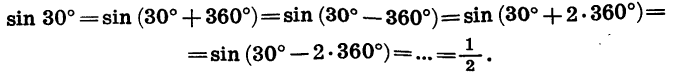
Рассмотренные свойства позволяют свести нахождение значений синуса, косинуса, тангенса и котангенса любого угла к нахождению их значений для неотрицательного угла, меньшего 360°.
Пример:
Найдем sin 765° и cos ( — 1170°). Имеем:
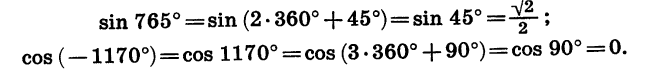
Радианная мера угла. Вычисление значении тригонометрических функции с помощью микрокалькулятора
Как известно, углы измеряются в градусах, минутах, секундах. Эти единицы измерения связаны между собой соотношениями
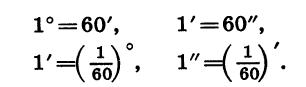
Кроме указанных, используется также единица измерения углов, называемая радианом.
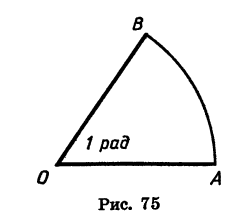
Углом в один радиан называют центральный угол, которому соответствует длина дуги, равная длине радиуса окружности.
Угол, равный 1 рад, изображен на рисунке 75.
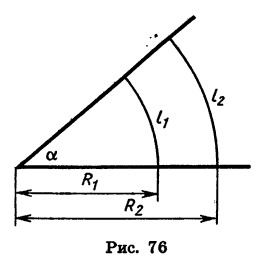
Радианная мера угла, т. е. величина угла, выраженная в радианах, не зависит О А от длины радиуса. Это следует из того, что фигуры, ограниченные углом и дугой окружности с центром в вершине этого угла, подобны между собой (рис. 76).
Установим связь между радиан-ным и градусным измерениями углов.
Углу, равному 180°, соответствует полуокружность, т. е. дуга, длина l которой равна 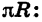
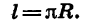
Чтобы найти радианную меру этого угла, надо длину дуги l разделить на длину радиуса R. Получим:
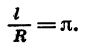
Следовательно, радианная мера угла в 180° равна 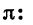
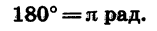
Отсюда получаем, что радианная мера угла в 1° равна 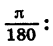
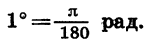
Приближенно 1° равен 0,017 рад.
Из равенства 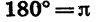 рад также следует, что градусная мера угла в 1 рад равна
рад также следует, что градусная мера угла в 1 рад равна 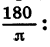
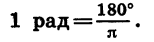
Приближенно 1 рад равен 57°.
Рассмотрим примеры перехода от радианной меры к градусной и от градусной меры к радианной.
Пример:
Выразим в градусах 4,5 рад.
Так как 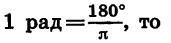
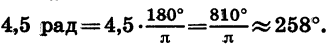
Пример:
Найдем радианную меру угла в 72°.
Так как 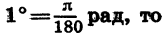
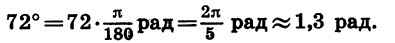
При записи радианной меры угла обозначение «рад» часто опускают. Например, вместо равенства 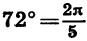 рад обычно пишут:
рад обычно пишут:
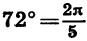
Выразим в радианной мере углы 30°, 45°, 60°, 90°, 270° и 360°. Получим:

Радианная мера угла часто используется в тригонометрических выражениях. Так, запись sirfl означает синус угла в 1 радиан, запись sin ( — 2,5) означает синус угла в —2,5 радиана, запись 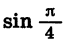 означает синус угла в
означает синус угла в 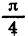 радиан. Вообще запись sin х, где х — произвольное действительное число, означает синус угла, равного х радианам.
радиан. Вообще запись sin х, где х — произвольное действительное число, означает синус угла, равного х радианам.
Значения тригонометрических функций для углов, выраженных как в градусах, так и в радианах, можно находить, используя микрокалькулятор. Так, с помощью микрокалькулятора «Электроника БЗ-З6» значения синуса, косинуса и тангенса вычисляют следующим образом. Переводят переключатель «ГРАД — РАД», находящийся в нижней части корпуса, в положение «ГРАД», если угол задан в градусах, или в положение «РАД», если угол задан в радианах. Вводят угол, нажимают клавишу  а затем клавишу, над которой написано название соответствующей функции.
а затем клавишу, над которой написано название соответствующей функции.
Пример:
Найдем с помощью микрокалькулятора значение выражения с точностью до 0,001:
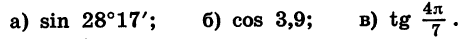
а) Установим переключатель в положение «ГРАД», затем выразим 28°17′ в градусах и нажмем «последовательно клавиши 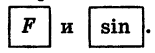 Так как
Так как 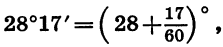 то программа вычислений выглядит так:
то программа вычислений выглядит так:

Получаем, что 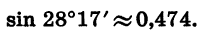
б) Устанавливаем переключатель в положение «РАД» и находим значение cos 3,9 по программе:
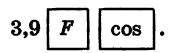
Получаем, что cos 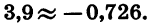
в) Переключатель устанавливаем в положение «РАД». При нахождении значения выражения 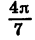 воспользуемся тем, что на панели микрокалькулятора «Электроника БЗ-З6» имеется специальная клавиша
воспользуемся тем, что на панели микрокалькулятора «Электроника БЗ-З6» имеется специальная клавиша 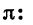 при нажатии которой высвечивается число 3,1415926 — приближенное значение числа
при нажатии которой высвечивается число 3,1415926 — приближенное значение числа 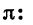 с точностью до
с точностью до 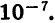 Вычисления проводим по программе:
Вычисления проводим по программе:

Получаем, что 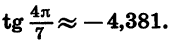
Отметим, что для вычисления котангенса угла надо сначала найти значение тангенса этого угла, а потом обратное число, нажав клавиши 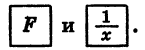
Основные тригонометрические формулы
Соотношения между тригонометрическими функциями одного и того же угла:
Рассмотрим, как связаны между собой синус и косинус одного и того же угла.
Пусть при повороте радиуса OA вокруг точки О на угол а получен радиус ОВ (рис. 77). По определению
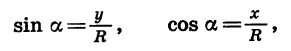
где х — абсцисса точки В, у — ее ордината, a R — длина радиуса OA. Отсюда

Так как точка В принадлежит окружности с центром в начале координат, радиус которой равен R, то ее координаты удовлетворяют уравнению
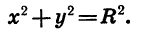
Подставив в это уравнение вместо х и у выражения R cos а и R sin а, получим:
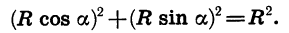
Разделив обе части последнего равенства на  найдем, что
найдем, что

Равенство (1) верно при любых значениях а. Выясним теперь, как связаны между собой тангенс, синус и косинус одного и того же угла.
По определению 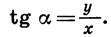 Так как y = R sin a, x = R cos a,
Так как y = R sin a, x = R cos a,
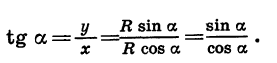
Таким образом,

Аналогично
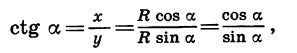
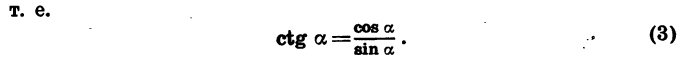
Равенство (2) верно при всех значениях а, при которых cos 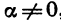 , а равенство (3) верно при всех значениях а, при которых sin
, а равенство (3) верно при всех значениях а, при которых sin 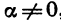
С помощью формул (1) — (3) можно получить другие формулы, выражающие соотношения между тригонометрическими функциями одного и того же угла.
Из равенств (2) и (3) получим:
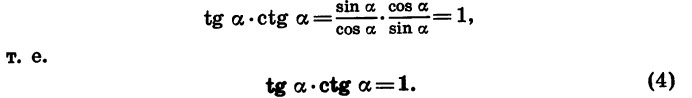
Равенство (4) показывает, как связаны между собой тангенс и котангенс угла а. Оно верно при всех значениях а, при которых tg а и ctg а имеют смысл.
Заметим, что формулу (4) можно получить и непосредственно из определения тангенса и котангенса.
Выведем теперь формулы, выражающие соотношения между тангенсом и косинусом, а также между котангенсом и синусом одного и того же угла.
Разделив обе части равенства (1) на 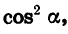 получим:
получим:
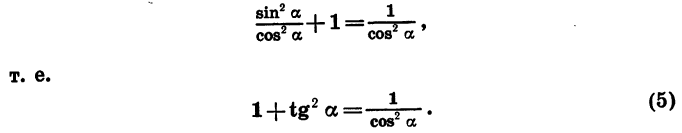
Если обе части равенства (1) разделить на 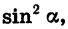 то будем иметь:
то будем иметь:
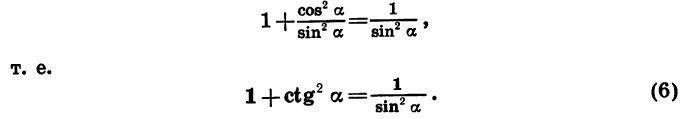
т. е.
Равенство (5) верно, когда cos 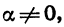 а равенство (6), когда sin
а равенство (6), когда sin 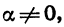
Равенства (1) — (6) являются тождествами. Их называют основными тригонометрическими тождествами. Рассмотрим примеры использования этих тождеств для нахождения значений тригонометрических функций по известному значению одной из них.
Пример:
Найдем cos a, tg а и ctg а, если известно, что sin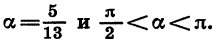
Найдем сначала cos а. Из формулы 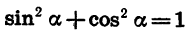 получаем, что
получаем, что 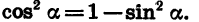
Так как а является углом II четверти, то его косинус отрицателен. Значит,
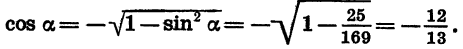
Зная синус и косинус угла а, можно найти его тангенс:
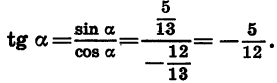
Для отыскания котангенса угла а удобно воспользоваться формулой tg a • ctg a = 1. Имеем:
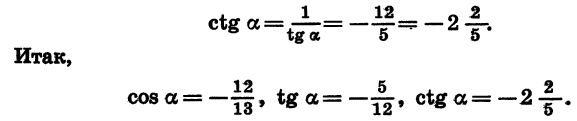
Пример:
Известно, что 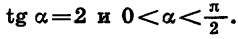 Найдем sin a, cos a и ctg a.
Найдем sin a, cos a и ctg a.
Воспользовавшись формулой 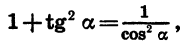 найдем cos a. Имеем:
найдем cos a. Имеем:
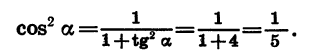
По условию угол a является углом I четверти, поэтому его косинус положителен. Значит,
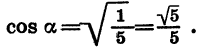
Зная cos а и tg а, можно найти sin а. Из формулы 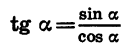 получим:
получим:
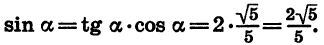
По известному tg а легко найти ctga:
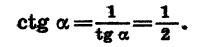
Итак,
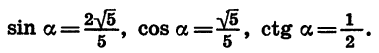
Применение основных тригонометрических формул к преобразованию выражении
Мы уже встречались с некоторыми простейшими преобразованиями тригонометрических выражений. Рассмотрим более сложные примеры.
Пример:
Упростим выражение 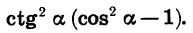
Воспользовавшись формулами 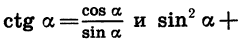
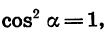 получим:
получим:
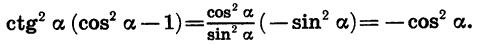
Пример:
Упростим выражение 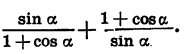
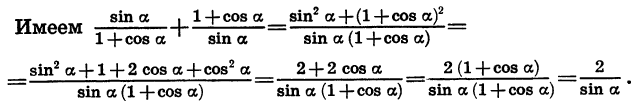
Пример:
Докажем тождество
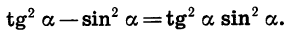
Преобразуем левую часть данного равенства:
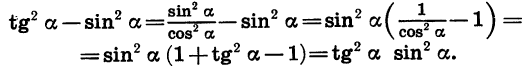
Мы получили выражение, стоящее в правой части равенства. Таким образом, тождество доказано.
Формулы приведения
Тригонометрические функции углов вида 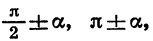
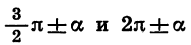 могут быть выражены через функции угла а с помощью формул, которые называют формулами приведения.
могут быть выражены через функции угла а с помощью формул, которые называют формулами приведения.
Выведем сначала формулы приведения для синуса и косинуса.
Докажем, что для любого а
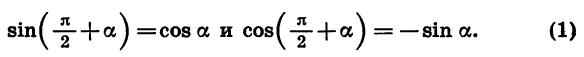
Повернем радиус OA, длина которого равна R, на угол а и на угол 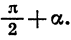 При этом радиус OA перейдет соответственно в радиусы ОВ1 и ОВ2 (рис. 78).
При этом радиус OA перейдет соответственно в радиусы ОВ1 и ОВ2 (рис. 78).
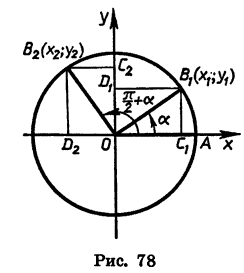
Опустим из точки В1 перпендикуляры 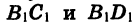 на оси координат. Получим прямоугольник
на оси координат. Получим прямоугольник 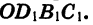
Повернем прямоугольник 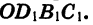 около точки О на угол
около точки О на угол 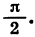 Тогда точка В1 перейдет в точку В2, точка С1 перейдет в точку С2 на оси у, точка D1 — в точку D2 на оси х, а прямоугольник
Тогда точка В1 перейдет в точку В2, точка С1 перейдет в точку С2 на оси у, точка D1 — в точку D2 на оси х, а прямоугольник 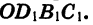 перейдет в равный ему прямоугольник
перейдет в равный ему прямоугольник 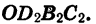
Отсюда следует, что ордината точки В2 равна абсциссе точки В1, а абсцисса точки В2 равна числу, противоположному ординате точки В1. Обозначим координаты точки B1 через 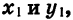 а координаты точки В2 через
а координаты точки В2 через 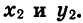 Тогда
Тогда
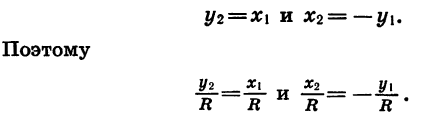
Значит,
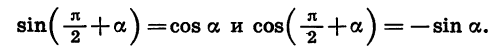
Из формул (1) следует, что
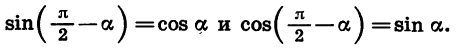
Действительно, представим разность 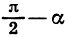 в виде суммы
в виде суммы 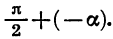 Тогда
Тогда
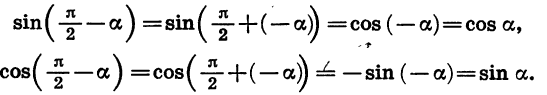
Формулы приведения для синуса и косинуса угла 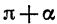 выглядят так:
выглядят так:
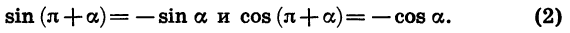
Для доказательства достаточно представить 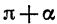 в виде
в виде 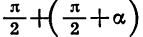 и дважды воспользоваться формулами (1). Например :
и дважды воспользоваться формулами (1). Например :
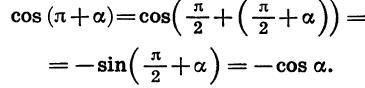
Заметим, что к формулам (2) легко прийти и из геометрических соображений (рис. 79). При повороте радиуса OA на угол а и на угол 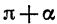 точка А перейдет соответственно в точки В1 и В2, которые симметричны относительно начала координат. Абсциссы, а также ординаты симметричных относительно
точка А перейдет соответственно в точки В1 и В2, которые симметричны относительно начала координат. Абсциссы, а также ординаты симметричных относительно
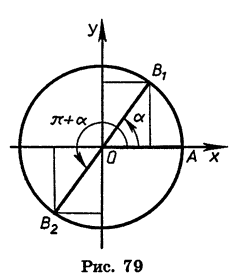
начала координат точек равны по модулю и противоположны по знаку. Отсюда следует, что 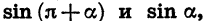 а также
а также 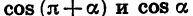 — противоположные числа.
— противоположные числа.
Из формул (2) следует, что
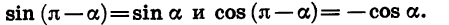
Для доказательства достаточно представить  в виде суммы
в виде суммы 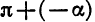 и применить формулы (2).
и применить формулы (2).
Формулы приведения для синуса и косинуса угла 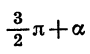 имеют вид:
имеют вид:
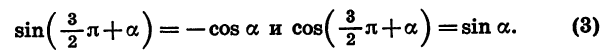
Чтобы доказать формулы (3), достаточно представить 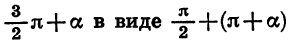 и применить последовательно формулы (1) и (2).
и применить последовательно формулы (1) и (2).
Из формул (3) нетрудно получить, что
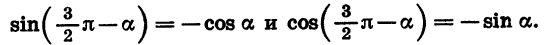
Наконец, формулы приведения для синуса и косинуса угла 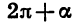 следуют из того, что при изменении угла на целое число оборотов значения синуса и косинуса не изменяются:
следуют из того, что при изменении угла на целое число оборотов значения синуса и косинуса не изменяются:
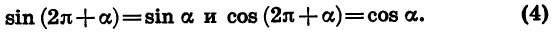
Справедливы также формулы
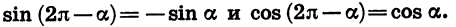
Например, для 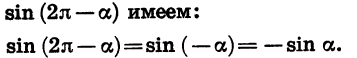
Формулы приведения для тангенса и котангенса можно получить с помощью формул приведения для синуса и косинуса. Например:
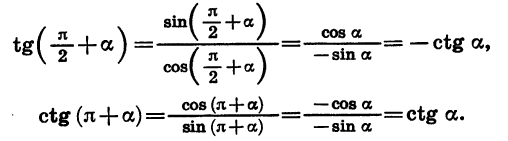
Все формулы приведения сведем в две таблицы, поместив в первой из них формулы для углов 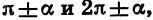 а во второй — для углов
а во второй — для углов 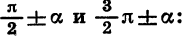
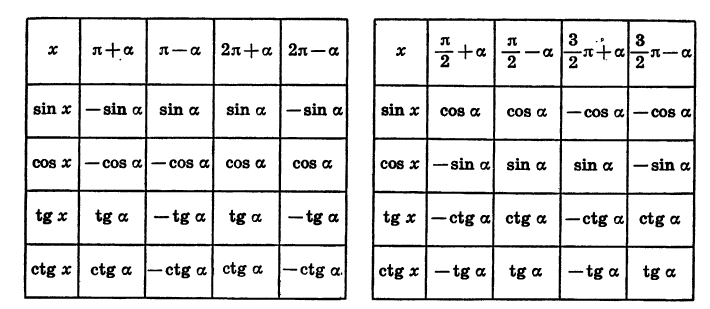
Цо таблицам легко проследить закономерности, имеющие место для формул приведения. Эти закономерности позволяют сформулировать правило, с помощью которого можно записать любую формулу приведения, не прибегая к таблице:
Функция в правой части равенства берется с тем же знаком, какой имеет исходная функция, если считать, что угол а является углом 1 четверти;
для углов 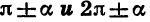 название исходной функции сохраняется; для углов
название исходной функции сохраняется; для углов 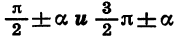 название исходной функции заменяется (синус на косинус, косинус на синус, тангенс на котангенс, котангенс на тангенс).
название исходной функции заменяется (синус на косинус, косинус на синус, тангенс на котангенс, котангенс на тангенс).
Пример:
Выразим 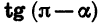 через тригонометрическую функцию угла а.
через тригонометрическую функцию угла а.
Если считать, что a — угол I четверти, то 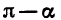 будет углом II четверти. Во II четверти тангенс отрицателен, значит, в правой части равенства следует поставить знак «минус». Для угла
будет углом II четверти. Во II четверти тангенс отрицателен, значит, в правой части равенства следует поставить знак «минус». Для угла 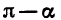 название исходной функции «тангенс» сохраняется. Поэтому
название исходной функции «тангенс» сохраняется. Поэтому
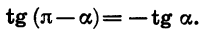
С помощью формул приведения нахождение значений тригонометрических функций любого угла можно свести к нахождению значений тригонометрических функций угла от 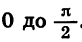 .
.
Пример:
Найдем значение 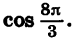
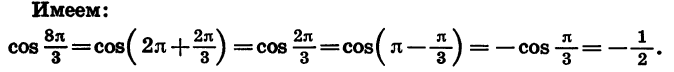
Пример:
Найдем значение sin (— 585°).
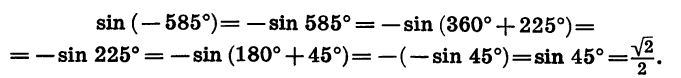
Формулы сложения и их следствия
Выведем формулы, выражающие тригонометрические функции суммы и разности двух углов через тригонометрические функции этих углов.
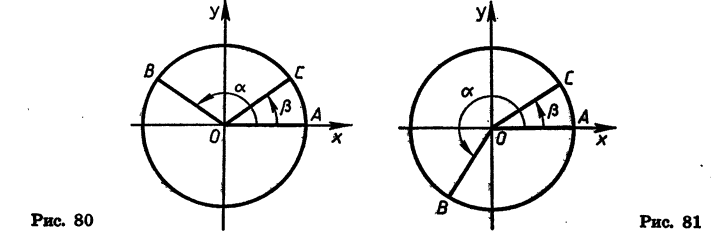
Повернем радиус OA, равный R, около точки О на угол а и на угол  (рис. 80). Получим радиусы ОВ и ОС.
(рис. 80). Получим радиусы ОВ и ОС.
Найдем скалярное произведение векторов 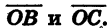 Пусть координаты точки В равны
Пусть координаты точки В равны 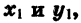 координаты точки С равны
координаты точки С равны 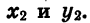 Эти же координаты имеют соответственно и векторы
Эти же координаты имеют соответственно и векторы 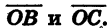 По определению скалярного произведения векторов:
По определению скалярного произведения векторов:
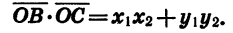
Выразим скалярное произведение 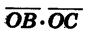 через тригонометрические функции углов а и
через тригонометрические функции углов а и  . Из определения косинуса и синуса следует, что
. Из определения косинуса и синуса следует, что
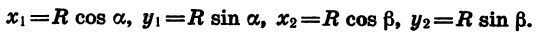
Подставив значения 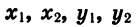 в правую часть равенства
в правую часть равенства 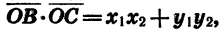 получим:
получим:
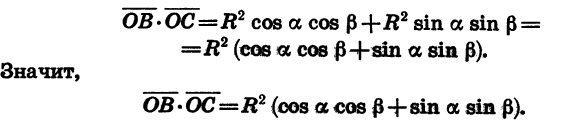
С другой стороны, по теореме о скалярном произведении векторов имеем:

Угол ВОС между векторами 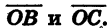 может быть равен а —
может быть равен а —  (см. рис. 80),
(см. рис. 80), 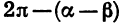 (рис. 81) либо может отличаться от этих значений на целое число оборотов. В любом из этих случаев cos
(рис. 81) либо может отличаться от этих значений на целое число оборотов. В любом из этих случаев cos 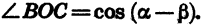 Поэтому
Поэтому
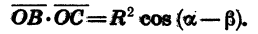
Так как 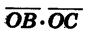 равно также
равно также 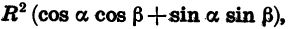 то
то
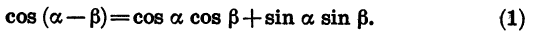
Формулу (1) называют формулой косинуса разности.
Косинус разности двух углов равен произведению косинусов этих углов плюс произведение синусов этих углов.
С помощью формулы (1) легко получить формулу косинуса суммы:
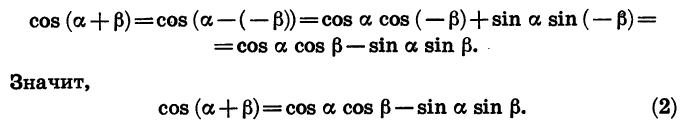
Косинус суммы двух углов равен произведению косинусов этих углов минус произведение синусов этих углов.
Выведем теперь формулы синуса суммы и синуса разности. Используя формулы приведения и формулу (1), получим:
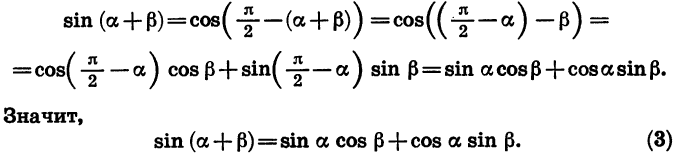
Синус суммы двух углов равен произведению синуса первого угла на косинус второго плюс произведение косинуса первого угла на синус второго.
Для синуса разности имеем:
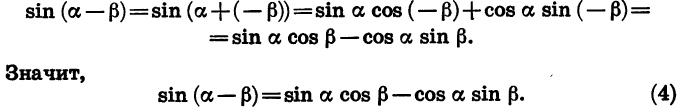
Синус разности двух углов равен произведению синуса первого угла на косинус второго минус произведение косинуса первого угла на синус второго.
Формулы (1) — (4) называют формулами сложения для синуса и косинуса.
Приведем примеры использования формул сложения.
Пример:
Вычислим cos 15° и sin 15°. Представим 15° в виде разности 45° — 30°. Тогда
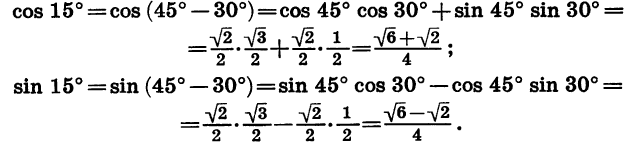
Пример:
Упростим выражение 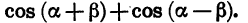 Воспользовавшись формулами косинуса суммы и косинуса разности, получим:
Воспользовавшись формулами косинуса суммы и косинуса разности, получим:
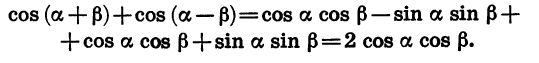
Используя формулы (1) — (4), можно вывести формулы сложения для тангенса и котангенса. Выведем, например, формулу тангенса суммы:
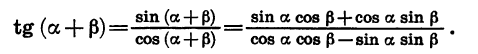
Разделим числитель и знаменатель полученной дроби на произведение cos a cos  , предполагая, что
, предполагая, что 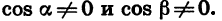 Получим:
Получим:
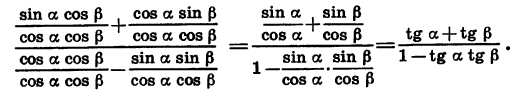
Значит,
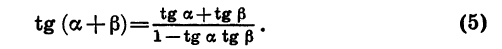
Аналогично можно доказать, что
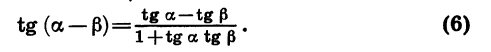
Формулы двойного угла
Формулы сложения позволяют выразить sin 2a, cos 2a и tg 2a через тригонометрические функции угла a. Положим в формулах
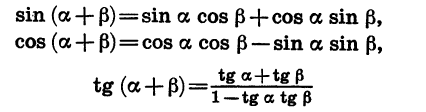
 равным a. Получим тождества:
равным a. Получим тождества:
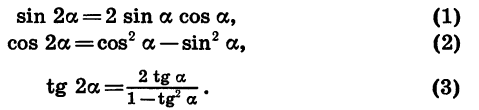
Эти тождества называют формулами двойного угла.
Приведем примеры применения формул двойного угла для нахождения значений тригонометрических функций и преобразования тригонометрических выражений.
Пример:
Найдем значение sin 2а, зная, что cosa = — 0,8 и a — угол III четверти.
Сначала вычислим sin а. Так как a — угол III четверти, то sin а < 0. Поэтому
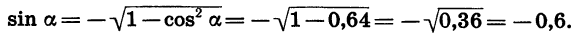
По формуле синуса двойного угла
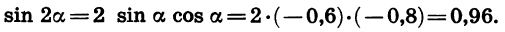
Пример:
Упростим выражение
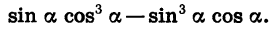
Вынесем за скобки sin a cos a и воспользуемся формулами двойного угла:
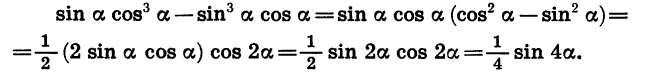
Из формулы (2) следует, что
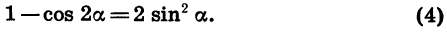
Действительно, выразив cos 2a через sin a, получим:
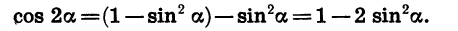
Отсюда 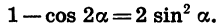
Аналогично, выразив cos 2a через cos a, получим:
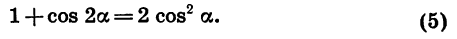
Формулы (4) и (5) используются в вычислениях и преобразованиях.
Пример:
Упростим выражение 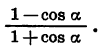
Применим формулы (4) и (5) к выражениям 1 — cos а и 1 + cos а, представив а в виде произведения 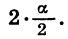 Получим:
Получим:
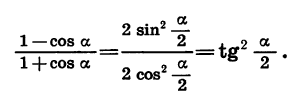
Формулы суммы и разности тригонометрических функции
Сумму и разность синусов или косинусов можно представить в виде произведения тригонометрических функций. Формулы, на которых основано такое преобразование, могут быть получены из формул сложения.
Чтобы представить в виде произведения сумму sin a + sin  , положим
, положим 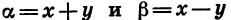 и воспользуемся формулами синуса суммы и синуса разности. Получим:
и воспользуемся формулами синуса суммы и синуса разности. Получим:
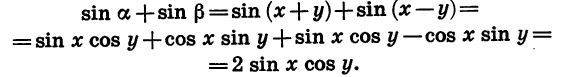
Из равенств a = x + y и  = x — y находим, что
= x — y находим, что 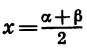 и
и 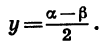 Поэтому
Поэтому
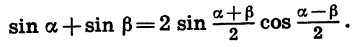
Мы получили формулу суммы синусов двух углов.
Сумма синусов двух углов равна удвоенному произведению синуса полусуммы этих углов на косинус их полуразности.
Аналогично можно вывести формулы разности синусов, суммы и разности косинусов.
Формула разности синусов:
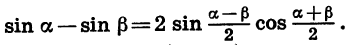
Разность синусов двух углов равна удвоенному произведению синуса полуразности этих углов на косинус их полусуммы.
Формула суммы косинусов:
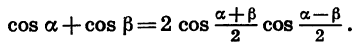
Сумма косинусов двух углов равна удвоенному произведению косинуса полусуммы, этих углов на косинус их полуразности.
Формула разности косинусов:
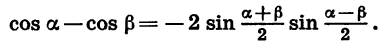
Разность косинусов двух углов равна взятому со знаком *минус» удвоенному произведению синуса полусуммы этих углов на синус их полуразности.
Учитывая, что 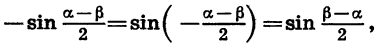 формулу разности косинусов можно записать в другом виде:
формулу разности косинусов можно записать в другом виде:
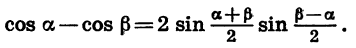
Приведем примеры применения полученных формул.
Пример:
Упростим сумму sin 10° + sin 50°.
Воспользовавшись формулой суммы синусов, получим:
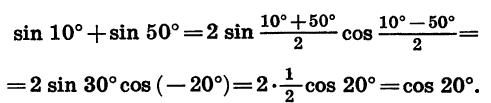
Пример:
Представим в виде произведения разность 
Воспользовавшись формулой приведения, представим данное выражение в виде разности косинусов и преобразуем ее в произведение. Тогда
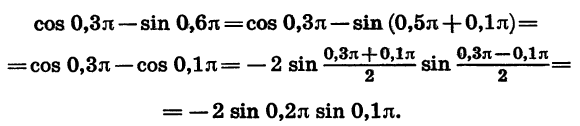
Пример:
Представим в виде произведения выражение 1 — sin а.
Так как 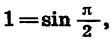 то данное выражение можно представить в виде разности синусов. Поэтому
то данное выражение можно представить в виде разности синусов. Поэтому
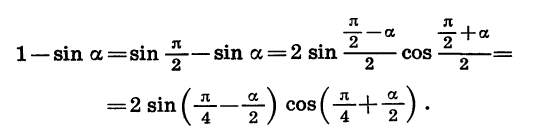
Эту задачу можно решить иначе:
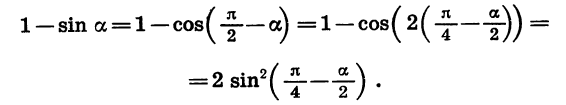
С помощью формул приведения первое из полученных выражений можно преобразовать во второе и наоборот.
Вычисление значений тригонометрических выражений
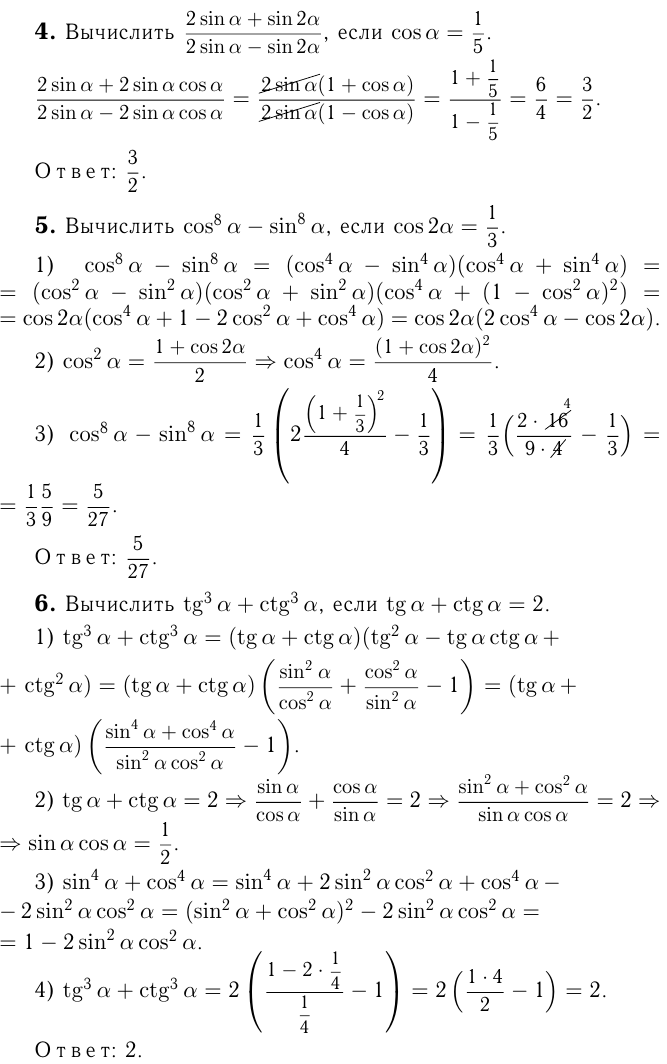






Возможно вам будут полезны эти страницы:
| Тригонометрия: определение и пример |
| Основные тригонометрические формулы |
| Что такое уравнение и как его решать |
| Квадратные уравнения задачи с решением |
Решение заданий и задач по предметам:
Дополнительные лекции по высшей математике:
- Тождественные преобразования алгебраических выражений
- Функции и графики
- Преобразования графиков функций
- Квадратная функция и её графики
- Алгебраические неравенства
- Неравенства
- Неравенства с переменными
- Прогрессии в математике
- Арифметическая прогрессия
- Геометрическая прогрессия
- Показатели в математике
- Логарифмы в математике
- Исследование уравнений
- Уравнения высших степеней
- Уравнения высших степеней с одним неизвестным
- Комплексные числа
- Непрерывная дробь (цепная дробь)
- Алгебраические уравнения
- Неопределенные уравнения
- Соединения
- Бином Ньютона
- Число е
- Непрерывные дроби
- Функция
- Исследование функций
- Предел
- Интеграл
- Двойной интеграл
- Тройной интеграл
- Интегрирование
- Неопределённый интеграл
- Определенный интеграл
- Криволинейные интегралы
- Поверхностные интегралы
- Несобственные интегралы
- Кратные интегралы
- Интегралы, зависящие от параметра
- Квадратный трехчлен
- Производная
- Применение производной к исследованию функций
- Приложения производной
- Дифференциал функции
- Дифференцирование в математике
- Формулы и правила дифференцирования
- Дифференциальное исчисление
- Дифференциальные уравнения
- Дифференциальные уравнения первого порядка
- Дифференциальные уравнения высших порядков
- Дифференциальные уравнения в частных производных
- Тригонометрические функции
- Тригонометрические уравнения и неравенства
- Показательная функция
- Показательные уравнения
- Обобщенная степень
- Взаимно обратные функции
- Логарифмическая функция
- Уравнения и неравенства
- Положительные и отрицательные числа
- Алгебраические выражения
- Иррациональные алгебраические выражения
- Преобразование алгебраических выражений
- Преобразование дробных алгебраических выражений
- Разложение многочленов на множители
- Многочлены от одного переменного
- Алгебраические дроби
- Пропорции
- Уравнения
- Системы уравнений
- Системы уравнений высших степеней
- Системы алгебраических уравнений
- Системы линейных уравнений
- Системы дифференциальных уравнений
- Арифметический квадратный корень
- Квадратные и кубические корни
- Извлечение квадратного корня
- Рациональные числа
- Иррациональные числа
- Арифметический корень
- Квадратные уравнения
- Иррациональные уравнения
- Последовательность
- Ряды сходящиеся и расходящиеся
- Тригонометрические функции произвольного угла
- Тригонометрические формулы
- Обратные тригонометрические функции
- Теорема Безу
- Математическая индукция
- Показатель степени
- Показательные функции и логарифмы
- Множество
- Множество действительных чисел
- Числовые множества
- Преобразование рациональных выражений
- Преобразование иррациональных выражений
- Геометрия
- Действительные числа
- Степени и корни
- Степень с рациональным показателем
- Тригонометрические функции угла
- Тригонометрические функции числового аргумента
- Преобразование тригонометрических выражений
- Комбинаторика
- Вычислительная математика
- Прямая линия на плоскости и ее уравнения
- Прямая и плоскость
- Линии и уравнения
- Прямая линия
- Уравнения прямой и плоскости в пространстве
- Кривые второго порядка
- Кривые и поверхности второго порядка
- Числовые ряды
- Степенные ряды
- Ряды Фурье
- Преобразование Фурье
- Функциональные ряды
- Функции многих переменных
- Метод координат
- Гармонический анализ
- Вещественные числа
- Предел последовательности
- Аналитическая геометрия
- Аналитическая геометрия на плоскости
- Аналитическая геометрия в пространстве
- Функции одной переменной
- Высшая алгебра
- Векторная алгебра
- Векторный анализ
- Векторы
- Скалярное произведение векторов
- Векторное произведение векторов
- Смешанное произведение векторов
- Операции над векторами
- Непрерывность функций
- Предел и непрерывность функций нескольких переменных
- Предел и непрерывность функции одной переменной
- Производные и дифференциалы функции одной переменной
- Частные производные и дифференцируемость функций нескольких переменных
- Дифференциальное исчисление функции одной переменной
- Матрицы
- Линейные и евклидовы пространства
- Линейные отображения
- Дифференциальные теоремы о среднем
- Теория устойчивости дифференциальных уравнений
- Функции комплексного переменного
- Преобразование Лапласа
- Теории поля
- Операционное исчисление
- Системы координат
- Рациональная функция
- Интегральное исчисление
- Интегральное исчисление функций одной переменной
- Дифференциальное исчисление функций нескольких переменных
- Отношение в математике
- Математическая логика
- Графы в математике
- Линейные пространства
- Первообразная и неопределенный интеграл
- Линейная функция
- Выпуклые множества точек
- Система координат
