Оглавление:
Совокупность двух алгебраических выражений, соединенных между собой знаком > (знак «больше») или знаком < (знак «меньше»), называют неравенством.
Примеры неравенств:
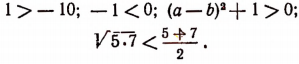
Два неравенства А > В и C>D называются неравенствами одинакового смысла. Таковы же и неравенства
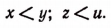
Два неравенства А >В и С<D называются неравенствами противоположного смысла.
Иногда приходится пользоваться знаком  (читается: «больше или равно») или знаком
(читается: «больше или равно») или знаком  (читается: «меньше или равно»). Например,
(читается: «меньше или равно»). Например,
 (равенство имеет место лишь при а = 0),
(равенство имеет место лишь при а = 0),
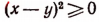 (равенство имеет место лишь при х = у).
(равенство имеет место лишь при х = у).
Если  (равенство имеет место лишь при
(равенство имеет место лишь при 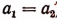 ).
).
Определение. Действительное число А называется большим действительного числа В, если разность А—В положительна.
Если же разность А — В отрицательна, то А меньше В.
Теорема:
Если обе части неравенства умножить или разделить на положительное число, то получится неравенство того же смысла.
Пусть А > В и m > 0. Тогда

Но по условиям теоремы А — B>0 и m > 0. Следовательно, Am—Вm > 0. Из последнего неравенства по определению следует, что Am > Вm, что и требовалось доказать.
Теорема:
Если обе части неравенства умножить или разделить на отрицательное число, то получится неравенство противоположного смысла.
Пусть A > B и m < 0. Тогда
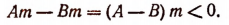
Следовательно,
Am > Вm.
Примем к сведению следующие положения, не останавливаясь на их доказательствах:
- Если A >B, то В<А.
- Если A > B и B > С, то A > С (транзитивность неравенств).
- Если A >B и Q—произвольное число, то A + Q > B + Q.
- Если A > В и С > D, то A + C > B + D.
- Если А>В и C<D, то A—C > B — D.
- Если A>B и C>D, то неизвестно, что больше А—С или B — D. Возможен и тот и другой случай.
- Если А>В и C>D и при этом числа А и D положительные, то АС>BD.
- Если А > В и если А и В — положительные числа, то
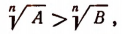 где n — натуральное число и где
где n — натуральное число и где 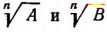 — арифметические значения корней.
— арифметические значения корней. - Неравенство
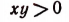
справедливо лишь тогда, когда хну либо одновременно положительны, либо одновременно отрицательны.
То же следует сказать и относительно неравенства
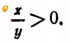
Доказательство неравенств
1. Доказать неравенство
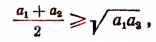
где 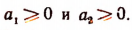
Чтобы доказать, что 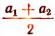 больше или равно
больше или равно 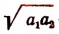 . Достаточно убедиться в том, что разность между
. Достаточно убедиться в том, что разность между 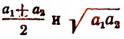 больше или равна нулю. Очевидно, что
больше или равна нулю. Очевидно, что
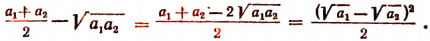
Но последнее выражение отрицательным быть не может. Следовательно,
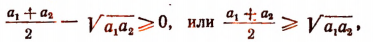
что и требовалось доказать. (Равенство имеет место лишь при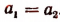 )
)
Число 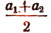 является средним арифметическим чисел
является средним арифметическим чисел 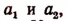 а число
а число 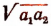 — их средним геометрическим.
— их средним геометрическим.
Из доказанного неравенства следует, что среднее арифметическое двух неотрицательных чисел не меньше их среднего геометрического.
2. Доказать неравенство
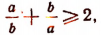
где а > 0 и b > 0.
Составим разность между левой и правой частями этого неравенства и убедимся в том, что она неотрицательна.
Очевидно, что 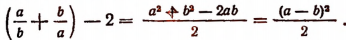
Последнее выражение отрицательным быть не может. Следовательно,
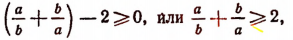
а это и требовалось доказать. (Равенство имеет место лишь при а = b.)
3. Доказать неравенство
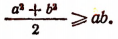
Очевидно, что
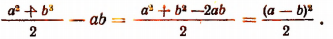
Отсюда
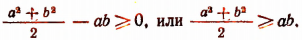
что и требовалось доказать. (Равенство имеет место лишь при а = b.)
4. Доказать неравенство
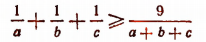
при условии, что a, b и с — положительные числа.
Докажем, что разность между левой и правой частями этого неравенства больше или равна нулю.
Очевидно, что
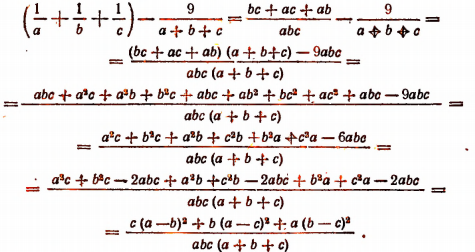
Но последнее выражение отрицательным быть не может. Следовательно,
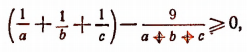
или
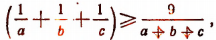
что и требовалось доказать. (Равенство имеет место лишь при условии, что a = b = с.)
5. Доказать неравенство
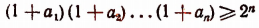
при условии, что числа 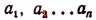 — положительны и что
— положительны и что
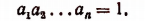
Доказательство:
Как уже было доказано, если х и у— числа неотрицательные, то
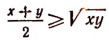
(см. пример 1).
Полагая 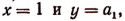 получим:
получим:
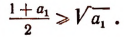
Аналогично
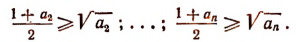
Перемножая левые и правые части этих неравенств, получим:
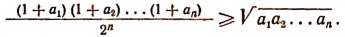
Но по условию 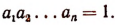 Поэтому
Поэтому 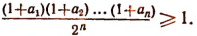
Отсюда
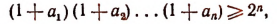
что и требовалось доказать.
6. Доказать, что неравенство
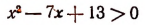
справедливо при всяком действительном значении х.
После выделения полного квадрата неравенство примет вид:
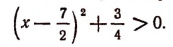
Но это неравенство справедливо при всяком действительном значении х. Следовательно, и первоначальное неравенство обладает этим свойством.
7. Доказать, что неравенство
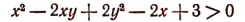
справедливо при любых действительных значениях х и у.
Преобразуем левую часть неравенства следующим образом:
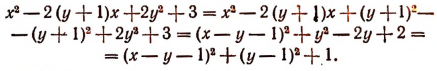
Теперь неравенство примет вид:
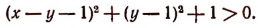
Левая часть этого неравенства, а следовательно, и левая часть первоначального неравенства положительна при любых действительных значениях х и у.
Неравенства с одним неизвестным
Примеры неравенств с одним неизвестным:
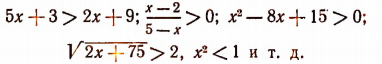
Решить неравенство с одним неизвестным — это значит найти все такие значения неизвестного, при которых это неравенство справедливо (или убедиться, что ни одного такого значения нет).
Решением неравенства называется всякое значение неизвестного, при котором неравенство справедливо.
Существуют неравенства, не имеющие ни одного решения.
Например, таковы неравенства:

Два неравенства называются равносильными, если любое решение одного из них является решением другого, и наоборот.
Аналогично двум основным теоремам о равносильности уравнений имеют место и теоремы о равносильности неравенств.
Теорема:
Если к обеим частям неравенства, содержащего неизвестное, прибавить одно и то же число или одно и то же выражение, то получим новое неравенство, равносильное данному. (Прибавляемое выражение должно быть определенным при тех же значениях неизвестного, при которых будут определенными одновременно левая и правая части данного неравенства.)
Теорема:
Если обе части неравенства умножить или разделить на положительное число, то получим неравенство того же смысла, равносильное данному.
Если же обе части неравенства умножить или разделить на отрицательное число, то получим неравенство противоположного смысла, равносильное данному.
Убедиться в справедливости этих свойств неравенств можно таким же путем, каким мы убеждались в верности теорем о равносильности уравнений.
Следствие из теоремы 1. Члены неравенства можно переносить с противоположным знаком из одной части неравенства в другую.
Следствие из теоремы 2. Неравенство с дробными коэффициентами можно преобразовывать в неравенство с целыми коэффициентами.
Неравенство можно сокращать на общий множитель всех его членов, не содержащий неизвестного. Если этот общий множитель положительный, то смысл неравенства сохранится, а если отрицательный, то изменится на противоположный.
Примечание. Нельзя умножать или делить члены неравенства на выражение, если неизвестно, каким числом, положительным или отрицательным, оно является.
Решение неравенств первой степени с одним неизвестным
Всякое неравенство первой степени с одним неизвестным можно привести к виду
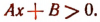
- Если А>0, то
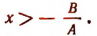
- Если А < 0, то
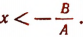
- Если А = 0 и В > 0, то неравенство справедливо при любом значении х.
- Если А = 0 и В < 0, то неравенство решения не имеет.
Пример:
Решить неравенство
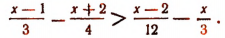
Умножив левую и правую части неравенства на 12, получим:
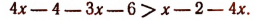
Перенесем члены, содержащие неизвестное, в левую часть, а известные в правую:
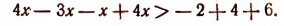
Отсюда
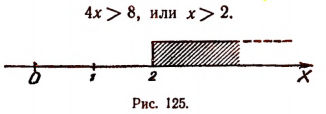
Все действия, выполненные нами (умножение на 12, перенесение членов из одной части неравенства в другую с противоположным знаком), как мы видели, оставляют неравенства равносильными. Следовательно, данное неравенство справедливо при тех же значениях х, при которых справедливо неравенство х > 2.
Следовательно, данное неравенство удовлетворяется при всех значениях х, больше двух. На числовой оси эти значения изображаются всеми точками, лежащими справа от точки х=2 (рис. 125).
Решение систем неравенств первой степени
Системой неравенств называется совокупность неравенств, в которых под одной и той же буквой, обозначающей неизвестное, подразумевается одна и та же величина.
Чтобы указать, что неравенства, например 2х—3>0 и 5—4х>0, рассматриваются как система неравенств, записывают так:
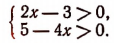
Решить систему неравенств с одним неизвестным— значит найти все те значения неизвестного, при которых оба неравенства системы становятся одновременно справедливыми, либо убедиться, что ни одного такого значения неизвестного не существует.
Всякое значение неизвестного, удовлетворяющее одновременно всем неравенствам системы, называется решением этой системы.
Примеры:
1. Решить систему:
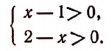
Решив первое неравенство, получим:
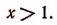
Решив второе неравенство, получим:
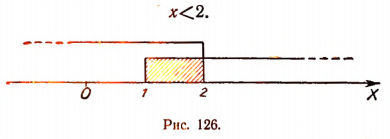
Следовательно, данная система удовлетворяется только при тех значениях х, которые заключены между 1 и 2 (рис. 126), т. е. 1<х<2.
2. Решить систему:
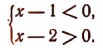
Решив первое неравенство, получим:
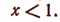
Решив второе, получим:
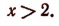
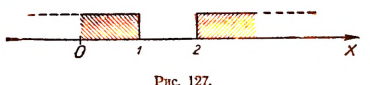
Следовательно, система не имеет ни одного решения, так как нет такого числа, которое было бы одновременно больше 2 и меньше 1 (рис. 127).
3. Решить систему:
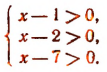
Эта система приводится к следующей:
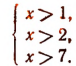
Следовательно, данная система удовлетворяется лишь при всех значениях х, больших 7.
4. Решить систему:
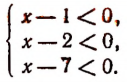
Эта система приводится к следующей:
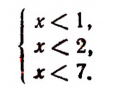
Следовательно, данная система удовлетворяется лишь при всех значениях х, меньших 1.
5. Решить систему:
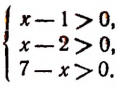
Эта система приводится к виду:
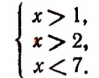
Следовательно, данная система удовлетворяется лишь при всех значениях х, заключенных между числами 2 и 7, т. е. 2 < х< 7.
Иногда решение одного неравенства сводится к решению систем неравенств. Например, решениями неравенства
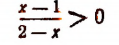
будут только решения следующих двух систем:

Решениями неравенства
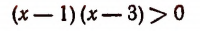
будут только решения следующих двух систем:

Пример:
Решить неравенство
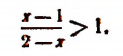
Здесь нежелательно умножать обе части неравенства на выражение  , так как мы не знаем, каким числом, положительным или отрицательным, оно является.
, так как мы не знаем, каким числом, положительным или отрицательным, оно является.
Решение этого неравенства надо начинать с переноса всех членов этого неравенства в левую часть. Перенеся все члены неравенства в левую часть, получим:
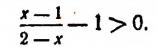
Преобразуя левую часть этого неравенства, получим:
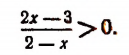
Решениями последнего неравенства будут только решения следующих двух систем:

Первая система удовлетворяется при всех значениях х, заключенных между 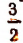 и 2.
и 2.
Вторая система не имеет ни одного решения. Следовательно, и первоначальное неравенство удовлетворяется лишь при значениях х, заключенных между 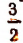 и 2, т. е.
и 2, т. е. 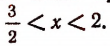
Пример:
Решить неравенство
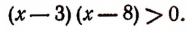
Решениями этого неравенства будут только решения следующих двух систем:

Следовательно, первоначальное неравенство будет удовлетворяться как при всех значениях х, больших 8, так и при всех значениях х, меньших 3.
Решение неравенств второй степени
Всякое неравенство второй степени может быть приведено к виду:
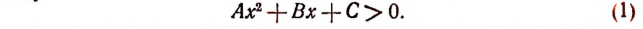
В самом деле, если имеем неравенство вида 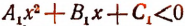 , то, умножив обе части этого неравенства на — 1 и изменив знак неравенства на противоположный, получим неравенство
, то, умножив обе части этого неравенства на — 1 и изменив знак неравенства на противоположный, получим неравенство 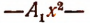
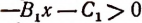 вида (1). Поэтому неравенство (1) называется общим видом неравенства второй степени.
вида (1). Поэтому неравенство (1) называется общим видом неравенства второй степени.
1. Решения неравенства 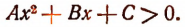
1.Случай, когда 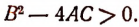
(Выражение 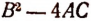 называется дискриминантом трехчлена
называется дискриминантом трехчлена 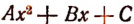 .)
.)
В этом случае данное неравенство можно записать в следующем виде (см. стр. 298):
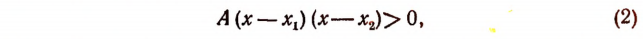
где 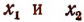 —действительные и различные корни трехчлена
—действительные и различные корни трехчлена
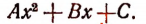
Будем считать, что буквой 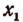 обозначен больший корень, а буквой
обозначен больший корень, а буквой 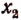 — меньший.
— меньший.
Пусть А > 0. Тогда в решение неравенства (2), а следовательно, и (1) войдут только решения следующих двух систем:

Отсюда легко заключить, что решением данного неравенства будет совокупность всех чисел, больших 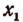 , а также совокупность всех чисел, меньших
, а также совокупность всех чисел, меньших 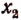 .
.
Пусть теперь А < 0. Тогда дело сведется к решению следующих двух систем:

Первая из этих двух систем не имеет ни одного решения. Вторая же система удовлетворяется при всех значениях х, заключенных между 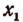 и
и 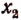 .
.
Следовательно, и данное неравенство 2-й степени будет удовлетворяться лишь значениями х, заключенными между корнями 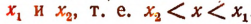
2. Случай, когда 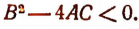
Пользуясь выделением полного квадрата, запишем данное неравенство в виде:
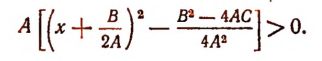
Пусть А > 0. Тогда неравенство удовлетворяется при всяком значении х, так как 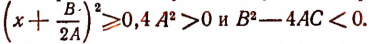
Пусть А < 0. Тогда неравенство не имеет ни одного решения.
3. Случай, когда В
Опять запишем данное неравенство в виде:
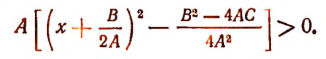
Пусть А > 0. Тогда данное неравенство удовлетворяется при всяком значении х, кроме 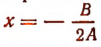 .
.
Пусть А < 0. Тогда данное неравенство не имеет ни одного решения.
Если А > 0 и если неравенство 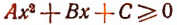 справедливо при всяком значении х, то дискриминант многочлена
справедливо при всяком значении х, то дискриминант многочлена 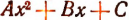 , т. е. выражение
, т. е. выражение 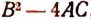 , не может оказаться положительным. Это следует из того, что при А > 0 и
, не может оказаться положительным. Это следует из того, что при А > 0 и 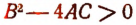 неравенство
неравенство
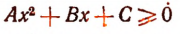
удовлетворялось бы не любыми значениями х.
2. Выводы, относящиеся к решению неравенства
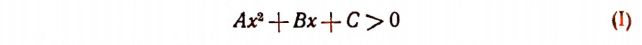
1. Если 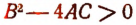 и А > 0, то неравенство (I) будет удовлетворяться как значениями х, большими большего корня, так и значениями х, меньшими меньшего корня многочлена
и А > 0, то неравенство (I) будет удовлетворяться как значениями х, большими большего корня, так и значениями х, меньшими меньшего корня многочлена
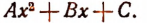
2. Если 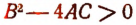 и А < 0, то неравенство (I) будет удовлетворяться всеми значениями х, заключенными между корнями
и А < 0, то неравенство (I) будет удовлетворяться всеми значениями х, заключенными между корнями 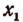 и
и 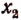 , многочлена
, многочлена 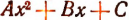 .
.
3. Если 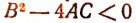 и А > 0, то неравенство (1) будет удовлетворяться при любом действительном значении х.
и А > 0, то неравенство (1) будет удовлетворяться при любом действительном значении х.
4. Если 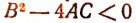 и А < 0, то неравенство (I) не будет удовлетворяться ни при каком значении х.
и А < 0, то неравенство (I) не будет удовлетворяться ни при каком значении х.
5. Если 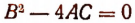 и А>0, то неравенство (I) будет удовлетворяться при всяком значении х, за исключением значения
и А>0, то неравенство (I) будет удовлетворяться при всяком значении х, за исключением значения
6. Если 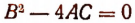 и А < 0, то неравенство (I) не может удовлетворяться ни при каком значении х.
и А < 0, то неравенство (I) не может удовлетворяться ни при каком значении х.
Примечание. Запоминать эти выводы нет смысла, так как пользоваться ими приходится очень редко. Лучше всего закрепить в своей памяти не эти 6 выводов, а тот способ, с помощью которого они получаются. Прежде всего надо закрепить в своей памяти то, что при 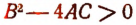 надо прибегать к разложению многочлена
надо прибегать к разложению многочлена 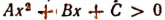 на линейные множители, а в случае
на линейные множители, а в случае 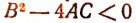 выделять полный квадрат.
выделять полный квадрат.
3. Геометрическая интерпретация решений неравенства 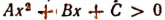 .
.
Мы знаем, что графиком функции 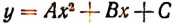 является парабола с осью, параллельной оси
является парабола с осью, параллельной оси 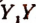 . Ордината вершины этой параболы равна
. Ордината вершины этой параболы равна 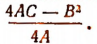
Парабола простирается неограниченно вверх, если А > 0, и вниз, если А < 0 (см. стр. 341).
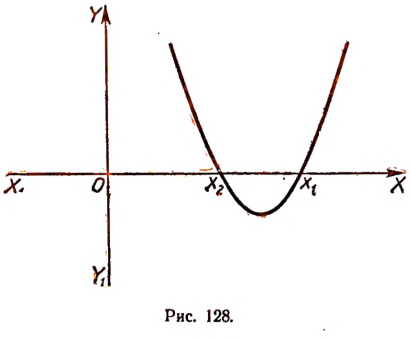
1. Пусть 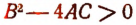 и А >0, тогда
и А >0, тогда 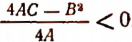 . В этом случае вершина параболы будет лежать в нижней полуплоскости и сама парабола будет простираться вверх (рис. 128) (
. В этом случае вершина параболы будет лежать в нижней полуплоскости и сама парабола будет простираться вверх (рис. 128) (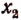 и
и 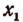 — корни многочлена
— корни многочлена 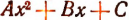 ;
; 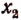 — меньший корень, а
— меньший корень, а 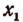 — больший).
— больший).
Из рисунка 128 мы видим, что значения трехчлена 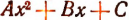 , т. е. ординаты точек параболы, положительны как при
, т. е. ординаты точек параболы, положительны как при 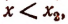 так и при
так и при 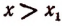 .
.
2. Пусть 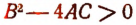 и А <0. В этом случае вершина параболы будет лежать в верхней полуплоскости и сама парабола будет простираться вниз (рис. 129).
и А <0. В этом случае вершина параболы будет лежать в верхней полуплоскости и сама парабола будет простираться вниз (рис. 129).
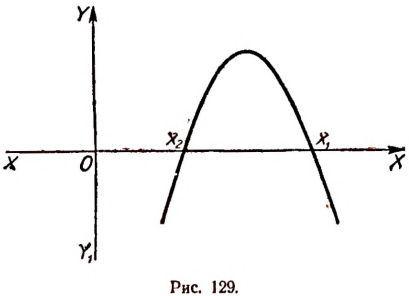
Из рисунка 129 мы видим, что значения трехчлена 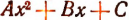 положительны при
положительны при 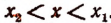 .
.
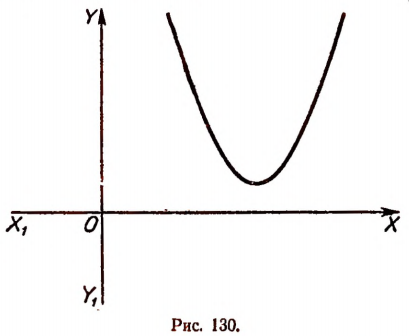
3. Пусть 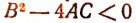 и А > 0. В этом случае вершина параболы будет лежать в верхней полуплоскости и сама парабола будет простираться вверх (рис. 130).
и А > 0. В этом случае вершина параболы будет лежать в верхней полуплоскости и сама парабола будет простираться вверх (рис. 130).
На рисунке 130 мы видим, что значения трехчлена 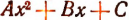 положительны при всех значениях х.
положительны при всех значениях х.
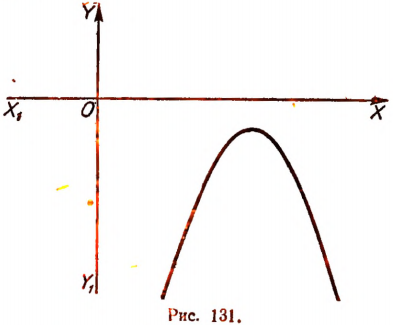
4. Пусть 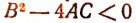 и А < 0. В этом случае вершина параболы будет лежать в нижней полуплоскости и сама парабола будет простираться вниз (рис. 131).
и А < 0. В этом случае вершина параболы будет лежать в нижней полуплоскости и сама парабола будет простираться вниз (рис. 131).
На рисунке 131 мы видим, что значения трехчлена 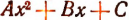 не могут быть положительными ни при каком значении х.
не могут быть положительными ни при каком значении х.
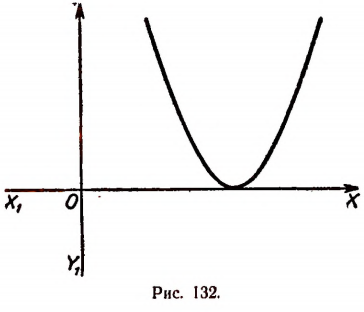
5. Пусть 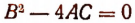 и А > 0. В этом случае вершина параболы будет лежать на оси
и А > 0. В этом случае вершина параболы будет лежать на оси  и парабола будет простираться вверх (рис. 132).
и парабола будет простираться вверх (рис. 132).
На рисунке 132 мы видим, что значения трехчлена 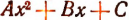 будут положительными при всех значениях х, за исключением
будут положительными при всех значениях х, за исключением
единственного значения 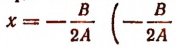 есть абсцисса вершины параболы).
есть абсцисса вершины параболы).
6. Пусть 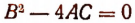 и А < 0. В этом случае вершина параболы будет лежать на оси
и А < 0. В этом случае вершина параболы будет лежать на оси  и парабола будет простираться вниз (рис. 133).
и парабола будет простираться вниз (рис. 133).
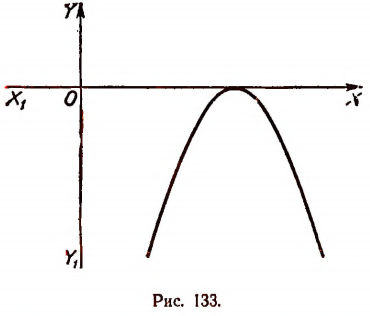
На рисунке 133 мы видим, что значения трехчлена 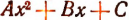 не могут быть положительными ни при каком значении х.
не могут быть положительными ни при каком значении х.
Примеры решения неравенств
1. Решить неравенство
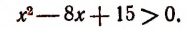
Здесь
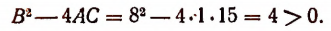
Поэтому решение данного неравенства сведется к решению неравенства
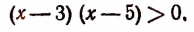
Отсюда
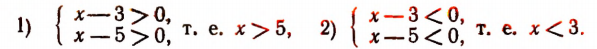
Значит, данному неравенству будут удовлетворять как все значения х, меньшие трех, так и все значения, большие пяти, и никакие другие.
2. Решить неравенство
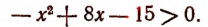
Умножив обе части неравенства на —1, получим:
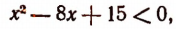
или
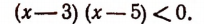
Отсюда
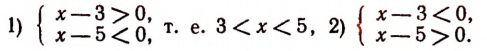
Последняя, т. е. вторая, система неравенств решений не имеет.
Значит, неравенству 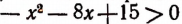 удовлетворяют только значения х, заключенные между числами 3 и 5.
удовлетворяют только значения х, заключенные между числами 3 и 5.
Замечания. а) Из неравенства 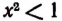 следует, что
следует, что 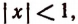 т. е. что — 1 <х< 1.
т. е. что — 1 <х< 1.
б) Из неравенства 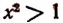 имеем, что
имеем, что 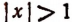 , т. е. что либо х < — 1, либо же х > 1.
, т. е. что либо х < — 1, либо же х > 1.
3. Решить неравенство 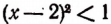 .
.
Из данного неравенства получается, что 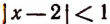 , т. е. что
, т. е. что 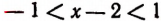 . Из неравенства
. Из неравенства 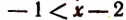 следует, что х > 1, а из неравенства х — 2< 1 получается, что х < 3.
следует, что х > 1, а из неравенства х — 2< 1 получается, что х < 3.
Итак, данное неравенство удовлетворяется лишь значениями х, лежащими между числами 1 и 3, т. е. принадлежащими промежутку (1; 3).
4. Решить неравенство
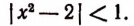
Из данного неравенства следует, что
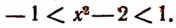
Сначала решим неравенство
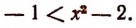
Из этого неравенства следует, что
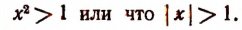
Теперь решим неравенство
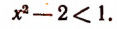
Из этого неравенства следует, что

Итак, неравенству
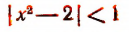
удовлетворяют такие и только такие значения х, которые определяются следующими двумя неравенствами:
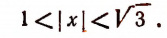
Последним же двум неравенствам удовлетворяют как все числа, заключенные между 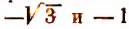 , так и все числа, заключенные между
, так и все числа, заключенные между 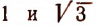 (см. рис. 134).
(см. рис. 134).

5. При каких значениях m неравенство
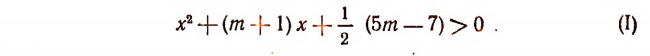
справедливо для любого действительного значения х?
Решим эту задачу двумя способами.
Способ 1. Неравенство
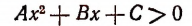
справедливо при любом значении х тогда и только тогда, когда
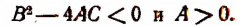
В неравенстве (1) А = 1 > 0. Поэтому остается потребовать выполнения неравенства
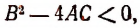
т. е. неравенства
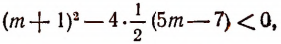
которое после преобразования принимает вид
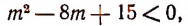
или
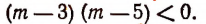
В решение последнего неравенства войдут только решения следующих двух систем:
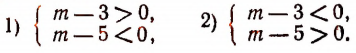
Вторая система не имеет ни одного решения, а первая удовлетворяется при всех значениях m, заключенных между 3 и 5.
Следовательно, первоначальное неравенство будет справедливым при любых значениях х лишь тогда, когда число т будет заключаться между 3 и 5, т. е. когда 3<m<5.
Способ 2. График функции
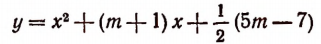
есть парабола, бесконечно простирающаяся вверх, так как коэффициент при 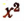 положительный.
положительный.
Для того чтобы ордината у была положительной при всяком значении х, необходимо и достаточно, чтобы вершина этой параболы лежала в верхней полуплоскости, т. е. необходимо и достаточно, чтобы ордината вершины параболы была положительной. Но ордината вершины параболы
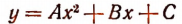
равна
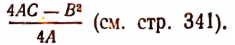
Поэтому имеем:
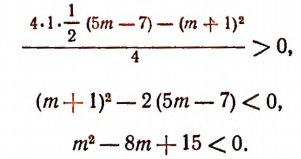
Дальше ход рассуждений тот же, что и в первом способе.
6. Доказать неравенство Буняковского — Коши:
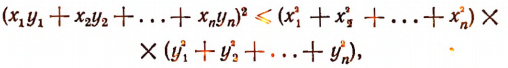
где 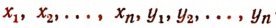 — любые действительные числа.
— любые действительные числа.
Доказательство:
Ясно, что
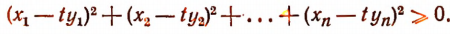
Отсюда
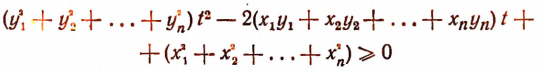
при всяком действительном значении t.
Следовательно, дискриминант левой части неравенства будет меньше или равен нулю, т. е.
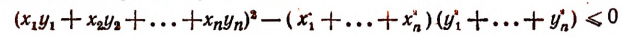
(см. замечание на стр. 389).
Отсюда
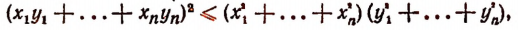
что и требовалось доказать.
Неравенства и их решение
Неравенства – выражения вида a > b , a < b , a ≤ b и a ≥ b , где a и b – числа или выражения с переменной.
Основные свойства неравенств
Пусть а и b — какие-нибудь вещественные числа. Если разность а — b положительна, то говорят, что а больше b:
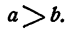
Если разность а — b отрицательна, то говорят, что а меньше b:

Точно так же, если а > b, то разность а — b положительна, если же а < b, то разность а — b отрицательна.
Для того чтобы высказать утверждение, что численное значение какого-нибудь алгебраического выражения больше или меньше численного значения другого алгебраического выражения, их соединяют знаком 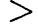 или
или 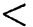 и, таким образом, составляют неравенство.
и, таким образом, составляют неравенство.
Из определения вытекает, что неравенство а > 0 означает, что а положительно, и неравенство а < 0 означает, что а отрицательно.
Если в каждом из двух или нескольких неравенств левая часть больше правой или в каждом из неравенств левая часть меньше правой, то такие неравенства называются неравенствами одинакового смысла. Например, неравенства а > b и c > d имеют одинаковый смысл.
Если же в одном неравенстве левая часть больше правой, а в другом левая часть меньше правой, то такие неравенства называются неравенствами противоположного смысла.
Теорема:
Если а > b , то b < а, и, наоборот, если b < а , то а > b.
Доказательство:
По условию разность а — b положительна. А тогда разность b — а отрицательна. Следовательно,

Обратное утверждение доказывается точно так же.
Теорема:
Если а > b , b > с, то а > с.
Доказательство:
Пусть

Сложив равенства (1) и (2) почленно, получим
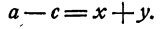
Так как х и у положительны, то х +у > 0 и потому а > с.
Другое доказательство. Рассмотрим разность
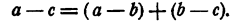
По условию каждая из разностей а — b и b— с положительна, значит, а — c > 0, т. е. а > с.
Теорема:
Если а > b, то при любом с
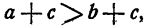
т. е. неравенство не нарушается*), если к каждой части его прибавить одно и то же число.
Доказательство:
Пусть а — b = х, тогда
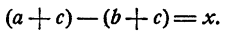
Так как, по условию, х > 0, то a + с > b + с.
Другое доказательство. Рассмотрим равенство
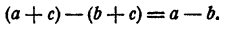
По условию а — b> 0, значит, а + с > b + c
Следствие:
Любое слагаемое можно перенести из одной части неравенства в другую, изменив при этом знак его на противоположный.
Доказательство:
Пусть
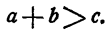
Прибавим к каждой части неравенства — b, получим
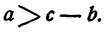
Слагаемое b перенесено из левой части в правую с противоположным знаком.
Теорема:
Если а > b и с > 0, то ас > bс, если а > b и с < 0, то ас < bс, если а > b и с = 0, то ас = be, т. е. неравенство не нарушается, если обе части его умножить на одно и то же положительное число;
неравенство превращается в неравенство противоположного смысла, если обе части его умножить на одно и то же отрицательное число;
неравенство превращается в равенство, если обе части его умножить на нуль
*) Выражение «неравенство не нарушается» означает, что неравенство преобразуется в другое неравенство одинакового с ним смысла.
Доказательство:
Пусть
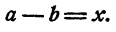
Тогда ас — bс = xс. По условию, x > 0.
Если c > 0 то произведение xс положительно и ас > bс.
Если c < 0, то произведение xс отрицательно и ас < bс.
Если с = 0, то произведение xс равно нулю и ас = be.
Теорема:
Если a > b и c > d, то a + с > b + d, т. е. при почленном сложении двух неравенств одного и того же смысла получается неравенство того же смысла.
Доказательство:
Пусть

Сложив равенства (3) и (4) почленно, получим
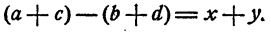
Так как х и у положительны, то x + y > 0 и а + с > b+d.
Теорема:
Если а, b, с, d положительны и a > b, c > d, то ac > bd, т. е. при почленном умножении двух неравенств, имеющих положительные члены и один и тот же смысл, получается неравенство того же смысла.
Доказательство:
Пусть
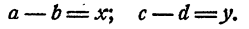
Тогда
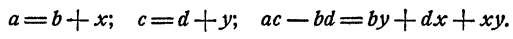
Так как х > 0; у > 0; b > 0 и d > 0, то правая часть последнего равенства положительна и ac > bd.
Теорема:
Если а > b > 0, то при любом натуральном n 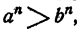 т. е. неравенство, имеющее положительные члены, не нарушается, если каждую часть его возвести в степень с одним и тем же натуральным показателем.
т. е. неравенство, имеющее положительные члены, не нарушается, если каждую часть его возвести в степень с одним и тем же натуральным показателем.
Доказательство:
При п = 1 утверждение справедливо по условию. Допустим, что утверждение справедливо при n = k, где fe-какое-нибудь Натуральное число, т. е. 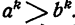 Умножим предыдущее неравенство почленно на неравенство а > b, получим
Умножим предыдущее неравенство почленно на неравенство а > b, получим
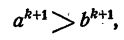
т. е. утверждение справедливо и при n = k + 1.
Замечание:
Если а и b отрицательны или имеют разные знаки, или одно из них равно нулю, то из а > b может не следовать 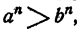 Например, -3 < -2, однако (-3)² > (-2)²; -3 < 2, однако (— 3)² > 2²; — 3 < 0, однако (— 3)² > 0.
Например, -3 < -2, однако (-3)² > (-2)²; -3 < 2, однако (— 3)² > 2²; — 3 < 0, однако (— 3)² > 0.
Теорема:
Если а > b, то при любом n 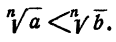
Доказательство:
Допустим, что
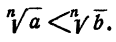
Тогда на основании теоремы 7 имеем а < b, что противоречит условию.
Очевидно, что нельзя предполагать и то, что
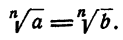
Неравенство а > b называется строгим неравенством, неравенство а ≥ b называется нестрогим неравенством.
Теоремы 1—8 доказаны для строгих неравенств. Нетрудно показать, что все они справедливы и для нестрогих неравенств. Так, например, теорему 1 можно сформулировать так:
Если а ≥ b, то b ≤ а и, наоборот, если b ≤ а, то a ≥ b.
Доказательство:
Выше было доказано, что утверждение справедливо для строгих неравенств. С другой стороны, известно, что аналогичное утверждение справедливо и для равенств, т. е. если a = b, то b = а и, наоборот, если b = а, то а = b. Утверждение для нестрогих неравенств является объединением двух аналогичных утверждений, из которых одно справедливо для строгих неравенств, а другое— для равенств.
Доказательство неравенств
При решении различных вопросов возникает потребность в выяснении, которое из двух данных чисел больше другого. Такие задачи называются задачами на выяснение знака неравенств. Например, выяснить, какие корни имеет уравнение
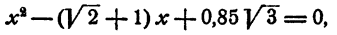
вещественные или мнимые? Для решений этого вопроса надо выяснить, что больше
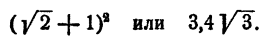
В некоторых задачах знак неравенства указан в условии задачи, и требуется доказать, что данное неравенство справедливо. Такие задачи называются задачами на доказательство неравенств. Например, доказать, что при любых положительных а и b
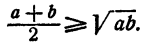
Между указанными двумя типами задач нет существенного различия, так как при установлении знака неравенства одновременно доказывается справедливость некоторого неравенства и наоборот.
Задачи на доказательство неравенств могут быть весьма разнообразны, а потому разнообразны и приемы их решения. Основные приемы доказательства неравенств поясняются следующими примерами.
Пример:
Какие корни имеет уравнение
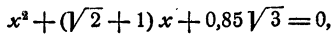
действительные или мнимые?
Решение:
Для ответа на этот вопрос надо выяснить, что больше: 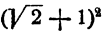 ? Допустим, что
? Допустим, что
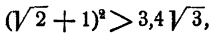
т. е.
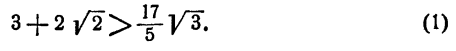
Тогда (теорема 4)
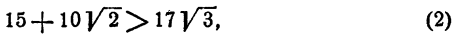
отсюда (теорема 7)
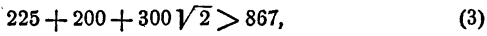
отсюда (теорема 3)

отсюда (теорема 4)

Мы показали, что из неравенства (1) следует неравенство (5). Но неравенство (5) несправедливо. Значит, нельзя предполагать, что неравенство (1) справедливо и таким образом
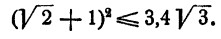
Далее,
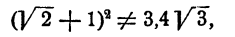
иначе 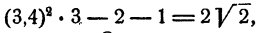 т. е. рациональное число равно иррациональному. Остается, что
т. е. рациональное число равно иррациональному. Остается, что
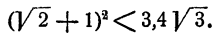
Корни квадратного уравнения
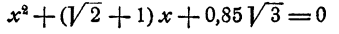
мнимые.
Ответ. Корни мнимые.
Пример:
Доказать, что, если а > 0, b > 0, то
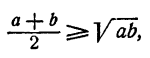
т. е. что среднее арифметическое двух положительных чисел не меньше их среднего геометрического.
Решение:
Допустим, что утверждение неверно, т. е.
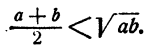
Тогда (теорема 7)
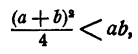
отсюда (теорема 4)
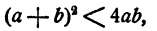
отсюда (теорема 3)
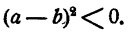
Последнее неравенство несправедливо. Значит, нельзя было предполагать, что утверждение неверно.
Проведенное в последнем примере рассуждение имеет несколько неестественный характер. Применялось доказательство от противного вместо естественного здесь прямого доказательства. Однако при решении задач на доказательство неравенств прямым способом часто допускаются ошибки в изложении, так как здесь легко спутать прямое утверждение с обратным.
Мы изложим два варианта прямого доказательства. Первый из них напоминает обычное рассуждение при решении геометрических задач на построение.
Анализ. Допустим, что задача решена и доказано, что

Тогда

Анализ показал, что из неравенства (6) вытекает неравенство (9). Неравенство (9) справедливо, но отсюда еще не следует, что справедливо неравенство (6). Однако если удастся доказать, что из неравенства (9) следует неравенство (6), то задача будет решена. Путь такого доказательства указан анализом.
Доказательство:
На основании теоремы 3 из неравенства (9) следует неравенство (8). На основании теоремы 4 из неравенства (8) следует неравенство (7). На основании теоремы 8 из неравенства (7) следует неравенство (6). Этим показано, что из неравенства (9) следует неравенство (6).
При желании можно анализ не излагать, а вести прямо доказательство. Очевидно, что
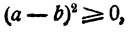
т е.
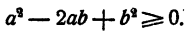
Прибавим к каждой части неравенства 4ab, получим
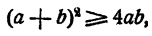
отсюда на основании теоремы 8
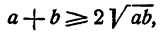
на основании теоремы 4
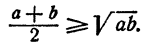
Ограничиваться же изложением одного анализа нельзя, так как из того, что некоторое утверждение справедливо, вообще не следует, что справедливо я обратное.
Второй вариант изложения ведется в форме, весьма напоминающей анализ, и является все же строгим. Требуется доказать, что

На основании теоремы 8 (но не 7) неравенство (10) вытекает из неравенства

На основании теоремы 4 неравенство (11) вытекает из неравенства

На основании теоремы 3 неравенство (12) вытекает из неравенства

Неравенство (13) очевидно.
Вычисления здесь приведены в том же порядке, что и при анализе, но всякий раз доказывалось, что доказываемое неравенство (10) вытекает из следующих за ним. При анализе поступают наоборот: из доказываемого неравенства (10) выводят все следующие за ним.
Замечание:
Рассмотренное неравенство имеет весьма простой геометрический смысл. На прямой АВ отложим последовательно отрезки а и b, на их сумме, как на диаметре, опишем окружность.
Тогда 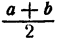 радиус этой окружности, а
радиус этой окружности, а 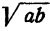 — половина хорды, перпендикулярной к диаметру в общей точке отрезков а b.
— половина хорды, перпендикулярной к диаметру в общей точке отрезков а b.
Пример:
Доказать, что при любом натуральном n
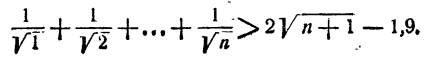
Доказательство:
При n = 1 неравенство справедливо, так как
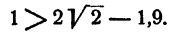
Предположим, что неравенство справедливо при n = k, где k — некоторое натуральное число, т. е.
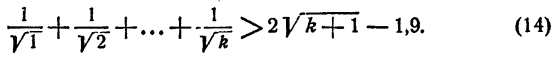
Докажем, что тогда неравенство справедливо и при n = k—1, т. е.
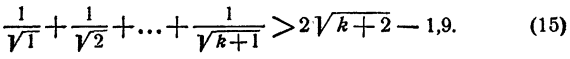
Сравнивая неравенства (14) и (15), заключаем, что неравенство (15) будет доказано, если будет установлено, что
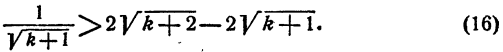
Действительно, сложив почленно неравенства (14) и (16), получим неравенство (15).
Остается доказать неравенство (16). Оно вытекает из неравенства
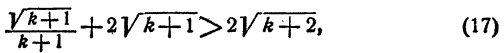
или
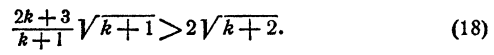
Неравенство (18) вытекает из неравенства
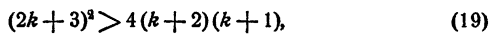
или
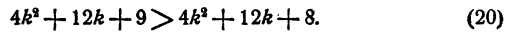
Неравенство (20) вытекает из очевидного неравенства 9 > 8.
Пример:
Доказать, что
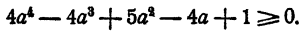
Доказательство:
Разложим левую часть неравенства на множители. Имеем
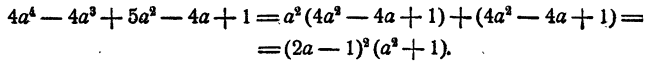
Так как
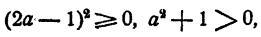
то
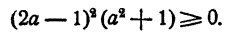
Равенство здесь имеет место только тогда, когда 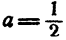
Пример:
Доказать, что при 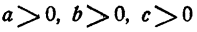
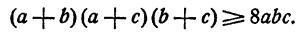
Доказательство:
Допустим, что с не превосходит а и b. Положим а = с + х, b = с + у, где х ≥ 0, у ≥ 0. Тогда неравенство можно переписать так:
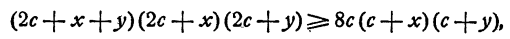
или
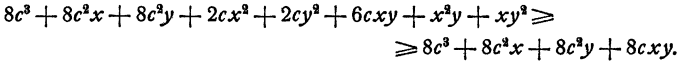
Последнее неравенство вытекает из неравенства
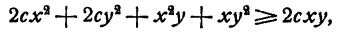
которое в свою очередь вытекает из очевидного неравенства
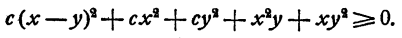
Точно так же можно доказать, что неравенство справедливо и тогда, когда b не превосходит с и а или а не превосходит b и с, так как буквы а, b, с входят в условие задачи симметрично.
Пример:
Доказать, что при n > 1
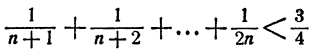
Доказательство:
Обозначим левую часть неравенства Sn. Имеем
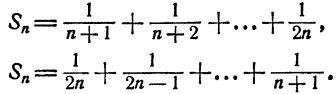
Второй раз слагаемые S расположены в порядке возрастания. Складывая почленно, имеем:
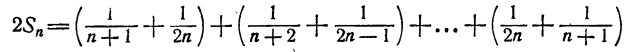
Если доказать, что при любом натуральном k, не превосходящем n,
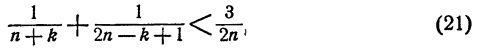
тогда получим, что
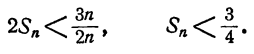
Остается доказать неравенство (21). Оно следует из неравенства
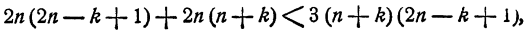
или, что все равно, из неравенства
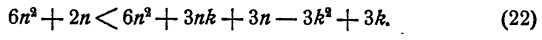
Неравенство (22) следует из неравенства
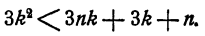
Последнее неравенство очевидно, так как
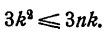
Пример:
Доказать, что если
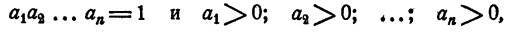
то
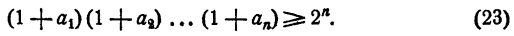
Доказательство:
По доказанному на стр. 445
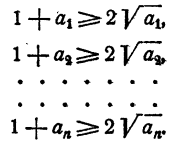
Перемножив неравенства почленно, имеем:
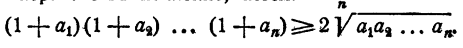
Учитывая, что 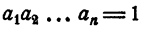 получим неравенство (23).
получим неравенство (23).
Равносильные неравенства
Неравенством с одним неизвестным называется неравенство вида
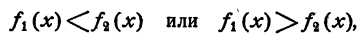
где f₁(x) и f₂(х) обозначают алгебраические выражения, содержащие неизвестное х. В частном случае одно из этих выражений может не содержать х. Например,

есть неравенство с одним неизвестным. Неравенство

также есть неравенство с одним неизвестным.
Определение:
Решить неравенство с одним неизвестным — это значит найти все значения неизвестного, при которых неравенство справедливо. Значения неизвестного, при которых неравенство справедливо, называются решениями неравенства.
Например, x =1 есть решение неравенства (1), так как при х = 1 это неравенство превращается в справедливое неравенство 5 > 2; 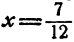 не является решением неравенства (2), так как при
не является решением неравенства (2), так как при 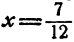 левая часть неравенства (2) принимает отрицательное значение
левая часть неравенства (2) принимает отрицательное значение 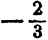
Определение:
Два неравенства называются равносильными, если каждое решение первого из них является решением второго, а каждое решение второго является решением первого.
Теорема:
Если к каждой части неравенства прибавить одно и то же число или один и тот же многочлен относительно неизвестного, то полученное в результате этого неравенство равносильно данному.
Доказательство:
Для упрощения изложения доказательство проведем применительно к неравенству
Все сказанное по поводу этого неравенства может быть повторено и по поводу любого другого неравенства.
Прибавим к каждой части неравенства какой-нибудь многочлен относительно неизвестного, например 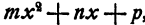 , получим неравенство
, получим неравенство
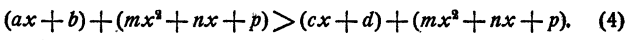
Требуется доказать, что неравенства (3) и (4) равносильны. Пусть х = х₀ есть решение неравенства (3), т. е.

— справедливое неравенство. К каждой части неравенства (5) прибавим число 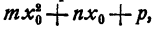 , получим (теорема 3 § 1) справедливое неравенство
, получим (теорема 3 § 1) справедливое неравенство
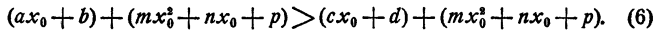
Неравенство (6) означает, что х = х₀ есть решение неравенства (4).
Итак, каждое решение неравенства (3) является решением неравенства (4).
Пусть теперь х = х₀ есть решение неравенства (4), тогда справедливо неравенство (6). На основании теоремы 3 § 1 справедливо и неравенство (5). Неравенство (5) означает, что х = х₀ есть решение неравенства (3).
Итак, каждое решение неравенства (4) является решением неравенства (3).
При. доказательстве теоремы мы не пользовались никакими особенностями многочлена 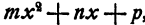 . Существенно было только то, что при любом значении х многочлен этот имеет определенное числовое значение. Поэтому доказательство остается в силе и тогда, когда к каждой части неравенства (3) прибавляется какой-нибудь другой многочлен относительно х. В частности, доказательство остается в силе, когда к каждой части неравенства (3) прибавляется какое-нибудь число (многочлен нулевой степени относительно х).
. Существенно было только то, что при любом значении х многочлен этот имеет определенное числовое значение. Поэтому доказательство остается в силе и тогда, когда к каждой части неравенства (3) прибавляется какой-нибудь другой многочлен относительно х. В частности, доказательство остается в силе, когда к каждой части неравенства (3) прибавляется какое-нибудь число (многочлен нулевой степени относительно х).
Замечание:
Если бы к каждой части неравенства прибавили не многочлен относительно х, а какое-нибудь выражение, содержащее неизвестное в знаменателе, полученное в результате этого неравенство могло бы оказаться и неравносильным данному. Например, неравенство 2х — 1 > 0 имеет решение х = 3. Неравенство
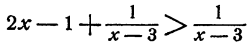
при x = 3 не имеет смысла.
Следствие:
Любое слагаемое можно перенести из одной части неравенства в другую, изменив при этом знак его на противоположный.
Доказательство опять проведем применительно к неравенству
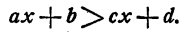
Предположим, что желательно слагаемое сх перенести из правой части неравенства в левую. Прибавим к каждой части неравенства по —сх, получим равносильное неравенство
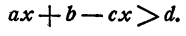
Слагаемое сх с противоположным знаком перенесено из правой части неравенства в левую.
Теорема:
Если обе части неравенства умножить на одно и то же положительное число, то полученное в результате этого неравенство равносильно данному.
Если обе части неравенства умножить на одно и то же отрицательное число и при этом переменить знак неравенства на знак противоположного смысла, то полученное в результате этого неравенство равносильно данному.
Доказательство:
Доказательство и здесь проведем применительно к неравенству (3)
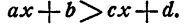
Умножим обе части этого неравенства на положительное число m получим
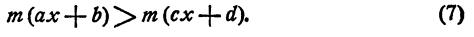
Пусть х = х₀ — решение неравенства (3), т. е.

— справедливое неравенство. Тогда на основании теоремы 4 § 1 справедливо и неравенство
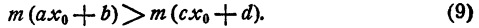
Неравенство (9) означает, что х = х₀ есть решение неравенства (7).
Итак, каждое решение неравенства (3) является решением неравенства (7).
Пусть теперь х = х₀ есть решение неравенства (7), тогда справедливо неравенство (9). На основании теоремы 4 § 1 справедливо и неравенство (8), и это означает, что х = х₀ есть решение неравенства (3).
Итак, каждое решение неравенства (7) является решением неравенства (3).
Первая часть теоремы доказана. Точно так же доказывается и вторая часть теоремы относительно умножения обеих частей неравенства на одно и то же отрицательное число.
Замечание:
При умножении обеих частей неравенства на буквенное выражение надо иметь в виду, что при разных значениях входящих в него букв это выражение может быть и положительным, и отрицательным, и равным нулю.
Решение неравенств и систем неравенств первой степени с одним неизвестным
Определение:
Неравенством первой степени с одним неизвестным называется такое неравенство, которое после раскрытия скобок, приведения подобных членов и перенесения всех членов в левую часть принимает вид ах + b > 0 или ах + b < 0
Умножением обеих частей неравенства ах + b < 0 на —1 его можно привести к равносильному неравенству вида
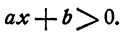
Поэтому достаточно изучить только неравенство ах + b > 0
Теорема:
Если а ≠ 0, то неравенство

имеет бесконечное множество решений, именно, ему удовлетворяют все числа, большие 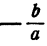 , когда а > 0, и меньшие
, когда а > 0, и меньшие 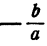 , когда а < 0.
, когда а < 0.
Если а = 0, неравенство (1) не имеет решений, когда b ≤ 0, и имеет бесконечное множество решений, когда b>0. В последнем случае ему удовлетворяет любое число.
Доказательство:
Неравенство (1) равносильно неравенству

Пусть a > 0, тогда неравенство (2) равносильно неравенству

Последнее неравенство — простейшее, ему удовлетворяют все числа, которые больше чем 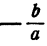 , и только эти числа.
, и только эти числа.
Пусть а < 0, тогда неравенство (2) равносильно неравенству

Неравенство (4) — простейшее, ему удовлетворяют все числа, которые меньше чем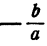 , и только эти числа.
, и только эти числа.
Пусть а = 0. Неравенство (1) принимает вид 0x + b > 0 Это неравенство не имеет решений, когда b ≤ 0 и имеет бесконечное множество решений, когда b > 0. В этом случае неравенству удовлетворяет любое значение х.
Пример:
Решить неравенство 2х — 3 > x—1.
Решение:
Переносим неизвестные в левую часть, а известные в правую, имеем х > 2.
Полученному неравенству удовлетворяют все числа, бoльшие 2, и только эти числа. Решения неравенства изображаются точками, лежащими правее точки 2 (рис. 98).
Ответ, х >2.
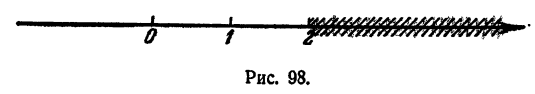
Пример:
Решить неравенство
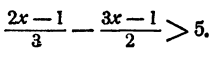
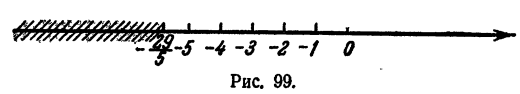
Решение:
Умножим обе части неравенства на 6, получим
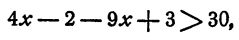
отсюда
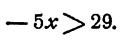
Разделим обе части неравенства на -5 (умножим на 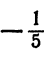 )
)
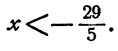
Решения неравенства (рис. 99) изображаются точками числовой оси,
лежащими левее точки 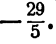
Ответ. 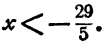
К неравенствам первой степени иногда сводятся неравенства, содержащие неизвестное в знаменателе.
Пример:
Решить неравенство

Решение:
Для освобождения неравенства от дробей обе части его надо умножить на х — 1. Очевидно, х — 1 ≠ 0, так как иначе неравенство (5) не имеет смысла. Так как х—1 может быть и положительным и отрицательным, приходится рассмотреть два случая.
Случай 1. Пусть х — 1 > 0, т. е. x > 1. Тогда
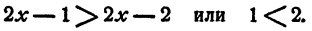
Этому неравенству удовлетворяет любое значение х. Таким образом, неравенству (5) удовлетворяет любое значение х > 1.
Случай 2. Пусть x < 1, тогда
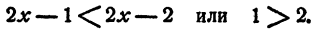
Это неравенство решений не имеет.
Ответ. х > 1.
При решении неравенств с буквенными коэффициентами необходимо учитывать знак коэффициента при неизвестном.
Пример:
Решить неравенство
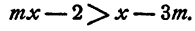
Решение:
Перенесем неизвестные в левую часть, а известные в правую, получим
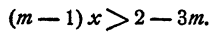
Так как m— 1 может быть и положительным числом, и нулем, и отрицательным числом, приходится рассмотреть три случая.
Случай 1. m > 1. Тогда
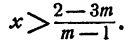
Случай 2. m = 1. Неравенство принимает вид
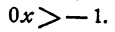
Это неравенство справедливо при любом х.
Случай 3. m < 1. Тогда
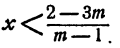
Ответ. Если m > 1,то 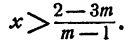 ; если m = 1, то неравенство справедливо при любом значении х; если m < 1, то
; если m = 1, то неравенство справедливо при любом значении х; если m < 1, то 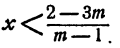
Определение:
Два или несколько неравенств с одним неизвестным образуют систему неравенств, если неизвестное в них обозначает одну и ту же величину. Решить систему неравенств с одним неизвестным — это значит найти все значения неизвестного, при которых все неравенства системы справедливы.
Пример:
При каком значении х дробь

положительна?
Решение:
Чтобы дробь была положительна, необходимо и достаточно, чтобы числитель и знаменатель были одного знака. Поэтому задача сводится к решению двух систем неравенств

и

Первое неравенство системы (7) требует, чтобы 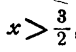 , второе —
, второе —
чтобы 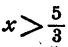 . Так как
. Так как 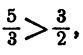 системе (7) удовлетворяют все значения
системе (7) удовлетворяют все значения 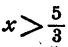 и только эти значения.
и только эти значения.
Первое неравенство системы (8) требует, чтобы 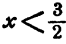 второе—чтобы
второе—чтобы 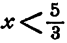 При
При 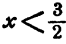 и только при этих значениях х удовлетворяются оба неравенства системы (8).
и только при этих значениях х удовлетворяются оба неравенства системы (8).
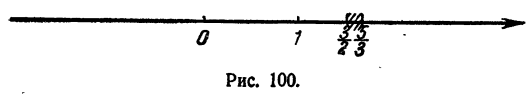
Таким образом, дробь (6) положительна при 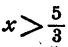 и при
и при 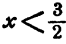 Геометрически это означает, что дробь (6) положительна в любой точке числовой оси, кроме точек, лежащих внутри и на концах отрезка
Геометрически это означает, что дробь (6) положительна в любой точке числовой оси, кроме точек, лежащих внутри и на концах отрезка 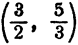 , (рис. 100).
, (рис. 100).
Пример:
Решить систему неравенств
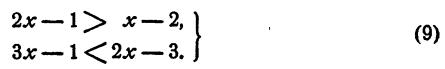
Решение:
Первое неравенство требует, чтобы х > — 1. Второе неравенство требует, чтобы х <- 2. Система (9) решений не имеет, так как нет такого числа, которое было бы больше — 1 и меньше- 2.
Цель исследования уравнений
Решение задач при помощи уравнений приводит иногда к результату, который показывает, что данная задача, не имеет решений. Часто такой вывод делается потому, что уравнение, составленное по условию задачи, не имеет, решений. Иногда же оказывается, что уравнение имеет решения, но решения эти не удовлетворяют условию задачи.
Если в условии задачи некоторые из данных величин обозначены буквами, т. е. ищется решение задачи в общем виде, уравнение, составленное по условию задачи, имеет буквенные коэффициенты. Такое уравнение при одних частных значениях букв имеет решение, при других значениях букв оно решений не имеет. При одних значениях букв решения удовлетворяют условию задачи и дают ответы на вопрос задачи, при других значениях букв решения условию задачи не удовлетворяют.
В силу этого при решении задач с буквенными данными требуется провести исследование задачи, т. е. выяснить:
1) при каких значениях букв уравнение или система уравнений имеет решения, и если имеет, то сколько;
2) при каких значениях букв решения уравнения или системы уравнений удовлетворяют условию задачи и при каких значениях букв решения условию задачи не удовлетворяют.
Ответ на первый из поставленных вопросов требует умения исследовать уравнение или систему уравнений с буквенными коэффициентами, независимо от того, что представляют собой величины, обозначенные буквами.
Ответ на второй вопрос требует умения отобрать из всех решений те, которые удовлетворяют условию задачи.
Исследование уравнения первой степени с одним неизвестным
Уравнение первой степени с одним неизвестным может быть преобразовано к виду
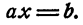
Теорема:
Если коэффициент при неизвестном в уравнении первой степени с одним неизвестным отличен от нуля, уравнение имеет решение и притом единственное.
Если коэффициент при неизвестном в уравнении первой степени с одним неизвестным равен нулю, уравнение не имеет решений, когда свободный член отличен от нуля, и имеет бесконечное множество решений, когда свободный член равен нулю. В последнем случае уравнению удовлетворяет любое число.
Доказательство:
Если а ≠ 0, уравнение ах = b равносильно уравнению 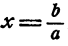 . Это уравнение простейшее, ему удовлетворяет число
. Это уравнение простейшее, ему удовлетворяет число 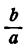 — и только это число.
— и только это число.
Если а = 0, уравнение ах = b принимает вид 0х = b. Это уравнение не имеет решений, когда b отлично от нуля, так как произведение нуля и любого числа равно нулю. Если же b = 0, это уравнение принимает вид 0x = 0. Такому уравнению удовлетворяет любое значение х.
Задача:
Два фонтана наполняют бассейн: первый, действуя один, может наполнить бассейн в а часов; второй, будучи открыт один, наполнит бассейн в b часов. Кран, находящийся в дне бассейна, может опорожнить бассейн в с часов. Во сколько часов бассейн, вначале пустой, будет наполнен, если оба фонтана и кран будут открыты одновременно?
Решение:
Пусть бассейн наполняется в х часов. Первый фонтан, наполняя весь бассейн в а часов, в один час наполняет 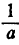 часть бассейна, а в х часов
часть бассейна, а в х часов 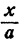 частей его. Второй фонтан за х часов наполняет
частей его. Второй фонтан за х часов наполняет 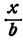 частей бассейна. Кран за х часов выпустит воду в объеме
частей бассейна. Кран за х часов выпустит воду в объеме 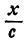 частей бассейна. Так как разность между приходом и расходом воды за х часов равна емкости бассейна, имеем уравнение
частей бассейна. Так как разность между приходом и расходом воды за х часов равна емкости бассейна, имеем уравнение
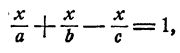
откуда
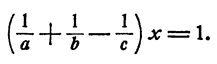
Если 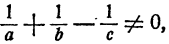 Уравнение имеет единственное решение
Уравнение имеет единственное решение
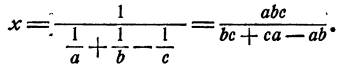
Если 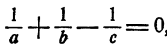 уравнение решений не имеет.
уравнение решений не имеет.
По смыслу задачи, х должно быть положительным числом, и потому задача имеет решение только тогда, когда
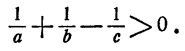
Нетрудно видеть, что неравенство 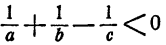 означает, что количество воды, доставляемое в 1 час двумя фонтанами, меньше количества воды, которую способен выпустить кран в течение часа.
означает, что количество воды, доставляемое в 1 час двумя фонтанами, меньше количества воды, которую способен выпустить кран в течение часа.
Равенство 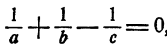 означает, что количество воды, доставляемой двумя фонтанами в 1 час, равно количеству воды, выпускаемой краном за то же время.
означает, что количество воды, доставляемой двумя фонтанами в 1 час, равно количеству воды, выпускаемой краном за то же время.
Ясно поэтому, что в случаях, когда 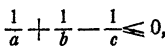 , задача не имеет решения.
, задача не имеет решения.
Ответ. В 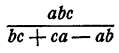 часов; задача имеет решение только тогда, когда
часов; задача имеет решение только тогда, когда 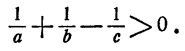
Исследование системы двух уравнений первой степени с двумя неизвестными
Основные определения.
1 Два или несколько уравнений образуют систему уравнений, если одноименные неизвестные в них обозначают одну и ту же величину.
2 Системой двух уравнений первой степени с двумя неизвестными называется система, которая после раскрытия скобок, перенесения членов, содержащих неизвестные, в левую часть, а известных членов в правую часть и приведения подобных членов принимает вид

где 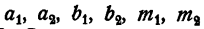 — известные числа.
— известные числа.
3 Решить систему (1) — это значит найти такие значения для х и у, которые, будучи поставлены в систему вместо неизвестных, превращают каждое уравнение системы в тождество.
4 Решением системы уравнений с двумя неизвестными называется пара таких чисел, которые, будучи подставлены в систему вместо неизвестных, превращают каждое уравнение системы в тождество.
5 Исследовать систему (1) — это значит по коэффициентам ее определить, имеет ли система решения, и если имеет, то сколько.
6 Система (1) называется приведенной, если оба коэффициента при одном неизвестном в ней равны 1. Например, системы
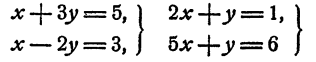
— приведенные. Система
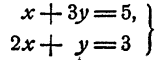
не является приведенной.
Теорема:
Если оба коэффициента при каком-нибудь неизвестном в системе (1) отличны от нуля, то систему amy можно привести, т. е. построить равносильную ей приведенную систему.
Доказательство:
Пусть a₁ ≠ 0 и а₂, ≠ 0.
Разделим обе части первого уравнения на a₁, обе части второго уравнения на а₂ Получим приведенную систему, равносильную данной. (При делении обеих частей уравнения на одно и то же число ни одно решение не теряется и ни одно решение не приобретается.)
Точно так же доказывается теорема, если b₁ ≠ 0 и b₂ ≠ 0.
Теорема:
Если в приведенной, системе левые части различны, система имеет решение и притом единственное.
Доказательство:
Дана приведенная система

причем p₁ ≠ p₂
Предположим, что система (2) имеет решение, т. е. предположим, что существуют такие два числа 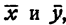 , что имеют место тождества
, что имеют место тождества
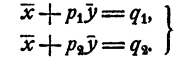
Умножим первое тождество на р₂ второе на — р₁ и сложим их почленно. Получим
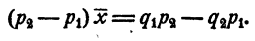
Отсюда
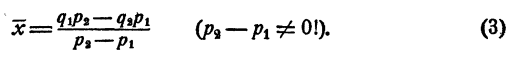
Из второго тождества вычтем первое, получим
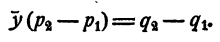
Отсюда
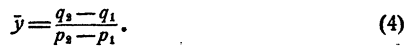
Какой вывод мы можем сделать?
Вывод. Если система (2) имеет решение, то решение это определяется по формулам (3) и (4), а потому единственно.
Действительно, допустим, что система (2) имеет другое решение 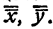
Тогда имеют место тождества
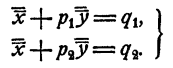
Рассуждая так же, как и выше, получим
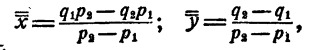
т. е.
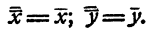
Докажем, что х и у, определяемые формулами (3) и (4), удовлетворяют системе (2). Для этого достаточно в систему (2) подставить вместо х и у их значения по формулам (3) и (4) и убедиться, что каждое уравнение системы превращается в тождество.
Теорема:
Если в приведенной системе левые части одинаковы, а правые различны, система решений не имеет.
Доказательство:
Имеем систему

причем q₁ ≠ q₂. Система (5) не может иметь решений, так как не может существовать такая пара чисел х и у, чтобы х + pу равнялось одновременно и q₁ , и q₂ .
Теорема:
Если в приведенной системе и левые и правые части одинаковы, система имеет бесконечное множество решений.
Доказательство:
Имеем систему

Уравнение x + py = q имеет бесконечное множество решений. Каждое такое решение является и решением системы (6).
Правило:
Для того чтобы узнать, сколько решений имеет данная система двух уравнений первой степени с двумя неизвестными, достаточно систему привести. Если в приведенной системе левые части различны, система имеет решение и притом только одно. Если же в приведенной системе левые части одинаковы, система не имеет решений, когда правые части различны, и имеет бесконечное множествo решений, когда правые части тоже одинаковы.
Пример:
Исследовать системы
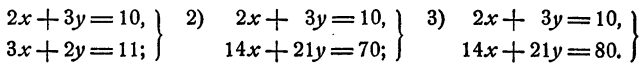
Решение:
Приведем каждую из систем, получим
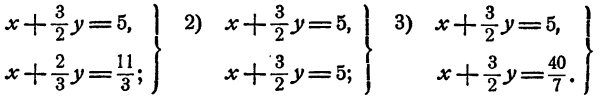
Первая система имеет единственное решение. Вторая имеет бес-конечное множество решений: 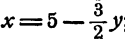 у—любое число. Третья не имеет решений.
у—любое число. Третья не имеет решений.
Пример:
Показать, что при любом b система
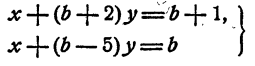
имеет единственное решение.
Решение:
Уравнение b + 2 = b— 5 не имеет решений. Поэтому при любом b левые части системы различны. Пример. Исследовать систему
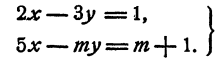
Решение:
Приведем систему, получим:
Если 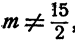 , система имеет единственное решение. Если
, система имеет единственное решение. Если 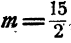
система имеет вид
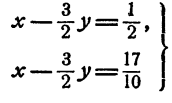
и решений не имеет.
Рассмотрим теперь системы, которые не могут быть приведены. Нетрудно видеть, что такие системы могут быть отнесены к одному из следующих четырех типов:
Тип 1. Система имеет такой вид:
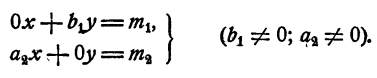
Тип 2.Система имеет такой вид:
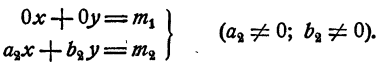
Тип 3. Система имеет такой вид:
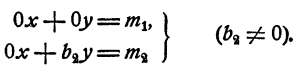
Тип 4. Система имеет такой вид:
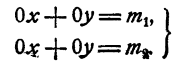
Система типа 1 имеет единственное решение:
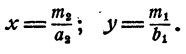
Действительно, первое уравнение системы имеет решение 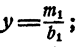 х — любое число; второе уравнение системы имеет решение
х — любое число; второе уравнение системы имеет решение 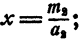 у— любое число.
у— любое число.
Система типа 2 не имеет решений, если m₁ ≠ 0, и имеет бесконечное множество решений, если m₁ = 0. В последнем случае
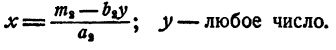
Система типа 3 не имеет решений, если m₁ ≠ 0 , и имеет бесконечное множество решений, если m₁ = 0 . В последнем случае
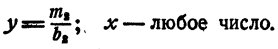
Система типа 4 не имеет решений, если хоть одно из чисел m₁ и m₂ отлично от нуля. Если же m₁ = m₂ = 0, система имеет бесконечное множество решений: х — любое число; у — любое число.
Определение:
Выражение a₁ b₂ — a₂ b₁ называется определителем системы
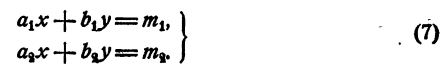
Теорема:
Если определитель системы отличен от нуля и система эта может быть приведена, то отличен от нуля также и определитель соответствующей приведенной системы. Если определитель системы равен нулю и система эта может быть приведена, то равен нулю также и определитель соответствующей приведенной системы.
Доказательство:
Пусть a₁≠0; a₂≠ 0 Приведем систему (7), получим
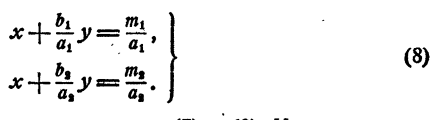
Пусть D₁ и D₂ — определители систем (7) и (8). Имеем
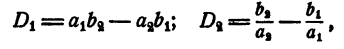
т.е. D₁ = a₁a₂D₂.Если D₁ ≠ 0,то и D₂ ≠ 0.Если D₁ = 0,то и D₂ = 0.
Теорема:
Если определитель системы отличен от нуля, система имеет решение и притом единственное. Если определитель системы равен нулю, система либо совсем не имеет решений, либо имеет их бесконечное множество.
Доказательство:
Все изложенное выше может быть сведено в таблицу (см. табл. 1), из которой видно, что система имеет единственное решение тогда и только тогда, когда определитель ее отличен от нуля. Система не имеет решений или имеет их бесконечное множество тогда и только тогда, когда определитель ее равен нулю.
Таблица 1

Теоремы о решении систем двух уравнений первой степени с двумя неизвестными могут быть выведены и без рассмотрения приведенных систем.
Теорема:
Если a₁ b₂ — a₂ b₁ ≠0 , то система

имеет решение и притом единственное.
Доказательство:
Допустим, что система (9) имеет решение, что решение это найдено и вместо неизвестных подставлено в гсистему. Тогда каждое уравнение системы превратится в тождество. Умножим первое тождество на b₂ второе на — b₁ и сложим. Получим
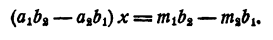
Так как

Вернемся к тождествам (9). Первое из них умножим на — a₂ , второе на a₁ , и сложим. Получим
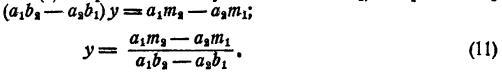
Из сказанного вытекает, что если система (9) имеет решение, то решение это определяется формулами (10) и (11), и следовательно, единственное.
Остается доказать, что система (9) действительно имеет решение. Для этого достаточно в систему (9) подставить вместо х и у их значения по формулам (10) и (11) и убедиться, что каждое из уравнений системы (9) превращается в тождество.
Теорема:
Если a₁b₂ — a₂b₁ = 0, то система
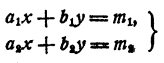
либо совсем не имеет решений, либо имеет их бесчисленное множество. Доказательство этой теоремы разобьем на два случая. Случай 1. Все коэффициенты при неизвестных а₁ а₂, b₁b₂, отличны от нуля. Перепишем систему так:
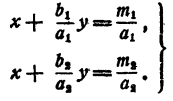
По условию, a₁b₂ — a₂b₁ = 0 , значит, 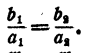 Поэтому, если
Поэтому, если 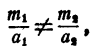 то система не имеет решения, если же
то система не имеет решения, если же 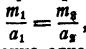 , то система имеет бесчисленное множество решений. Всякое решение одного из уравнений является решением системы.
, то система имеет бесчисленное множество решений. Всякое решение одного из уравнений является решением системы.
Случай 2. Среди коэффициентов при неизвестных имеются нули. Здесь возможны следующие случаи:
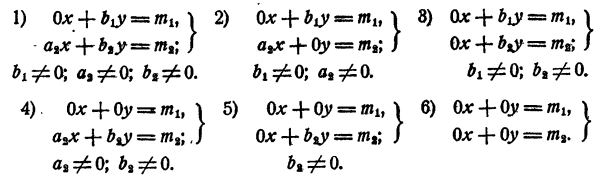
Случаи 1) и 2) отпадают, так как здесь a₁ b₂ — a₂ b₁ ≠0 . В случае 3) первое уравнение имеет решения х— любое число, а , второе уравнение имеет решения х—любое число, а
, второе уравнение имеет решения х—любое число, а 
Если  , то система решений не имеет. Если же
, то система решений не имеет. Если же 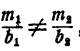 , то система имеет бесчисленное множество решений х — любое число;
, то система имеет бесчисленное множество решений х — любое число;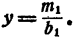
Случаи 4), 5) и 6) подробно рассмотрены на стр. 462. Изложенный здесь вывод короче вывода, данного в начале параграфа, но он формальнее и хуже выясняет суть дела.
Пример:
Исследовать систему
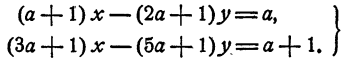
Решение:
Вычислим определитель системы:
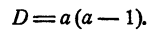
Если а ≠ 0 и а ≠ 1, система имеет единственное решение:
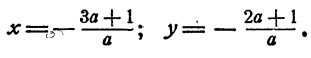
Если а = 0, система имеет вид
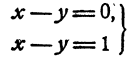
и решений не имеет.
Если а = 1, система имеет вид
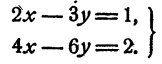
Приведем систему, получим
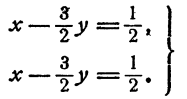
Система имеет бесконечное множество решений:  ; у — любое число.
; у — любое число.
Ответ. Если а(а — 1) ≠ 0, система имеет единственное решение. Если а = 0, система решений не имеет. Если а = 1, система имеет бесконечное множество решений.
Задача:
Две группы лыжников общей численностью в 100 человек выделили сборную команду в 15 человек. Первая группа выделила своего состава, вторая группа выделила 10% своего состава. Сколько лыжников в каждой группе?
Решение:
Пусть в первой группе х лыжников, во второй у лыжников. Тогда
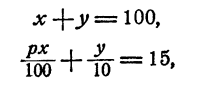
или
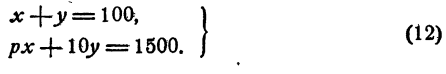
Определитель системы (12) равен 10—р. Если р = 10, система (12) принимает вид
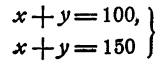
и решений не имеет.
Если p ≠ 10 система имеет единственное решение
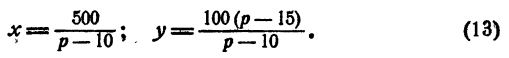
Так как х должно быть положительным, p > 10. Так как у должен быть положительным, p > 15
Из этого видно, что при p ≤ 15 решение (13) не удовлетворяет условию задачи. С другой стороны,p ≤ 100. Таким образом,
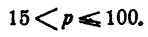
Отсюда

Так как х должно быть целым числом, то 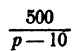 целое, следовательно, число р —10 должно быть делителем числа 500.
целое, следовательно, число р —10 должно быть делителем числа 500.
500 = 2² • 5³, поэтому для получения всех делителей числа 500 достаточно каждое из чисел 1, 2, 2² умножить на каждое из чисел 1, 5, 5², 5³. Получаем, что число 500 имеет 12 делителей: 1, 2, 4, 5, 10, 20, 25, 50, 100, 125, 250 и 500.
Согласно неравенству (14) для р —10 возможны только следующие значения: 10, 20, 25, 50, и следовательно, для р возможны только значения 20, 30, 35 и 60.
По условию, 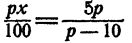 должно быть целым числом. Этому требованию удовлетворяют следующие значения р: 20, 35 и 60. Значениеp = 30 этому требованию не удовлетворяет. Окончательно имеем следующую таблицу решений:
должно быть целым числом. Этому требованию удовлетворяют следующие значения р: 20, 35 и 60. Значениеp = 30 этому требованию не удовлетворяет. Окончательно имеем следующую таблицу решений:
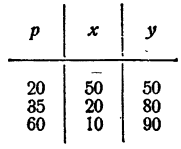
Ответ. В первой группе либо 50, либо 20, либо 10 лыжников.
Исследование квадратного трехчлена
Содержание этого параграфа является дальнейшим развитием тех сведений, которые изложены в § 7 гл. II.
Теорема:
Если дискриминант квадратного трехчлена отрицателен, трехчлен при всех значениях независимого переменного имеет тот же знак, что и его старший коэффициент.
Доказательство:
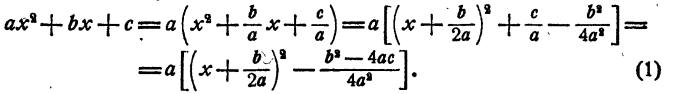
Так как b² — 4ас < 0, выражение в квадратных скобках представляет собой сумму квадрата и положительного числа, т. е. при всех значениях х является положительным числом. В силу этого трехчлен имеет при всех значениях х тот же знак, что и коэффициент а.
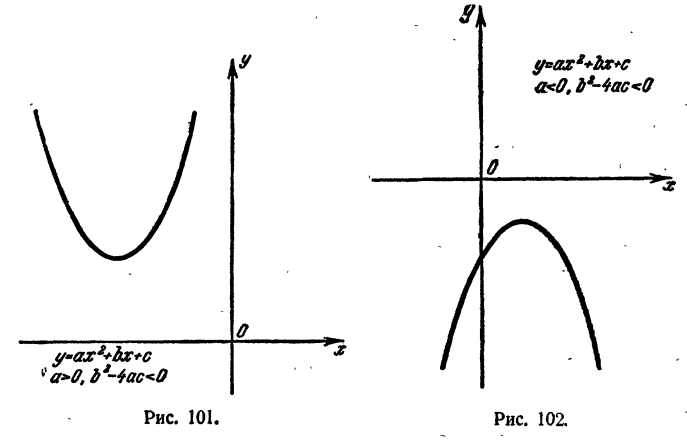
Доказанная теoрема имеет следующий геометрический смысл.
Если дискриминант квадратного трехчлена отрицателен, график его целиком расположен в верхней полуплоскости (т. е. в полуплоскости, в которой ординаты положительны), когда 0, и в нижней полуплоскости, когда а < 0. Напомним, что график квадратного трехчлена называется параболой (рис. 101 и 102).
Теорема:
Если дискриминант квадратного трехчлена равен нулю, трехчлен равен нулю при 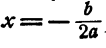 а при всех остальных значениях независимого переменного имеет тот же знак, кто и его старший коэффициент.
а при всех остальных значениях независимого переменного имеет тот же знак, кто и его старший коэффициент.
Доказательство:
При b² — 4ас < 0 равенство (1) принимает вид
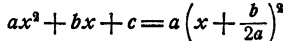
Выражение 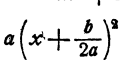 равно нулю при
равно нулю при 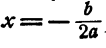 а при остальных значениях х имеет тот же знак, что и а.
а при остальных значениях х имеет тот же знак, что и а.
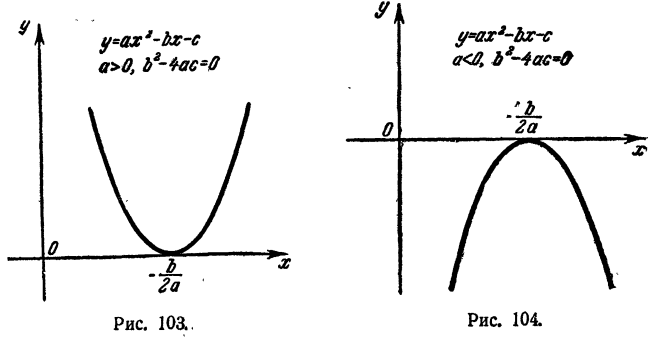
Доказанная теорема имеет следующий геометрический смысл. Если дискриминант квадратного трехчлена равен нулю, график его касается оси Ох в точке 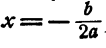 и расположен в верхней полуплоскости, когда a > 0, и в нижней . полуплоскости, когда а< 0 (рис. 103 и 104).
и расположен в верхней полуплоскости, когда a > 0, и в нижней . полуплоскости, когда а< 0 (рис. 103 и 104).
Теорема:
Если дискриминант квадратного трехчлена положителен, трехчлен обращается в нуль в двух различных точках x₁ и x₂. Во всех точках, лежащих вне промежутка (x₁, х₂), трехчлен имеет знак своего старшего коэффициента, а во всех точках внутри этого промежутка имеет знак, противоположный знаку старшего коэффициента.
Доказательство:
Трехчлен обращается в нуль при х = х₁ и x = x₂ причем x₁ ≠ х₂.
Пусть х₁ < х₂ .Выясним сначала знак трехчлена вне промежутка (xx) т. е. при x < х₁ и при x > х₂
Если x < х₁ то x > х₂ и произведение (x- х₁ ) (x- х₂ )положительно. Значит, правая часть равенства (2) имеет тот же знак, что и коэффициент а.
Если x > х₂ , то x > х₁ и произведение (x- х₁ ) (x- х₂ ) опять положительно и правая часть равенства (2) опять имеет тот же знак, что и коэффициент а.
Осталось рассмотреть, какой знак имеет трехчлен при х, лежащем внутри промежутка между корнями.
Пусть х₁ < х < х₂ В этом случае х — х₁ > 0, а х — х₂ < 0. Произведение (x- х₁ ) (x- х₂ ) — отрицательно, и правая часть равенства (2) имеет знак, противоположный знаку коэффициента а.
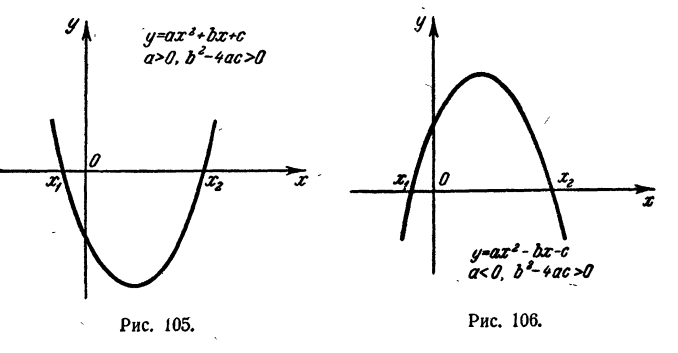
Доказанная теорема имеет следующий геометрический смысл. Если дискриминант квадратного трехчлена положителен, график его пересекает ось Ох в двух точках. Если при этом старший коэффициент трехчлена положителен, график трехчлена, за исключением дуги, отсекаемой осью Ох, находится в верхней полуплоскости. Если же старший коэффициент трехчлена отрицателен, график его, за исключением дуги, отсекаемой осью Ох, находится в нижней полуплоскости (рис. 105 и 106).
Задача:
Моторная лодка, пройдя по течению реки расстояние S км от пункта А до пункта В, повернула обратно в пункт А. Не доехав до Ар км, лодка остановилась. На весь путь от А до В и обратно до остановки лодка потратила t часов. Определить собственную скорость лодки (скорость в стоячей воде), если скорость течения реки а км/час.
Решение:
Пусть собственная скорость лодки равна х км/час. Тогда скорость лодки, идущей по течению, (x + a) км/час, скорость лодки, идущей против течения, (х — а) км/час.
Путь, пройденный лодкой по течению, S км. Путь, пройденный лодкой против течения, (S—р) км. Время движения лодки по течению  час. Время движения лодки против течения
час. Время движения лодки против течения 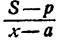 час.
час.
Так как лодка находилась в движении t часов, то получаем следующее уравнение:
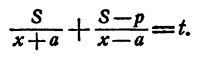
2. Посмотрим, какие ограничения для неизвестного и параметров вытекают из условия задачи. Собственная скорость лодки должна быть больше скорости течения реки, так как иначе лодка не сможет плыть против течения реки, следовательно, х > а. Очевидно, что
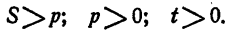
3. Составим систему уравнений и неравенств, которым должно удовлетворять решение задачи:
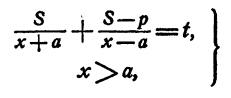
при условии S > p; р > 0; t > 0 .
4. Решим систему:
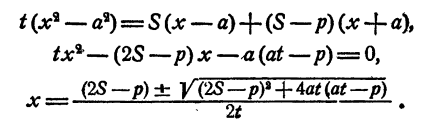
Теперь нужно выяснить, действительны ли корни квадратного уравнения и удовлетворяют ли они требованию х > а. С этой целью рассмотрим квадратный трехчлен
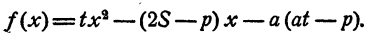
Определим знак трехчлена при х = а:
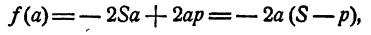
следовательно, f(a) < 0. Старший коэффициент t трехчлена положителен.
Из теорем, доказанных в этом параграфе, легко вывести утверждение: если квадратный трехчлен при х = а имеет отрицательное значение, а старший коэффициент трехчлена положителен, то дискриминант трехчлена положителен и число а находится между корнями трехчлена.
Поэтому корни x₁ и x₂ уравнения (3) действительны и
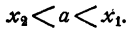
Бoльший корень уравнения удовлетворяет всем условиям задачи.
Если бы мы не пользовались свойствами квадратного трехчлена, то решение было бы сложнее. Тогда следовало бы представить дискриминант уравнения в виде
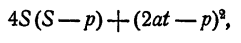
показать, что он положителен, и, кроме того, доказать, что x₁ > а; х₂ < a.
Ответ.
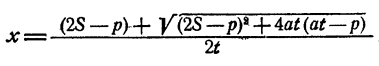
Решение неравенства второй степени с одним неизвестным
Неравенство второй степени с одним неизвестным имеет вид

или

Так как умножением обеих частей на —1 неравенство (2) превращается в неравенство вида (1), достаточно научиться решать неравенство (1).
Это проще всего сделать, исходя из графика квадратного трехчлена.
Действительно, для того чтобы решить неравенство (1), достаточно узнать, при каких значениях х график трехчлена находится в верхней полуплоскости. Ответ на этот вопрос можно дать на основании результатов исследования квадратного трехчлена.
Пусть D = b² — 4 ас.
- Если а > 0 и D > 0, график трехчлена находится в верхней полуплоскости, за исключением дуги, отсекаемой осью Ох. Неравенство (1) справедливо при x < x₁ и при где х₁ и x₂ корни трехчлена и x₁ < x₂
- Если а > 0 и D = 0, весь график трехчлена, за исключением одной точки, в которой он касается оси Ох, находится в верхней полуплоскости. Неравенство (1) справедливо при всех значениях х, кроме
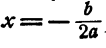
- Если а > 0 и D < 0, весь график трехчлена находится в верхней полуплоскости, и неравенство справедливо при всех значениях х.
- Если а < 0 и D > 0, график трехчлена находится в нижней полуплоскости, за исключением дуги, отсекаемой осью Ох. Неравенство (1) справедливо только при х₁ < x < x₂ где х₁ и x₂ — корни трехчлена.
- Если а < 0 и D = 0, весь график трехчлена, кроме точки касания с осью Ох, находится в нижней полуплоскости и неравенство (1) решений не имеет.
- Если а < 0 и D < 0, весь график трехчлена находится в нижней полуплоскости и неравенство (1) решений не имеет.
Полученные результаты коротко можно выразить так:
Если а > 0, то неравенству ах² + bx + с > 0 удовлетворяют все вещественные числа, за исключением корней трехчлена и чисел, заключенных между ними.
Если а < 0 то неравенству ах² + bx + с > 0 удовлетворяют все числа, заключенные между корнями трехчлена, и только они.
Пример:
Решить неравенство .
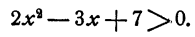
Решение:
D = 9 — 56 < 0. Трехчлен не имеет вещественных корней. Неравенство справедливо при всех значениях х.
Пример:
Решить неравенство

Решение:
Для освобождения неравенства от дроби обе части его нужно умножить на а — 2. Поэтому приходится рассмотреть два случая.
Случай 1. а > 2. Неравенство (1) принимает вид
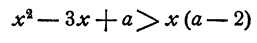
или
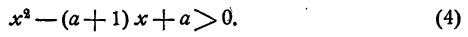
Левая часть неравенства (4) имеет корни х₁ = 1 и x₂ = a, причем x₁ < x₂ так как а >2. Неравенство (4) справедливо при всех значениях л:, лежащих вне промежутка (1, а), т. е. при х < 1 и при х > а.
Случай 2. а < 2. В этом случае неравенство (3) приводится к виду
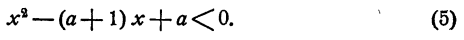
Левая часть неравенства (5) имеет корни х₁ = 1 ; x₂ = a . Неравенство (5) справедливо при всех значениях х, лежащих внутри промежутка, образованного корнями х₁ и x₂ . Рассмотрим три случая: а < 1; а = 1; а > 1.
Если а < 1 неравенство (5) справедливо при a < x < 1
Если а = 1, неравенство (5) решений не имеет.
Если а > 1. неравенство (5) справедливо при 1 < х < а < 2.
Ответ. Если а < 1,то a < x < 1 если а= 1, то неравенство решений не имеет; если 1< а < 2, то 1< x < а если a > 2, то x < 1 и х > а.
Общие сведения о неравенствах
Свойства неравенств:
Напомним, что из двух чисел а и b меньшим считается то, которому соответствует на числовой прямой точка, лежащая левее, и большим считается то, которому соответствует на числовой прямой точка, лежащая правее. Было отмечено, что справедливо следующее утверждение: 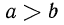 тогда и только тогда, когда
тогда и только тогда, когда  положительное число;
положительное число; 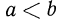 тогда и только тогда, когда
тогда и только тогда, когда  отрицательное число.
отрицательное число.
Если два числа а и b соединить одним из следующих знаков: 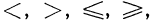 то получится числовое неравенство. Например,
то получится числовое неравенство. Например, 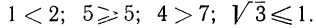 Каждое числовое неравенство есть по существу запись высказывания, например
Каждое числовое неравенство есть по существу запись высказывания, например 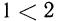 есть запись высказывания «число 1 меньше числа 2» Каждое высказывание может быть истинным или ложным; соответственно, каждое числовое неравенство может быть верным или неверным. Так, из написанных выше четырех числовых неравенств первые два являются верными, а последние два — неверными.
есть запись высказывания «число 1 меньше числа 2» Каждое высказывание может быть истинным или ложным; соответственно, каждое числовое неравенство может быть верным или неверным. Так, из написанных выше четырех числовых неравенств первые два являются верными, а последние два — неверными.
Условимся всюду в дальнейшем, говоря о числовых неравенствах, иметь в виду только верные неравенства, т. е. запись 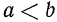 понимать как запись истинного высказывания «число а меньше числа b». Аналогично мы будем понимать записи
понимать как запись истинного высказывания «число а меньше числа b». Аналогично мы будем понимать записи 
Отметим некоторые свойства числовых неравенств:
1°. Если 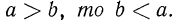
2°. Если 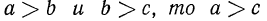 (свойство транзитивности).
(свойство транзитивности).
3°. Если 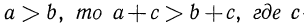 —любое действительное число (свойство монотонности).
—любое действительное число (свойство монотонности).
Эти три свойства легко иллюстрируются на числовой прямой: свойство 1° означает, что если точка а лежит правее точки b, то точка b лежит левее точки а; свойство 2° означает, что если точка а лежит правее b, a b — правее с, то точка а лежит на числовой прямой правее точки с; наконец, геометрическая иллюстрация свойства 3° представлена на рис. 73.
4°. Если 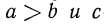 положительное число
положительное число 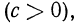 то
то 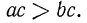
Доказательство:
Рассмотрим разность  Имеем
Имеем 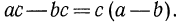 По условию с — положительное число. Далее, так как
По условию с — положительное число. Далее, так как  то разность
то разность  —положительное число. Но произведение двух положительных чисел есть число положительное, значит,
—положительное число. Но произведение двух положительных чисел есть число положительное, значит, 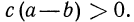 Таким образом,
Таким образом, 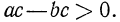 Но если разность
Но если разность  есть число положительное, то
есть число положительное, то 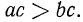 Аналогично доказываются следующие свойства:
Аналогично доказываются следующие свойства:
5°. Если 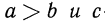 отрицательное число, то
отрицательное число, то 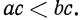
6°. Если 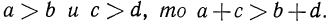
7°. Если а и b — положительные числа и 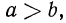 то
то 
Докажите эти свойства самостоятельно.
Замечания:
1. Свойства 1°, 2°, 3° можно доказать таким же методом, каким было доказано свойство 4° (рекомендуем читателю провести соответствующие доказательства).
Свойства 4° и 5° имеют следующий смысл, если обе части верного неравенства умножить на одно и то же положительное число и сохранить знак исходного неравенства, то получится верное неравенство; если обе части верного неравенства умножить на одно и то же отрицательное число и заменить знак неравенства на противоположный, то получится вернее неравенство.
Свойство 6° имеет следующий смысл: если почленно сложить два верных неравенства одного знака и сохранить этот знак неравенства, то получится вернее неравенство.
Остановимся еще на одном свойстве неравенств.
8°. Если а, b, с, d— положительные числа и если 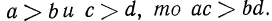
Доказательство:
Имеем 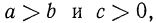 поэтому
поэтому  поэтому
поэтому 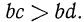 Но из неравенств
Но из неравенств 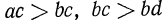 следует по свойству транзитивности неравенство
следует по свойству транзитивности неравенство 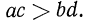
Итак, при почленном умножении верных неравенств одинакового смысла с положительными членами верным будет неравенство того же знака.
Замечание:
Перечисленные выше 8 свойств верны не только для знака 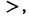 но и для каждого из остальных знаков неравенств
но и для каждого из остальных знаков неравенств 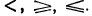
Например, верны такие свойства:
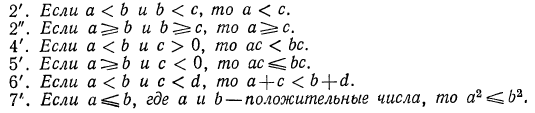
Метод, примененный при доказательстве свойства 4, используется и для доказательства многих неравенств с переменными. Задачу «доказать, что при любых рассматриваемых значениях переменных заданное неравенство с переменными обращается в верное числовое неравенство» мы будем решать следующим образом: составим разность левой и правой частей неравенства и установим, что эта разность при рассматриваемых значениях переменных положительна (или соответственно отрицательна, неположительна, неотрицательна).
Примеры:
1. Доказать, что для любого положительного числа а верно неравенство 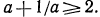
Доказательство:
Составим разность 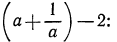
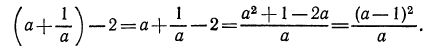
Рассмотрим выражение 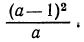 При любом значении а выражение
При любом значении а выражение 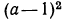 принимает неотрицательное значение. Так как по условию
принимает неотрицательное значение. Так как по условию 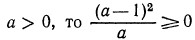 (причем знак равенства имеет место лишь при
(причем знак равенства имеет место лишь при 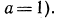
Итак, разность 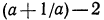 неотрицательна. Это значит, что
неотрицательна. Это значит, что 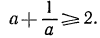
2.Доказать, что если 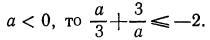
Доказательство:
Составим разность 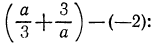
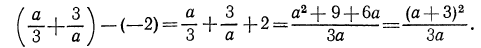
Так как по условию 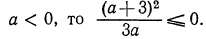 Значит,
Значит, 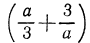
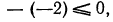
откуда следует требуемое неравенство 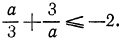
3. Доказать, что если 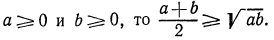
Доказательство:
Имеем:
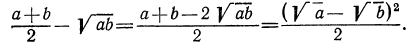
Но 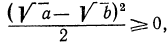 причем равенство достигается лишь в случае
причем равенство достигается лишь в случае  Значит,
Значит, 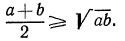
Заметим, что число 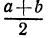 называется средним арифметическим чисел а и b, а число
называется средним арифметическим чисел а и b, а число 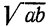 называется средним геометрическим чисел а, Ь. Таким образом, неравенство, доказанное в примере 3, означает, что среднее арифметическое двух неотрицательных чисел всегда больше или равно их среднему геометрическому.
называется средним геометрическим чисел а, Ь. Таким образом, неравенство, доказанное в примере 3, означает, что среднее арифметическое двух неотрицательных чисел всегда больше или равно их среднему геометрическому.
Доказать, что 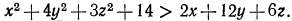
Доказательство:
Рассмотрим разность 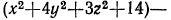
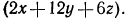
Перегруппировав слагаемые, получим выражение:
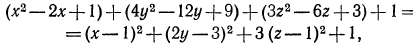
положительное при любых значениях х, у, z. Значит, 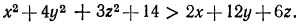
Линейные неравенства
Рассмотрим неравенства вида 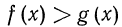 (соответственно
(соответственно 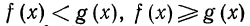
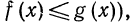 где х—переменная, a
где х—переменная, a 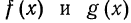 — выражения с переменной х. Если переменной х придать какое-либо числовое значение, то получится числовое неравенство, выражающее либо истинное, либо ложное высказывание. Пусть, например, дано неравенство
— выражения с переменной х. Если переменной х придать какое-либо числовое значение, то получится числовое неравенство, выражающее либо истинное, либо ложное высказывание. Пусть, например, дано неравенство 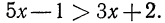 При
При 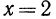 получаем
получаем 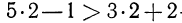 истинное высказывание (верное числовое неравенство); при
истинное высказывание (верное числовое неравенство); при 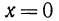 получаем
получаем 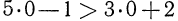 ложное высказывание.
ложное высказывание.
Всякое значение переменной, при котором данное неравенство с переменной обращается в верное числовое неравенство, называется решением неравенства. Решить неравенство с переменной—значит найти множество всех его решений.
Два неравенства с одной переменной х называются равносильными, если множества решений этих неравенств совпадают.
Основная идея решения неравенства состоит в следующем: мы заменяем данное неравенство другим, более простым, но равносильным данному. Такие замены осуществляются на основе следующих утверждений.
1.Если какой-либо член неравенства с переменной перенести из одной части неравенства в другую с противоположным знаком, оставив при этом без изменения знак неравенства, то получится неравенство, равносильное данному.
2.Если обе части неравенства с переменной умножить или разделить на одно и то же положительное число, оставив при этом без изменения знак неравенства, то получится неравенство, равносильное данному.
3.Если обе части неравенства с переменной умножить или разделить на одно и то же отрицательное число, заменив при этом знак неравенства на противоположный, то получится неравенство, равносильное данному.
Ниже на примерах мы покажем применение сформулированных утверждений для решения линейных неравенств, т.е. неравенств вида 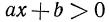 (соответственно
(соответственно 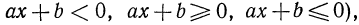 где а и b—действительные числа, и для решения неравенств, сводимых к линейным.
где а и b—действительные числа, и для решения неравенств, сводимых к линейным.
Примеры:
1. Решить неравенство 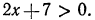
Решение:
Согласно утверждению 1, данному неравенству будет равносильно неравенство 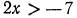 (слагаемое 7 перенесено из одной части неравенства в другую с противоположным знаком, а знак заданного неравенства сставлен без изменения).
(слагаемое 7 перенесено из одной части неравенства в другую с противоположным знаком, а знак заданного неравенства сставлен без изменения).
Разделим обе части неравенства 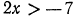 на положительное число 2, а знак неравенства оставим без изменения. Получим неравенство
на положительное число 2, а знак неравенства оставим без изменения. Получим неравенство 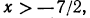 равносильное неравенству
равносильное неравенству 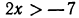 на основании утверждения 2.
на основании утверждения 2.
Итак, неравенство 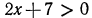 и неравенство
и неравенство 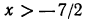 равносильны. Множество решений неравенства
равносильны. Множество решений неравенства  а значит, и заданного неравенства
а значит, и заданного неравенства 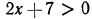 есть промежуток
есть промежуток 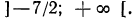
2.Решить неравенство 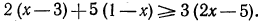
Решение:
Раскрыв скобки, получим:
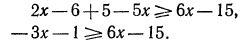
Далее, имеем: 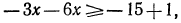 т. е.
т. е.
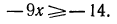
Это неравенство равносильно неравенству (1), а значит, и заданному неравенству согласно утверждению 1.
Разделим теперь обе части неравенства (2) на отрицательное число —9 и изменим знак неравенства. Согласно утверждению 3 получим неравенство, равносильное неравенству (2): 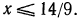 Множество решений последнего неравенства, а вместе с тем и исходного неравенства есть числовой промежуток
Множество решений последнего неравенства, а вместе с тем и исходного неравенства есть числовой промежуток 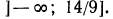
3.Решить неравенство
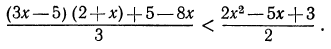
Решение:
Освободимся от знаменателя, для чего умножим обе части неравенства на положительное число 6.
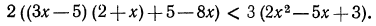
Далее имеем:
Множество решений последнего неравенства, а значит, и равносильного ему заданного неравенства есть промежуток
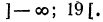
4.Решить неравенство
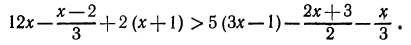
Решение:
Имеем последовательно:
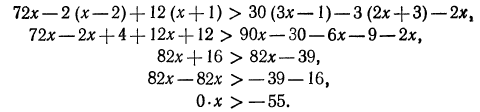
Последнее неравенство верно при любом значении x, так как при любом значении х получится истинное высказывание 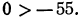 Поэтому множеством его решений (а значит, и множеством решений заданного неравенства) будет вся числовая прямая, т. е. промежуток
Поэтому множеством его решений (а значит, и множеством решений заданного неравенства) будет вся числовая прямая, т. е. промежуток 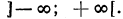
5.Решить неравенство
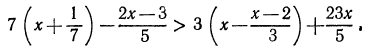
Решение:
Последнее неравенство не имеет решений, так как при любом значении переменной х получается ложнее высказывание  Значит, и заданное неравенство не имеет решений, т. е. множество решений пусто:
Значит, и заданное неравенство не имеет решений, т. е. множество решений пусто: 
Системы и совокупности неравенств
Несколько неравенств с одной переменной образуют систему, если ставится задача найти множество общих решений заданных неравенств. Значение переменной, при котором каждое из неравенств системы обращается в верное числовое неравенство, называется решением системы неравенств. Множество решений системы неравенств есть пересечение множеств решений неравенств, образующих систему.
Неравенства, образующие систему, объединяются фигурной скобкой. Например, запись
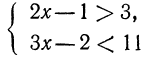
означает, что неравенства 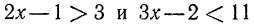 образуют систему.Иногда используется запись в виде двойного неравенства. Например, систему неравенств
образуют систему.Иногда используется запись в виде двойного неравенства. Например, систему неравенств 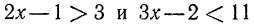 можно записать в виде двойного неравенства
можно записать в виде двойного неравенства 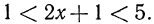
Несколько неравенств с одной переменной образуют совокупность, если ставится задача найти множества всех таких значений переменной, каждое из которых является решением хотя бы одного из данных неравенств. Значение переменной, при котором хотя бы одно из неравенств, образующих совокупность, обращается в верное числовое неравенство, называется решением совокупности неравенств. Множество решений совокупности неравенств есть объединение множеств решений неравенств, образующих совокупность.
Неравенства, образующие совокупность, записываются в строчку и отделяются друг от друга знаком 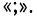
Например, запись
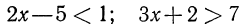
означает, что неравенства образуют совокупность. Иногда для обозначения совокупности неравенств используется квадратная скобка. Так, запись
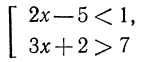
означает, что неравенства образуют совокупность.
Рассмотрим примеры решения систем и совокупностей неравенств.
Примеры:
1. Решить систему неравенств
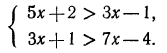
Решение. Первое неравенство системы преобразуется в равносильное ему неравенство  второе — в неравенство
второе — в неравенство 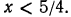
Таким образом, задача сводится к решению системы
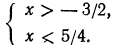
Множество решений неравенства 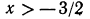 есть промежуток
есть промежуток 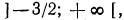 множество решений неравенства
множество решений неравенства 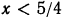 промежуток
промежуток 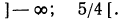 Пересечением этих множеств служит интервал
Пересечением этих множеств служит интервал 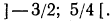 Это и есть множество решений данной системы неравенств (рис. 74).
Это и есть множество решений данной системы неравенств (рис. 74).
2.Решить систему неравенств
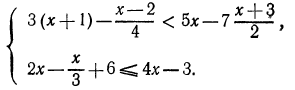
Решение:
Выполнив преобразование каждого из неравенств системы (сделайте это!), получим систему1
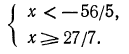
Множество решений неравенства  промежуток
промежуток 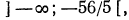 множество решений неравенства
множество решений неравенства 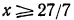 промежуток
промежуток

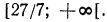 Пересечение этих множеств пусто (рис. 75). Это значит, что заданная система не имеет решений. Ответ:
Пересечение этих множеств пусто (рис. 75). Это значит, что заданная система не имеет решений. Ответ: 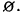
3.Решить систему неравенств
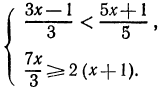
Решение:
После преобразований получим систему
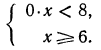
Множеством решений первого неравенства этой системы служит вся числовая прямая, а множеством решений второго неравенства —промежуток 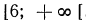 Этот промежуток будет пересечением множеств решений неравенств системы. Ответ:
Этот промежуток будет пересечением множеств решений неравенств системы. Ответ: 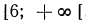
4.Решить систему неравенств
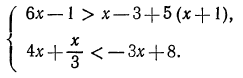
Решение:
После преобразований получим систему
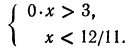
Так как множество решений первого неравенства системы пусто, то и множество решении системы — пустое множество.
Ответ: 
5.Решить совокупность неравенств
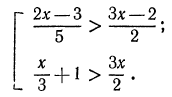
Решение:
Преобразовав каждое из неравенств, получим совокупность 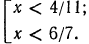 Множество решений неравенства
Множество решений неравенства 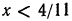 промежуток
промежуток 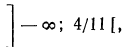 множество решений неравенства
множество решений неравенства 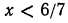 промежуток
промежуток 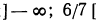 Объединением этих множеств служит промежуток
Объединением этих множеств служит промежуток 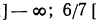 (рис. 76). Это и есть множество решений данной совокупности неравенств.
(рис. 76). Это и есть множество решений данной совокупности неравенств.
Ответ: 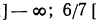
Примеры решения нелинейных неравенств
1.Решить неравенство
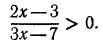
Решение:
Значение дроби положительно тогда и только тогда, когда числитель и знаменатель имеют значения одного знака, т. е. когда
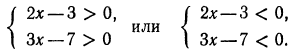
Можно сказать, что заданное неравенство равносильно совокупности двух систем
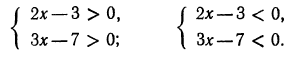
Множество решений первой системы —промежуток 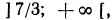 множество решений второй системы —промежуток
множество решений второй системы —промежуток 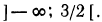 Объединив эти множества, получим множество решений совокупности систем, а вместе с тем и множество решений заданного неравенства.
Объединив эти множества, получим множество решений совокупности систем, а вместе с тем и множество решений заданного неравенства.
Ответ: 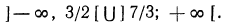
2.Решить неравенство
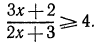
Решение:
Преобразуем заданное неравенство:
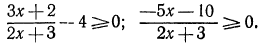
Разделим обе части последнего неравенства на (—5):
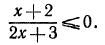
Значение дроби отрицательно в том и только в том случае, когда числитель и знаменатель имеют значения противоположных знаков; дробь обращается в нуль, когда числитель равен нулю, а знаменатель отличен от нуля. Воспользовавшись этим замечанием, приходим к следующей совокупности двух систем:
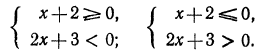
Множество решений первой системы промежуток 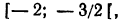 множество решений второй системы пусто. Значит, множество решений совокупности, а поэтому и заданного неравенства — промежуток
множество решений второй системы пусто. Значит, множество решений совокупности, а поэтому и заданного неравенства — промежуток 
3.Решить уравнение 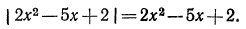
Решение:
Так как 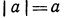 в том и только в том случае, когда
в том и только в том случае, когда 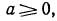 то задача сводится к решению неравенства
то задача сводится к решению неравенства
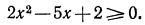
Найдем корни трехчлена 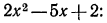
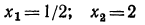
и разложим этот трехчлен на множители, тогда
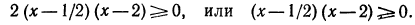
Последнее неравенство равносильно следующей совокупности систем:
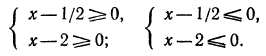
Множество решений первой системы—промежуток 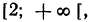 второй—промежуток
второй—промежуток 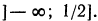 Объединение этих множеств будет множеством решений совокупности систем, а вместе с тем и множеством решений данного уравнения.
Объединение этих множеств будет множеством решений совокупности систем, а вместе с тем и множеством решений данного уравнения.
Ответ: 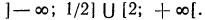
4.Решить неравенство
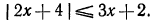
Решение:
Если 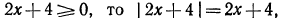 и, следовательно, неравенство (3) примет вид:
и, следовательно, неравенство (3) примет вид:  Если же
Если же 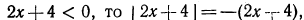 и неравенство (3) принимает вид:
и неравенство (3) принимает вид: 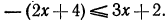 Таким образом, неравенство (3) равносильно следующей совокупности двух систем:
Таким образом, неравенство (3) равносильно следующей совокупности двух систем:
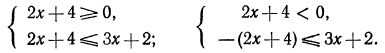
Множество решений первой системы —промежуток 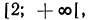 множество решений второй системы пусто. Значит, множеством решений совокупности систем, а тем самым и неравенства (3) служит промежуток
множество решений второй системы пусто. Значит, множеством решений совокупности систем, а тем самым и неравенства (3) служит промежуток 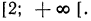
Примеры графического решения неравенств и систем неравенств с одной переменной
1.Решить графически неравенство 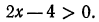
Решение:
Построим график функции 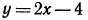 (рис. 77). Мы видим, что график расположен выше оси Ох при значениях х,
(рис. 77). Мы видим, что график расположен выше оси Ох при значениях х,
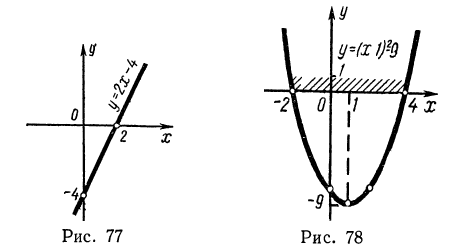
принадлежащих промежутку 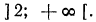 Это и есть множество решений данного неравенства.
Это и есть множество решений данного неравенства.
2.Решить графически неравенство 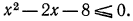
Первый способ решения. Построим график функции 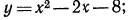 имеем:
имеем:
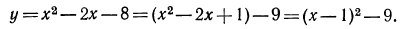
Значит. вершиной параболы 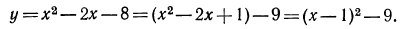 служит точка (1,-9) График изображен на рис.78
служит точка (1,-9) График изображен на рис.78
Мы видим, что график пересекает ось Ох в точках —2 и 4 и расположен ниже оси Ох при значениях принадлежащих интервалу 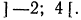 В итоге получаем, что множеством решений заданного неравенства является отрезок
В итоге получаем, что множеством решений заданного неравенства является отрезок 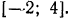
Второй способ. Преобразуем заданное неравенство к виду 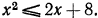 Построим в одной системе координат графики функций
Построим в одной системе координат графики функций 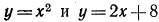 (рис. 79). Неравенство
(рис. 79). Неравенство 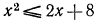 будет выполняться при тех и только тех значениях х, при которых график функции
будет выполняться при тех и только тех значениях х, при которых график функции 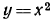 расположен не выше графика функции
расположен не выше графика функции 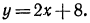
Ответ: [—2: 4].
3.Решить графически систему неравенств
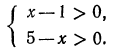
Решение:
Построим в одной системе координат графики функций 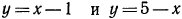 (рис. 80).
(рис. 80).
Оба графика лежат выше оси Ох при значениях х, принадлежащих интервалу 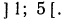 Значит, множество решений заданной системы неравенств есть интервал
Значит, множество решений заданной системы неравенств есть интервал 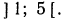
Неравенства — основные понятия и определения
Числовые и алгебраические неравенства. Свойства неравенств. Действия над неравенствами
Поле действительных чисел обладает свойством упорядоченности (п. 6, стр. 35): для любых чисел a, b имеет место одно и только одно из трех соотношений: а > b, а = b, или а < b. При этом запись а > b означает, что разность а—b положительна, а запись а < b — что разность а—b отрицательна. В отличие от поля действительных чисел, поле комплексных чисел не упорядочивается: для комплексных чисел понятия «больше» и «меньше» не определяются; поэтому в данной главе рассматриваются только действительные числа.
Соотношения а > b и а < b назовем неравенствами, числа а и b —членами (или частями) неравенства, знаки 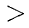 (больше) и
(больше) и 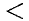 (меньше)—знаками неравенства.
(меньше)—знаками неравенства.
Неравенства а > b и с > d называются неравенствами одинакового (или одного и того же) смысла; неравенства а > b и с < d называются неравенствами противоположного (или разного) смысла.
Из определения неравенства сразу следует, что
1) любое положительное число больше нуля;
2) любое отрицательное число меньше нуля;
3) любое положительное число больше любого отрицательного числа;
4) из двух отрицательных чисел больше то, абсолютная величина которого меньше.
Все эти утверждения допускают простое геометрическое истолкование. Пусть положительное направление числовой оси идет вправо от начальной точки; тогда, каковы бы ни были знаки чисел, большее из них изображается точкой, лежащей правее точки, изображающей меньшее число.
Неравенства обладают следующими основными свойствами.
1 . Несимметричность (необратимость): если а > b, то b < а, и обратно.
Действительно, если разность а—b положительна, то разность b—а отрицательна. Говорят, что при перестановке членов неравенства надо смысл неравенства изменить на противоположный.
2. Транзитивность: если а > b и b > с, то а > с.
Действительно, из положительности разностей а—b и b—с следует и положительность а — с = (а—b) + (b—с).
Кроме знаков неравенства  и
и 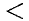 применяют также знаки неравенства
применяют также знаки неравенства  и
и 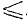 . Они определяются следующим образом: запись
. Они определяются следующим образом: запись  означает, что либо
означает, что либо 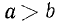 либо
либо 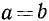 . Поэтому, например, можно писать
. Поэтому, например, можно писать  , а также
, а также 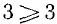 . Обычно неравенства, записанные с помощью знаков
. Обычно неравенства, записанные с помощью знаков 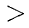 ,
, 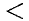 , называют строгими неравенствами, а записанные с помощью знаков
, называют строгими неравенствами, а записанные с помощью знаков 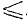 ,
,  — нестрогими неравенствами. Соответственно и сами знаки называют знаками строгого или нестрогого неравенства. Свойства 1 и 2, рассмотренные выше, верны и для нестрогих неравенств.
— нестрогими неравенствами. Соответственно и сами знаки называют знаками строгого или нестрогого неравенства. Свойства 1 и 2, рассмотренные выше, верны и для нестрогих неравенств.
Рассмотрим теперь действия, которые можно производить над одним или несколькими неравенствами.
3. От прибавления к членам неравенства одного и того же числа смысл неравенства не изменяется.
Доказательство:
Пусть даны неравенство а > b и произвольное число m. По определению разность а—b положительна. Прибавим к этому числу два противоположных числа m и (—m), от чего оно не изменится, т. е.
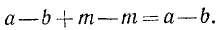
Это равенство можно переписать так:
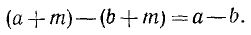
Из этого следует, что разность (a + m)—(b + m) положительна, т. е. что
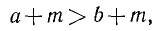
а это и надо было доказать.
На этом основана возможность перекоса любого члена неравенства из одной его части в другую с противоположным знаком. Например, из неравенства
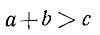
следует, что
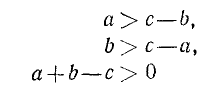
и т. п.
4. При умножении членов неравенства на одно и то же положительное число смысл неравенства не изменяется; при умножении членов неравенства на одно и то же отрицательное число смысл неравенства изменяется на противоположный.
Доказательство:
Пусть а > b; тогда а—b > 0 . Если m > 0, то m(а—b) > 0, так как произведение положительных чисел положительно. Раскрыв скобки в левой части последнего неравенства, получим am—bm > 0, т. е. am > bm. Аналогичным образом рассматривается случай m < 0.
Точно такой же вывод можно сделать и относительно деления частей неравенства на какое-либо отличное от нуля число, так как деление на число 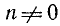 равносильно умножению на число 1/n, а числа n и 1/n имеют одинаковые знаки.
равносильно умножению на число 1/n, а числа n и 1/n имеют одинаковые знаки.
5. Пусть члены неравенства положительны. Тогда при возведении его членов в одну и ту же положительную степень смысл неравенства не изменяется.
Доказательство:
Пусть а > b, b > 0 (в этом случае по свойству транзитивности и а > 0). Тогда в силу монотонного возрастания степенной функции 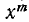 при х > 0 и положительном m будем иметь
при х > 0 и положительном m будем иметь 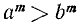 .
.
В частности, если m = 1/k, где k — натуральное число, то получим
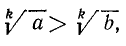
т. е. при извлечении корня из обеих частей неравенства с положительными членами смысл неравенства не изменяется.
Пусть члены неравенства отрицательны. Тогда нетрудно доказать, что при возведении его членов в нечетную натуральную степень смысл неравенства не изменится, а при возведении в четную натуральную степень изменится на противоположный. Из неравенств с отрицательными членами можно также извлекать корень нечетной степени.
Пусть, далее, члены неравенства имеют разные знаки. Тогда при возведении его в нечетную степень смысл неравенства не изменится, а при возведении в четную степень о смысле получающегося неравенства ничего определенного в общем случае сказать нельзя. В самом деле, при возведении числа в нечетную степень знак числа сохраняется и поэтому смысл неравенства не изменяется. При возведении же неравенства в четную степень образуется неравенство с положительными членами, и его смысл будет зависеть от абсолютных величин членов исходного неравенства— может получиться неравенство того же смысла, что и исходное, неравенство противоположного смысла и даже равенство!
6. От неравенства а > b можно перейти к неравенству между 1/а и 1/b: если члены неравенства оба положительны или оба отрицательны, то между их обратными величинами имеется неравенство противоположного смысла: 1/а < 1/b.
Доказательство:
Если а и b—одного знака, то их произведение ab положительно. Разделим на ab неравенство а > b:
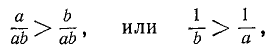
т.е. 1/a < 1/b, что и требовалось получить.
Если члены неравенства имеют противоположные знаки, то неравенство между их обратными величинами имеет тот же смысл, так как знаки обратных величин те же, что и знаки самих величин.
7. Логарифмирование неравенств можно производить лишь в случае, когда члены неравенств положительны (отрицательные числа и нуль логарифмов не имеют).
Пусть b > с, с > 0. Тогда при а > 1 будет
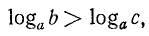
а при 0 < а < 1 будет
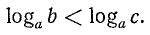
Правильность этих утверждений основана на монотонности логарифмической функции, которая возрастает, если основание а > 1, и убывает при а < 1 (п. 43).
Итак, при логарифмировании неравенства, состоящего из положительных членов, по основанию, большему единицы, образуется неравенство того же смысла, что и данное, а при логарифмировании его по полоокительному основанию, меньшему единицы, — неравенство противоположного смысла.
8. Если b > с и а > 1, то 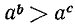 ; если b > c, но 0 < а < 1, то
; если b > c, но 0 < а < 1, то 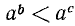 .
.
Это сразу следует из свойств монотонности показательной функции ах (п. 42), которая возрастает в случае а > 1 и убывает, если 0 < а < 1.
9. При почленном сложении неравенств одного и того же смысла образуется неравенство того же смысла, что и данные.
Доказательство:
Докажем это утверждение для двух неравенств, хотя оно верно для любого количества складываемых неравенств. Пусть даны неравенства а > b и с > d. По определению числа а—b и с—d будут положительными; тогда положительной оказывается и их сумма, т. е.
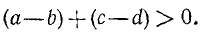
Группируя иначе слагаемые, получим
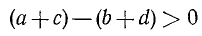
и, следовательно,
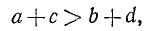
а это и надо было доказать.
Нельзя сказать ничего определенного в общем случае о смысле неравенства, получающегося при сложении двух или нескольких неравенств разного смысла.
10. Если из одного неравенства почленно вычесть другое неравенство противоположного смысла, то образуется неравенство того же смысла, что и первое.
Доказательство:
Пусть даны два неравенства а > b и c > d. Сложим теперь два неравенства а > b и d > с одинакового смысла и получим неравенство
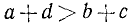
того же смысла. Из последнего находим
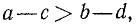
а это и надо было доказать.
Нельзя сказать ничего определенного в общем случае о смысле неравенства, получающегося при вычитании из одного неравенства другого неравенства того же смысла.
11. Если почленно перемножить два неравенства одинакового смысла с положительными членами, то образуется неравенство того же смысла.
Доказательство:
Пусть а > b, с > d, причем b > 0, d > 0. Находим, умножая первое неравенство на с, а второе на b:

откуда в силу транзитивности
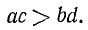
Отсюда снова вытекает правило о возведении неравенства с положительными членами в натуральную степень.
12. Для любого числа а имеет место неравенство 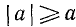 .
.
Доказательство:
Если  , то справедливо равенство |а| = a. Если а < 0, то |а|>0 и имеется строгое неравенство |а|> а. В обоих случаях можно писать
, то справедливо равенство |а| = a. Если а < 0, то |а|>0 и имеется строгое неравенство |а|> а. В обоих случаях можно писать 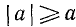 , что и требовалось получить.
, что и требовалось получить.
13. Модуль суммы не превосходит суммы модулей:
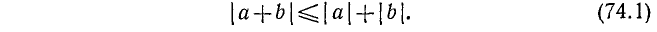
Доказательство:
Модуль суммы |a + b| равен либо а + b, либо —(а + b). По свойству 12 имеем
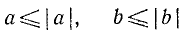
и, складывая эти неравенства почленно (по свойству 9), найдем
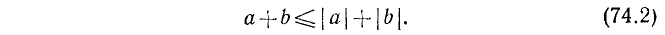
Точно так же 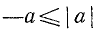 ,
, 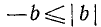 и
и
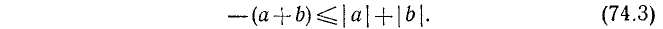
Из неравенств (74.2) и (74.3) видно, что 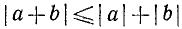 .
.
В действительности нетрудно выяснить, когда имеет место знак равенства и когда знак строгого неравенства: 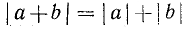 , если а и b одного знака, |а + b| < |а| + |b|, если а и b противоположных знаков.
, если а и b одного знака, |а + b| < |а| + |b|, если а и b противоположных знаков.
Например, |5 + 3| = |5| + | 3|; в то же время |5—3| < |5| + |— 3|. Свойство 13 верно и для любого числа слагаемых. Более того, оно обобщается и на комплексные числа (речь идет, конечно, о неравенствах между модулями комплексных чисел, которые являются действительными числами). Именно, если 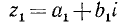 ,
, 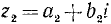 , то
, то 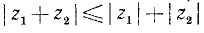 (рекомендуем возвратиться к рис. 9, где сумма комплексных чисел изображена геометрически, и истолковать написанное выше неравенство геометрически).
(рекомендуем возвратиться к рис. 9, где сумма комплексных чисел изображена геометрически, и истолковать написанное выше неравенство геометрически).
14. Разность модулей не больше модуля разности:
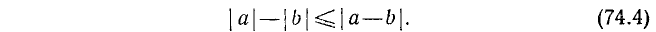
Доказательство:
Запишем очевидное равенство
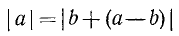
и применим свойство 13:
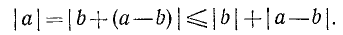
Получим 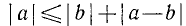 , или
, или 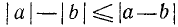 . Неравенство (74.4) допускает следующее усиление:
. Неравенство (74.4) допускает следующее усиление:
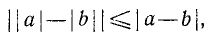
и остается верным и в применении к комплексным числам (доказать самостоятельно).
Алгебраические неравенства
Неравенства между двумя алгебраическими выражениями, такие, например, как
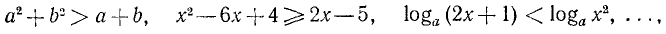
могут при подстановке вместо буквенных параметров, входящих в левую и правую части неравенств, переходить либо в верные, либо в неверные числовые неравенства. Так, неравенство
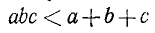
удовлетворяется при а = 1, b = 1 и с = 2 и не удовлетворяется при а = 2, b = 2 и с = 3.
Имеются, однако, такие неравенства, которые оказываются справедливыми для всех допустимых значений входящих в них буквенных параметров. Таковы, например, неравенства (везде мы имеем в виду только действительные значения параметров)
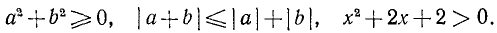
Иногда приходится проводить доказательство неравенств; при этом «доказать неравенство»—значит установить, что оно справедливо для любых допустимых значений параметров.
Пример:
Доказать, что среднее арифметическое двух положительных чисел не меньше их среднего геометрического.
Решение:
Под средним арифметическим двух чисел a > 0 и b > 0 понимают число (а + b)/2, а под их средним геометрическим — число 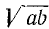 .
.
Требуется доказать справедливость неравенства
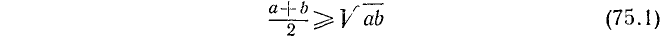
для всех положительных чисел а и b. Данное неравенство равносильно неравенству
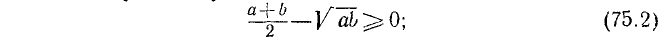
преобразуем левую часть неравенства (75.2):
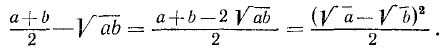
Теперь видно, что неравенство (75.2), а следовательно и неравенство (75.1), выполняется при любых положительных а и b; если  , то неравенство строгое; если же а = b, то среднее арифметическое равно среднему геометрическому.
, то неравенство строгое; если же а = b, то среднее арифметическое равно среднему геометрическому.
Дадим неравенству между средним геометрическим и средним арифметическим также геометрическое истолкование (см. рис. 295, п. 216). Среднее геометрическое двух отрезков а и b, сумма которых принята за диаметр окружности, изображается полухордой MD, а среднее арифметическое— радиусом ОМ, который не меньше этой полухорды.
Неравенство (75.1) также обобщается на случай n положительных чисел  и записывается в форме
и записывается в форме
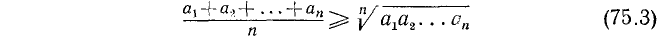
(доказательство мы не приводим).
Пример:
Доказать, что при любом положительном а справедливо неравенство
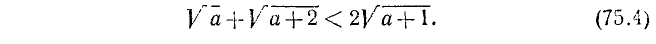
Решение:
Данное неравенство можно записать в равносильной форме:
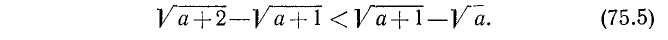
Перенесем иррациональность из числителя в знаменатель:
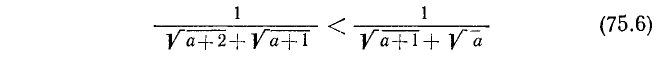
(обе части неравенства преобразуются тождественно). Полученное неравенство верно: числители дробей равны 1, а знаменатель в правой части меньше. Из неравенства (75.6) следует неравенство (75.5), а из него — неравенство (75.4), которое требовалось доказать.
Пример:
Доказать, что во всей области допустимых значений а, b, с имеет место неравенство
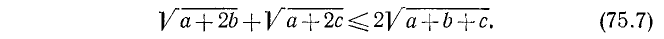
Решение:
Обе части неравенства (75.7) неотрицательны; поэтому мы можем возвести неравенство в квадрат:
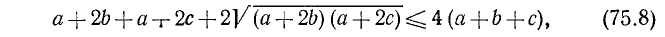
откуда получаем
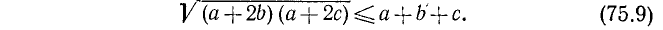
Всякий раз, когда а, b, с лежат в о.д.з. неравенства (75.7) и выполнено неравенство (75.9), будет выполнено и неравенство (75.7). Поэтому доказательство неравенства (75.7) сводится к доказательству неравенства (75.9). Обе его части также неотрицательны. Возводим его в квадрат. Получаем
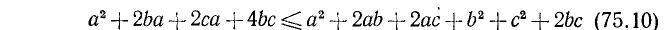
или
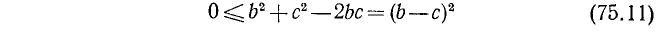
— неравенство, верное при всех значениях а, b, с. В силу неравенства (75.11) устанавливаем последовательно справедливость предшествующих неравенств (75.10), (75.9), (75.8), вплоть до неравенства (75.7), которое требовалось доказать.
Решение неравенств
Множество решений неравенства
Равносильные неравенства. Будем рассматривать строгие или нестрогие неравенства вида
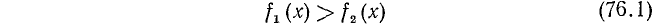
или

соответственно. Всякое числовое значение 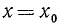 из области допустимых значений называется решением неравенства (76.1) или (76.2), если при подстановке этого значения
из области допустимых значений называется решением неравенства (76.1) или (76.2), если при подстановке этого значения 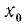 в обе части неравенства получается верное числовое неравенство. Вообще говоря, неравенство может иметь различные решения (часто их бывает бесконечно много). Все решения неравенства образуют множество его решений (иногда называемое также областью его решений). Так, неравенство
в обе части неравенства получается верное числовое неравенство. Вообще говоря, неравенство может иметь различные решения (часто их бывает бесконечно много). Все решения неравенства образуют множество его решений (иногда называемое также областью его решений). Так, неравенство 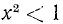 имеет в качестве своего множества решений открытый интервал (—1, 1), — 1 < х < 1, а неравенство
имеет в качестве своего множества решений открытый интервал (—1, 1), — 1 < х < 1, а неравенство 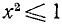 — отрезок [—1, 1],
— отрезок [—1, 1], 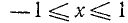 . Иногда, краткости ради, мы допускаем вольность речи и говорим, что решением неравенства
. Иногда, краткости ради, мы допускаем вольность речи и говорим, что решением неравенства 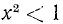 служит интервал (—1, 1); в этом случае слово «решение» имеет смысл «множество решений».
служит интервал (—1, 1); в этом случае слово «решение» имеет смысл «множество решений».
В зависимости от своего конкретного вида неравенство может вообще не иметь решений (его множество решений пусто) или иметь множество решений самого различного вида (открытый интервал, отрезок, бесконечный интервал и т. д.). В любом случае решить неравенство — значит указать все множество его решений. В частности, неравенство может выполняться для всех (допустимых) значений х.
Из двух неравенств
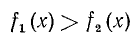
и
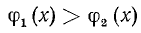
второе называется следствием первого, если множество решений второго неравенства содержит в себе множество решений первого неравенства. Два неравенства называются равносильными, если каждое из них является следствием другого. Иначе это можно сформулировать так: два неравенства считаются равносильными, если их множества решений совпадают. Эти определения аналогичны соответствующим определениям для уравнений (п. 54). Как и для уравнений, можно было бы сформулировать утверждения о действиях, преобразующих данное неравенство в равносильное ему. Такими действиями могут быть прибавление к обеим частям неравенства одинакового слагаемого (и, как следствие, перенос слагаемого с противоположным знаком из одной части неравенства в другую) и умножение обеих частей неравенства на положительное число или положительную функцию. Возможно также деление членов неравенства на положительную функцию и т. д. Следует, однако, производя эти действия, следить, чтобы не изменилась область допустимых значений, так как иначе равносильность неравенств может быть нарушена.
Пример:
Из двух неравенств
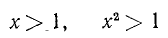
второе является следствием первого, но они не равносильны. Неравенства же 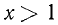 и
и 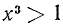 равносильны.
равносильны.
Соблюдение требования равносильности преобразований неравенства, выполняемых в процессе его решения, важней соблюдения соответствующего требования для уравнений. Действительно, можно не опасаться появления посторонних корней при решении уравнений, так как последующая проверка подстановкой в исходное уравнение позволяет их отбросить. Для неравенства характерно наличие бесконечного множества решений, и поэтому проверка их подстановкой в неравенство практически невозможна. По этой же причине и отыскание о.д.з. для решаемого неравенства является необходимой составной частью процесса решения.
Графическое решение неравенств
Если неравенство записано в виде f(х) > 0, то, построив график функции y = f(x), можно непосредственно по чертежу видеть, для каких значений х неравенство удовлетворяется (график лежит выше oси Ох). Решение будет точным или приближенным в зависимссти от того, точно или приближенно найдены точки, где график переходит из нижней полуплоскости у < 0 в верхнюю полуплоскость у > 0.
Если неравенство задано в виде 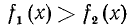 , то можно построить графики двух функций
, то можно построить графики двух функций 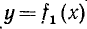 и
и 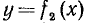 и по чертежу определять, для каких значений х первый график располагается выше второго. Множество таких х и даст множество решений неравенства.
и по чертежу определять, для каких значений х первый график располагается выше второго. Множество таких х и даст множество решений неравенства.
Основная ценность графического подхода к решению неравенств состоит в том, что уже схематическое изображение графиков функций часто показывает, что неравенство выполняется в интервалах, ограниченных такими характерными точками, как точки пересечения графиков 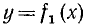 и
и 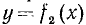 между собой (или точки пересечения графика
между собой (или точки пересечения графика 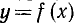 с осью Ох). Отыскание этих точек является уже несколько более легкой задачей: оно сводится к решению уравнений, а ие неравенств.
с осью Ох). Отыскание этих точек является уже несколько более легкой задачей: оно сводится к решению уравнений, а ие неравенств.
Пример:
Решить неравенство
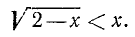
Решение:
Строим графики функций 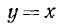 и
и 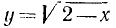 (рис. 62). Первый из них нам известен, второй представляет собой часть параболы
(рис. 62). Первый из них нам известен, второй представляет собой часть параболы 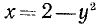 лежащую в верхней полуплоскости. Из чертежа видно, что неравенство удовлетворяется в интервале (а, 2), левый конец которого —корень уравнения
лежащую в верхней полуплоскости. Из чертежа видно, что неравенство удовлетворяется в интервале (а, 2), левый конец которого —корень уравнения 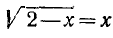 . Решаем это уравнение:
. Решаем это уравнение:  ,
, 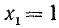 ,
,  .
.
Корень 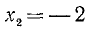 — посторонний, нужное нам значение:
— посторонний, нужное нам значение: 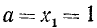 . Итак, неравенство удовлетворяется в интервале (1, 2).
. Итак, неравенство удовлетворяется в интервале (1, 2).
Пример:
Решить неравенство
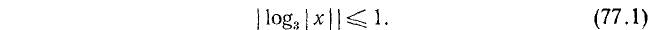
Решение:
Строим график функции 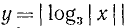 ; на рис.63 пунктиром показан график функции
; на рис.63 пунктиром показан график функции 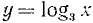 , после чего график
, после чего график 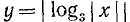 получен по способу п. 48 (он показан сплошной линией). Далее проведена прямая y = 1. Сразу видно, что неравенству (77.1) будут удовлетворять значения х из двух симметричных интервалов: (—b, —а) и (а, b). Здесь через ±а, ±b обозначены абсциссы точек пересечения прямой у = 1 с графиком функции, т. е. решения уравнения
получен по способу п. 48 (он показан сплошной линией). Далее проведена прямая y = 1. Сразу видно, что неравенству (77.1) будут удовлетворять значения х из двух симметричных интервалов: (—b, —а) и (а, b). Здесь через ±а, ±b обозначены абсциссы точек пересечения прямой у = 1 с графиком функции, т. е. решения уравнения
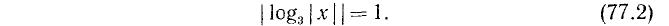
В силу симметрии достаточно найти решения уравнения (77.2) при х > 0. Поэтому уравнение (77.2) сводится к
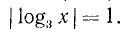
При х > 1 имеем  и из
и из 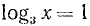 находим х = 3.
находим х = 3.
При х< 1 имеем 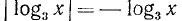 и из
и из 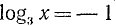 находим x = 1/3. Ясно, что а = 1/3, b = 3 и множеством решений данного неравенства служит пара симметричных интервалов (—3, —1/3) и (1/3, 3).
находим x = 1/3. Ясно, что а = 1/3, b = 3 и множеством решений данного неравенства служит пара симметричных интервалов (—3, —1/3) и (1/3, 3).
Линейные неравенства. Системы линейных неравенств
Неравенства вида
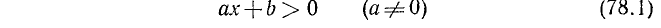
(а также 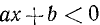 ,
, 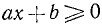 ,
, 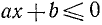 называются линейными неравенствами или неравенствами первой степени.
называются линейными неравенствами или неравенствами первой степени.
Для решения неравенства (78.1) перенесем свободный член в правую часть неравенства с противоположным знаком:

Приходится различать два случая: а > 0 и а < 0. Если а > 0, то разделим обе части неравенства (78.2) на а и получим равносильное неравенство х > —b/а, которое показывает, что множество решений неравенства (78.1) в данном случае — бесконечный интервал 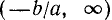 . Если a < 0, то при делении обеих частей неравенства (78.2) на а придется изменить смысл неравенства, х < —b/а, и решением неравенства (78.1) в этом случае будет бесконечный интервал
. Если a < 0, то при делении обеих частей неравенства (78.2) на а придется изменить смысл неравенства, х < —b/а, и решением неравенства (78.1) в этом случае будет бесконечный интервал 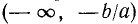 .
.
Замечание:
Если бы а = 0, то неравенство (78.1) не содержало бы х и было бы либо верным, либо неверным числовым неравенством.
Пример:
Решить неравенства: а) Зх + 4 > х + 10; б) 6х+ 1 >10х + 3.
Решение:
а) Перенесем члены, содержащие х, в левую часть неравенства, а свободные члены — в правую часть:
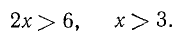
Решением неравенства является интервал 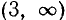 .
.
б) Перенесем неизвестные члены в левую часть, а известные — в правую часть неравенства:
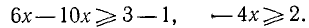
При делении неравенства на отрицательное число (—4) изменим смысл неравенства на противоположный, получим 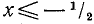 .
.
Множеством решений данного неравенства служит бесконечный интервал 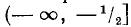 .
.
Пример:
Решить (и исследовать) неравенство
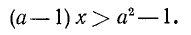
Решение:
Различаем случаи:
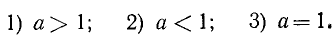
При а > 1 делим обе части на а—1 и сохраняем смысл неравенства: х > а + 1. При а < 1 одновременно с делением на а—1 изменяем смысл неравенства: х < а + 1. При а = 1 неравенство не выполняется ни при каком х.
Ответ. Если а > 1, то множеством решений служит интервал 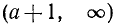 ; если a < 1, то множество решений — интервал
; если a < 1, то множество решений — интервал 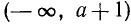 ; при а = 1 решений не имеется.
; при а = 1 решений не имеется.
В случае, если задана система линейных неравенств с одной неизвестной х, например система двух неравенств вида
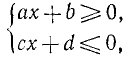
то ее решение проводится так: решают каждое неравенство в отдельности, а затем находят те значения х, которые входят во множества решений каждого из неравенств. В случае двух неравенств решением каждого из них служит бесконечный интервал вида 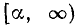 или
или 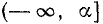 . Можно представить себе четыре основные возможности, поясняемые рис. 64, где I и II обозначают области решений первого и второго неравенств.
. Можно представить себе четыре основные возможности, поясняемые рис. 64, где I и II обозначают области решений первого и второго неравенств.
1) Решениями обоих неравенств служат бесконечные интервалы вида 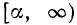 ,
, 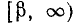 соответственно, т. е. лучи положительного направления с начальными точками
соответственно, т. е. лучи положительного направления с начальными точками 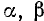 . Если, например,
. Если, например,  , то решением системы неравенств будет общая часть этих лучей — луч
, то решением системы неравенств будет общая часть этих лучей — луч  . Этот случай показан на рис. 64, а.
. Этот случай показан на рис. 64, а.
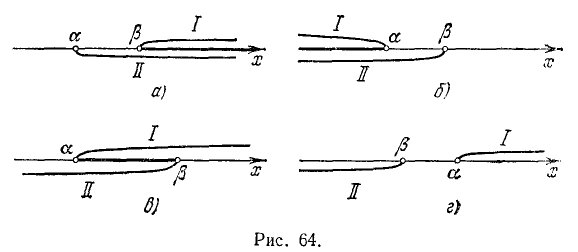
2) Решения неравенств — бесконечные интервалы (лучи) вида  ,
, 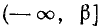 . Решением системы служит тот из этих интервалов, который содержится в другом; при
. Решением системы служит тот из этих интервалов, который содержится в другом; при 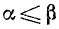 таким является интервал
таким является интервал 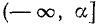 (рис. 64, б).
(рис. 64, б).
3) Решение одного из неравенств — луч 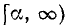 , другого — луч
, другого — луч 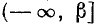 , причем
, причем  (рис. 64, в). Общей частью бесконечных интервалов, представляющих решения неравенств системы при
(рис. 64, в). Общей частью бесконечных интервалов, представляющих решения неравенств системы при 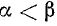 , является сегмент
, является сегмент 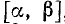 , который и служит множеством решений системы. При
, который и служит множеством решений системы. При 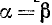 множество решении сведется к одной точке
множество решении сведется к одной точке 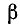 .
.
4) Решения неравенств — лучи 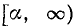 и
и 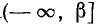 , причем
, причем  (рис. 64, г). В этом случае ни одна точка числовой оси не удовлетворяет обоим неравенствам одновременно. Система неравенств не имеет решений (множество ее решений пусто).
(рис. 64, г). В этом случае ни одна точка числовой оси не удовлетворяет обоим неравенствам одновременно. Система неравенств не имеет решений (множество ее решений пусто).
Пример:
Решить системы неравенств:
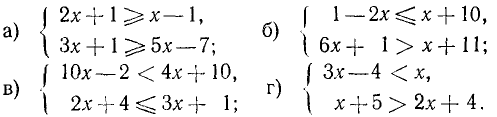
Решение:
а) Решим равенства системы:
Обоим неравенствам одновременно удовлетворяют все числа, большие или равные (—2), но меньшие или равные 4. Записать решение данной системы поэтому можно так: 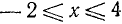 . Не множество решений — сегмент
. Не множество решений — сегмент 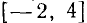 .
.
При отыскании множества решений системы полезно пользоваться наглядным приемом, который в данном случае проводится так: интервал, содержащий решения одного неравенства, покрывается штриховкой в одном направлении (на рис. 65, а
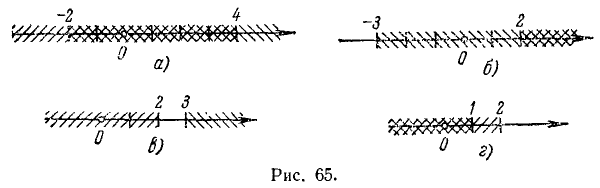
в направлении слева вниз направо), а интервал, содержащий решения другого неравенства, — в другом направлении (на рис. 65, а слева вверх направо). Множеством решений системы будет служить дважды заштрихованный интервал числовой оси.
б) Множеством решений первого неравенства служит интервал 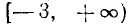 , а второго — интервал
, а второго — интервал 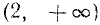 . Следовательно, множества решений системы — бесконечный интервал
. Следовательно, множества решений системы — бесконечный интервал 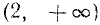 ; на рис. 65, б это отчетливо видно.
; на рис. 65, б это отчетливо видно.
в) Первому неравенству удовлетворяют все числа, меньшие 2, а второму—все числа, большие или равные 3. Множества решений неравенств, составляющих систему, общих точек не имеют (рис. 65, в). Неравенства несовместны, система противоречива.
г) Множеством решений первого неравенства служит интервал 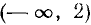 , а второго — интервал
, а второго — интервал 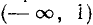 . Поэтому множеством решений системы является бесконечный интервал
. Поэтому множеством решений системы является бесконечный интервал 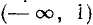 ; это видно из рис. 65, г.
; это видно из рис. 65, г.
К системам неравенств приводят неравенства, содержащие неизвестную под знаком абсолютной величины. Ограничимся решением типичного примера.
Пример:
Решить неравенство
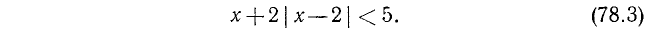
Решение:
Для того чтобы записать неравенство без знака модуля, придется рассмотреть две возможности: 1)  и 2)
и 2) 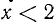 .
.
1)  ; тогда неравенство (78.3) принимает вид Зх — 4 < 5 и мы приходим к системе неравенств
; тогда неравенство (78.3) принимает вид Зх — 4 < 5 и мы приходим к системе неравенств
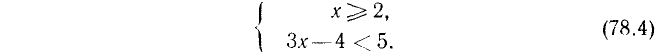
2) х < 2; в этом случае неравенство (78.3) сводится к виду — х + 4 < 5 и получается система
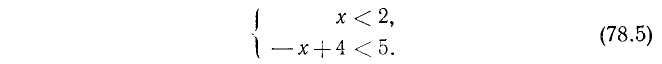
Множество решений неравенства (78.3) будет объединением множеств решений систем (78.4) и (78.5). Первая система имеет своим решением интервал [2, 3), вторая — интервал (—1, 2). Итак, решение неравенства (78.3) — интервал (—1, 3).
Квадратные неравенства
Квадратным неравенством или неравенством второй степени называется неравенство вида
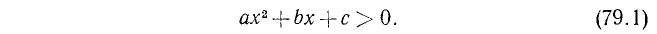
Так как исследование знака квадратного трехчлена по существу полностью проведено в п. 45 в связи с построением графика этой функции и наглядно представлено на рис. 45, то можно здесь воспользоваться этими результатами. В зависимости от знаков дискриминанта 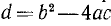 и старшего коэффициента а представляются следующие возможности:
и старшего коэффициента а представляются следующие возможности:
1) d < 0, а > 0. Неравенство (79.1) выполнено при всех значениях а (трехчлен положителен для всех значений аргумента). Этот случай представлен рис. 45, а (см. стр. 132).
2) d < 0, а < 0. Неравенство не выполняется ни для одного значения х, множество его решений пусто (рис. 45, б).
3) d = 0, а > 0. Такой трехчлен изображен на рис. 45, д; неравенство (79.1) выполняется для всех х, кроме х = — b/(2а) (двойной корень трехчлена).
4) d = 0, а < 0. Неравенство не может выполняться ни при одном значении х (трехчлен отрицателен всюду, кроме единственной точки х = — b/(2а) , где он обращается в нуль; рис. 45, е).
5) d > 0, а > 0. График трехчлена изображен на рис. 45, в. Неравенство (79.1) выполняется всюду вне интервала между корнями. Если 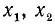 — корни трехчлена, причем
— корни трехчлена, причем 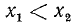 , то неравенство (79.1) выполняется в бесконечных интервалах
, то неравенство (79.1) выполняется в бесконечных интервалах 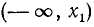 и
и 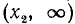 .
.
6) d >0, а < 0. График показан на рис. 45, г; неравенство удовлетворено в интервале между корнями трехчлена (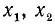 ).
).
В сжатой форме эти положения о знаке квадратного трехчлена формулируют так: квадратный трехчлен с мнимыми корнями имеет постоянный знак, совпадающий со знаком его старшего коэффициента; квадратный трехчлен с различными действительными корнями имеет в интервале между корнями знак, противоположный знаку его старшего коэффициента, а вне интервала между корнями — знак, совпадающий со знаком старшего коэффициента.
Эти результаты для трехчлена с действительными корнями 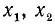 (
(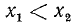 ) можно подкрепить следующими типичными рассуждениями, которые окажутся далее (в п. 80) полезными при решении неравенств высших степеней и неравенств, содержащих дробные рациональные функции. Запишем разложение квадратного трехчлена на множители (п. 60):
) можно подкрепить следующими типичными рассуждениями, которые окажутся далее (в п. 80) полезными при решении неравенств высших степеней и неравенств, содержащих дробные рациональные функции. Запишем разложение квадратного трехчлена на множители (п. 60):
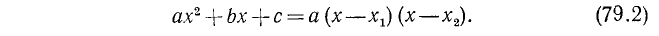
Очевидно, что в областях 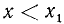 ,
, 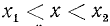 ,
, 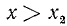 трехчлен имеет определенный знак, одинаковый для каждой точки данной области. При переходе же из области в область, т. е. при переходе х через одно из значений
трехчлен имеет определенный знак, одинаковый для каждой точки данной области. При переходе же из области в область, т. е. при переходе х через одно из значений  , знак его изменяется. Теперь достаточно установить знак трехчлена для каждой из трех указанных областей.
, знак его изменяется. Теперь достаточно установить знак трехчлена для каждой из трех указанных областей.
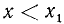 . Имеем
. Имеем 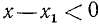 ,
, 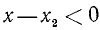 ; знак трехчлена совпадает со знаком а.
; знак трехчлена совпадает со знаком а.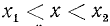 ; в этом случае
; в этом случае 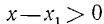 ,
, 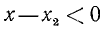 ; знак трехчлена противоположен знаку а.
; знак трехчлена противоположен знаку а.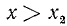 . Теперь уже
. Теперь уже 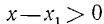 ,
, 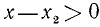 , и знак трехчлена снова совпадает со знаком а.
, и знак трехчлена снова совпадает со знаком а.
Выводы графического и алгебраического исследования полностью совпали.
Пример:
Решить следующие неравенства:
а) 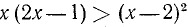 ; б)
; б) 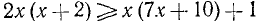 .
.
Решение:
а) Преобразуем данное неравенство:
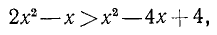
или
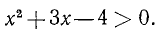
Получилось квадратное неравенство, равносильное данному. Замечаем, что дискриминант трехчлена 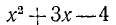 больше нуля и что его корнями служат числа (—4) и 1. Таким образом,
больше нуля и что его корнями служат числа (—4) и 1. Таким образом, 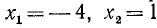 . Множество решений данного неравенства состоит из двух бесконечных интервалов:
. Множество решений данного неравенства состоит из двух бесконечных интервалов: 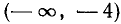 ,
, 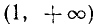 . Этот ответ рекомендуется проверить, построив график трехчлена
. Этот ответ рекомендуется проверить, построив график трехчлена 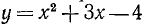 .
.
б) После простых преобразований получаем квадратное неравенство
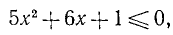
равносильное данному. Дискриминант трехчлена 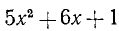 положителен, корнями трехчлена являются числа
положителен, корнями трехчлена являются числа 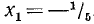 ,
, 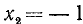 .
.
Множество решений задается неравенствами 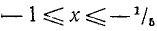 ; они представляют собой сегмент
; они представляют собой сегмент 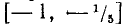 .
.
Пример:
Решить неравенство
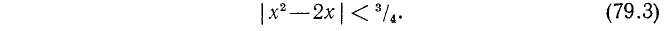
Решение:
Числа, модуль которых меньше а, заполняют интервал от —а до а. Поэтому неравенство (79.3) равносильно следующим неравенствам:
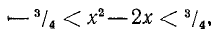
которые составят систему неравенств второй степени для х:
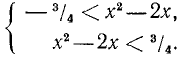
Перепишем их в стандартной форме:
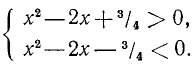
Первое неравенство имеет множество решений 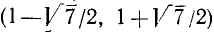 . Решения второго неравенства заполняют два бесконечных интервала:
. Решения второго неравенства заполняют два бесконечных интервала:  и
и  . Методом штриховки нетрудно убедиться, что множество решений данного неравенства состоит из двух интервалов:
. Методом штриховки нетрудно убедиться, что множество решений данного неравенства состоит из двух интервалов: 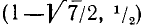 и
и 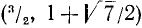 .
.
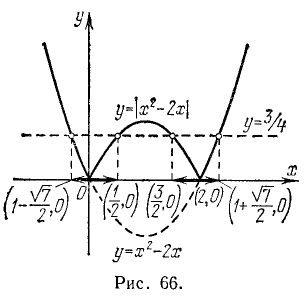
На рис. 66 показана графическая иллюстрация к данному неравенству. 80. Неравенства высших степеней. Неравенства, содержащие дробные рациональные функции от х. Рассмотрим теперь неравенства вида
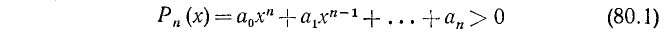
или вида
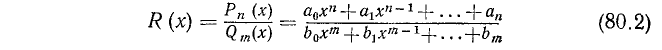
(в левой части этих неравенств помещается, соответственно, целая или дробная рациональная функция от х (п. 50)). Такие неравенства решают путем разложения входящих в них многочленов на множители, после чего оказывается достаточным установить знак левой части неравенства в каждом из интервалов, на которые числовая ось разбивается действительными корнями функции 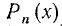 (корнями числителя и знаменателя дробной функции
(корнями числителя и знаменателя дробной функции 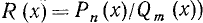 .
.
Пример:
Решить неравенства: а) 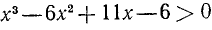 ; б)
; б) 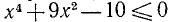 ; в)
; в) 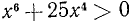 .
.
Решение:
а) Для разложения кубического многочлена на множители найдем его корни. Легко заметить, что делитель 1 свободного члена является одним из корней многочлена (см. п. 62); другие корни равны 2 и 3, так что неравенство запишется в виде
(x — 1)(х — 2) (х — 3) > 0.
Теперь видно, что для х < 1 все три множителя отрицательны, произведение отрицательно. При 1 < х < 2 первый множитель положителен, два других отрицательны. Продолжая такие же рассуждения, найдем, что многочлен положителен в интервалах (1, 2), (3, + ) и отрицателен в интервалах (—
) и отрицателен в интервалах (— , 1), (2, 3). Множество решений неравенства состоит из интервалов (1, 2), (3, +
, 1), (2, 3). Множество решений неравенства состоит из интервалов (1, 2), (3, + ).
).
б) Для разложения левой части неравенства на множители находим ее корни; имеем биквадратное уравнение (п. 64)
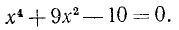
Находим 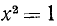 и
и 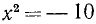 . Запишем разложение левой части неравенства на множители:
. Запишем разложение левой части неравенства на множители:
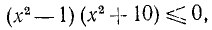
или
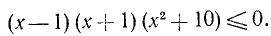
Так как 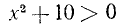 при любых х, то неравенство заменяется равносильным:
при любых х, то неравенство заменяется равносильным:
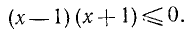
Множеством его решений служит сегмент [—1, 1].
в) Неравенство удовлетворяется при всех значениях 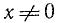 ; множество его решений состоит из интервалов (—
; множество его решений состоит из интервалов (— , 0) и (0,
, 0) и (0,  ).
).
Сходным образом решаются и дробные неравенства.
Пример:
Решить неравенство 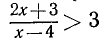 .
.
Решение:
Начнем с предостережения: не следует делать «очевидного» упрощения, состоящего в том, чтобы умножить неравенство на знаменатель х—4 дроби; знаменатель может быть как положительным, так и отрицательным, и в зависимости от его знака при умножении придется рaссматривать два случая.
Вместо этого перенесем все члены неравенства в одну часть. получаем
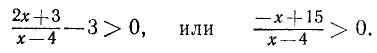
Удобно изменить знак в числителе, одновременно изменив и знак неравенства:
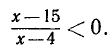
В интервале х < 4 левая часть положительна, в интервале 4 < х < 15 —отрицательна, в интервале х > 15 — вновь положительна. Область решений — интервал (4, 15).
Пример:
Найти все значения х, для которых
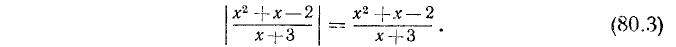
Решение:
Из определения модуля (п. 6) следует, что равенство (80.3) равносильно неравенству
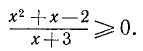
Запишем его в виде
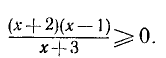
Неотрицательные значения левая часть неравенства принимает в интервалах (—3, —2J и [1, + ). Точки х = — 2 и х = 1 входят в области решений. В них левая часть неравенства обращается в нуль, а это допускается знаком нестрогого неравенства.
). Точки х = — 2 и х = 1 входят в области решений. В них левая часть неравенства обращается в нуль, а это допускается знаком нестрогого неравенства.
Пример:
При каких значениях а корни квадратного уравнения
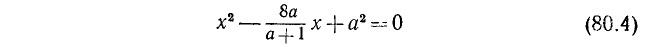
действительные положительные?
Решение:
Корни трехчлена будут действительными при условии, что его дискриминант неотрицателен:
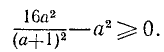
Так как произведение корней по теореме Внета равно 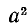 , то при положительных корнях должно быть
, то при положительных корнях должно быть 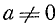 . В то же время из равенства
. В то же время из равенства 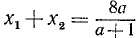 ясно, что корни будут положительными при выполнении условия
ясно, что корни будут положительными при выполнении условия
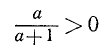
(так как 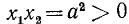 , то знаки корней одинаковы и совпадают со знаком
, то знаки корней одинаковы и совпадают со знаком 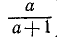 ).
).
Итак, решение примера 4 свелось к решению системы неравенств
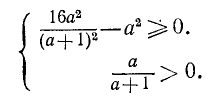
Второе неравенство имеет множество решений, состоящее из интервалов (—  , —1) и (0,
, —1) и (0,  ). Первое неравенство перепишем в виде
). Первое неравенство перепишем в виде
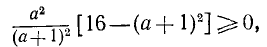
и так как у нас 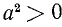 ,
, 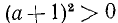 (точки а = 0 и а = —1 не входят уже во множество решений второго неравенства системы), то останется решить неравенство
(точки а = 0 и а = —1 не входят уже во множество решений второго неравенства системы), то останется решить неравенство
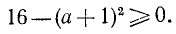
Множеством его решений служит замкнутый интервал [—5, 3]. Точки, одновременно удовлетворяющие обоим неравенствам системы, заполняют интервалы [—5, —1) и (0, 3]. Корни данного уравнения (80.4) действительны и положительны, если
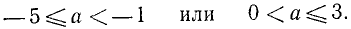
Иррациональные, показательные и логарифмические неравенства
Неравенства, в левые и правые части которых входят алгебраические иррациональности, показательные или логарифмические выражения, содержащие неизвестную, называют, соответственно, иррациональными, показательными и логарифмическими неравенствами. Решение таких неравенств может требовать выполнения действий возведения в степень, потенцирования, логарифмирования. При проведении преобразований, связанных с этими действиями, необходимо учитывать соответствующие правила, относящиеся к неравенствам (п. 74). Приведем типичные примеры на решение неравенств названных типов.
Пример:
Решить неравенство
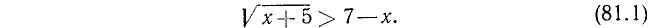
Решение:
Сначала отметим, что о.д.з. задается условием 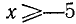 . Далее рассматриваем два возможных случая: 1) правая часть неравенства отрицательна, 2) правая часть неравенства неотрицательна. Если
. Далее рассматриваем два возможных случая: 1) правая часть неравенства отрицательна, 2) правая часть неравенства неотрицательна. Если 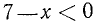 ,
, 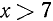 , то неравенство заведомо удовлетворяется: его левая часть не меньше нуля, как арифметическое значение квадратного корня. Остается рассмотреть случай
, то неравенство заведомо удовлетворяется: его левая часть не меньше нуля, как арифметическое значение квадратного корня. Остается рассмотреть случай 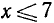 . В этом случае обе части неравенства неотрицательны и неравенство можно, не изменяя его смысла, возвести в квадрат. Получаем
. В этом случае обе части неравенства неотрицательны и неравенство можно, не изменяя его смысла, возвести в квадрат. Получаем
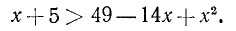
Это приводит к квадратному неравенству
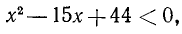
которое удовлетворяется при 4 < х < 11. Но по предположению х < 7; поэтому имеем 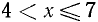 .
.
Итак, неравенство (81.1) удовлетворяется при х > 7 и при 4 < х < 7, т. е., вообще, при х > 4. Множество решений неравенства — луч (4,  ).
).
Пример:
Решить неравенство
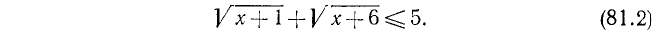
Решение:
В данном случае о.д.з. определяется условие 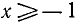 . Так как при любых допустимых значениях х обе части неравенства положительны, то возводим неравенство в квадрат:
. Так как при любых допустимых значениях х обе части неравенства положительны, то возводим неравенство в квадрат:
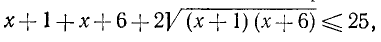
или
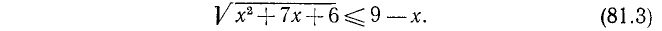
Так как слева имеем неотрицательное выражение, то должно выполняться условие  ; в этом случае можно еще раз возвести в квадрат обе части нового неравенства (81.3) и получить
; в этом случае можно еще раз возвести в квадрат обе части нового неравенства (81.3) и получить
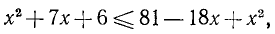
откуда
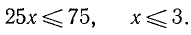
Учитывая все найденные ограничения на х:
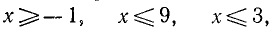
приходим к следующему решению: неравенство (81.2) удовлетворяется для х, лежащих в сегменте [—1, 3].
Пример:
Решить неравенство
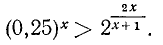
Решение:
Естественно отнести это неравенство к показательным неравенствам. После небольших преобразований запишем неравенство в форме
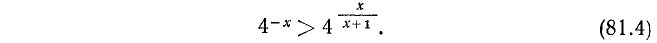
Теперь основания равны 4 > 1 и неравенство между степенями влечет за собой неравенство того же смысла между показателями степени:
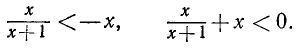
Решаем полученное алгебраическое неравенство обычным способом (метод интервалов):
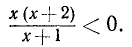
Имеем интервалы

Неравенству (81.4) удовлетворяют точки интервалов (— ,—2) и (-1, 0).
,—2) и (-1, 0).
Пример:
Решить логарифмические неравенства: a) 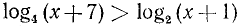 ; б)
; б) 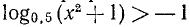 .
.
Решение:
а) Приведем логарифмы, входящие в данное неравенство, к общему основанию, например к основанию 4. Имеем
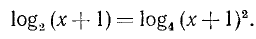
Теперь можно данное неравенство переписать так:
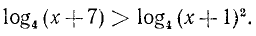
Основание больше единицы. По этой причине логарифмируемые выражения должны быть связаны неравенством того же смысла, что сами логарифмы. Таким образом,
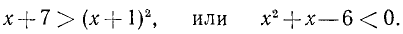
Решим это квадратное неравенство и учтем условие х > — 1, определяющее о.д.з. Получим —1 < х < 2.
Множество решений данного неравенства представляет собой интервал (—1, 2).
б) Заметим, что 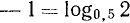 , после чего перепишем данное неравенство так:
, после чего перепишем данное неравенство так: 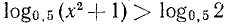 .
.
Отсюда 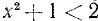 . Это неравенство и данное—разного смысла, поскольку основание 0,5 логарифмов меньше единицы. Решив последнее неравенство, находим, что его решения заполняют конечный интервал (—1, 1).
. Это неравенство и данное—разного смысла, поскольку основание 0,5 логарифмов меньше единицы. Решив последнее неравенство, находим, что его решения заполняют конечный интервал (—1, 1).
Пример:
Решить неравенство
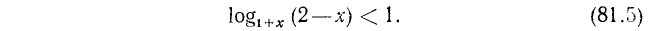
Решение:
В данном примере неизвестная входит как в основание, так и под знак логарифма; заранее неизвестно, будет ли основание логарифма 1 + х больше или меньше единицы, при решении придется учитывать обе эти возможности. Начнем решение примера с указания о.д.з. Ясно, что должно быть — 1< x < 2 и, кроме того,  (гак как основание логарифма не может быть равно 1). Таким образом о.д.з. состоит из интервалов (— 1, 0) и (0, 2). Теперь перепишем неравенство в виде
(гак как основание логарифма не может быть равно 1). Таким образом о.д.з. состоит из интервалов (— 1, 0) и (0, 2). Теперь перепишем неравенство в виде
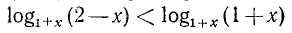
и рассмотрим два случая.
1) —1 < х < 0. В этом случае основание логарифмов меньше единицы, и, потенцируя, мы изменим смысл неравенства на противоположный:
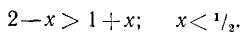
Учитывая все ограничения на х, получаем —1 < х < 0.
2) 0 < х < 2. Теперь основание логарифмов больше единицы, при потенцировании смысл неравенства сохраняется:
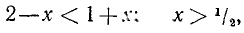
и с учетом о.д.з. имеем 1/2 < x < 2.
Итак, множество решений неравенства (81.5) состоит из интервалов (— 1, 0) и (1/2, 2).
Неравенства с двумя неизвестными
Неравенство с двумя неизвестными
имеет своими решениями пары чисел (х, у), которые изображаются точками плоскости. Найти множество всех решений данного неравенства (или, в других случаях, системы неравенств) — это значит указать на плоскости множество точек, в которых это неравенство (система неравенств) удовлетворяется. Такая необходимость возникает, например, при отыскании о.д.з. алгебраического выражения, зависящего от двух буквенных величин.
Пример:
Указать на плоскости множество решений неравенства: а) х(х—у) > 0; б) 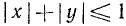 .
.
Решение:
а) Неравенство удовлетворяется в двух случаях: 1) при х > 0, х > y; 2) при х < 0, х < 0.
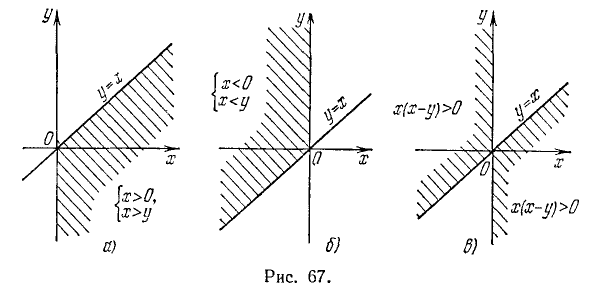
В случае 1) получается часть правой полуплоскости х > 0, лежащая ниже прямой у = х (рис. 67, а). Случаю 2) отвечает часть левой полуплоскости, лежащая выше прямой у = х (рис.67, б). Все множество решений неравенства показано на рис. 57, в.
Линии х = 0 и у = x, ограничивающие заштрихованную область, в нее не входят (так как решалось строгое неравенство).
б) Пусть сначала  ,
, 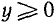 . Тогда получается система неравенств
. Тогда получается система неравенств
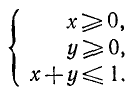
Так как х + у = 1 — уравнение прямой, отсекающей на осях координат отрезки, равные единице, то неравенствам будут
удовлетворять точки треугольника, ограниченного отрезками осей координат и прямой х + у = 1 (в первой четверти; рис. 68, а).
Части области, расположенные в других четвертях, будут симметричны указанному треугольнику (рис. 68, б). В этом легко убедиться, если заметить, что вместе с точкой (х, у) неравенству будут удовлетворять и симметрично расположенные точки (—х, у), (х, —у), (—х, —у). Линии, ограничивающие область, в данном случае ей принадлежат (вследствие того, что неравенство нестрогое).
Пример:
На плоскости Оху показать области, в которых функция
положительна или отрицательна.
Решение:
На плоскости Оху изобразим параболы 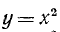 и
и  , отделяющие друг от друга области
, отделяющие друг от друга области 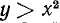 и
и 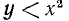 (рис. 69, а), а также области
(рис. 69, а), а также области  и
и 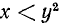 (рис. 69, б). Области, где указанные выражения положительны, заштрихованы (разной штриховкой на рис. 69, а и 69, б). Оба чертежа совмещены на рис. 69, в и теперь видно, что области, покрытые двойной штриховкой и совсем незаштриховаиные, являются областями положительности функции, а однократно заштрихованные
(рис. 69, б). Области, где указанные выражения положительны, заштрихованы (разной штриховкой на рис. 69, а и 69, б). Оба чертежа совмещены на рис. 69, в и теперь видно, что области, покрытые двойной штриховкой и совсем незаштриховаиные, являются областями положительности функции, а однократно заштрихованные
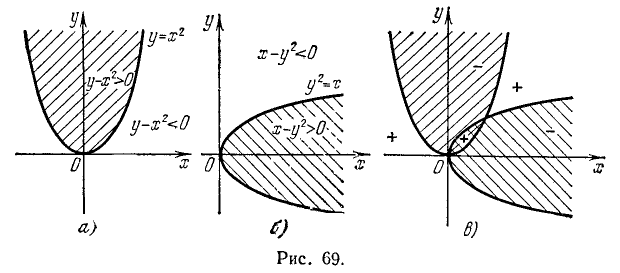
области — областями ее отрицательности. Всего получается пять областей, в двух из которых функция отрицательна и в трех положительна.
Неравенства и алгоритм их решения
В отличие от уравнений в неравенствах невозможна проверка (в обычном смысле) найденных решений. Вследствие этого схема решения, часто применявшаяся при решении уравнений, заключающаяся в получении последовательности уравнений- следствий с последующим отбором корней, при решении неравенств не работает.
Тем не менее многие приемы и методы решения неравенств совпадают с приемами и методами решения уравнений (преобразование, разложение на множители, замена неизвестного). Более того, исходя из идей метода интервалов, решение любого неравенства (во всяком случае, тех, которые встречаются в школьной практике и на конкурсном экзамене) можно свести к решению одного или нескольких уравнений. Простейшую модификацию метода интервалов иллюстрирует следующий пример.
- Решить неравенство
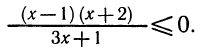
Решение:
Отметим на числовой прямой точки, в которых меняют знак (обращаются в ноль) двучлены 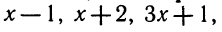 соответственно
соответственно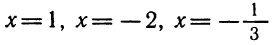 (рис. 1). При х>1 каждый из трех двучленов положителен, следовательно, положительна и вся дробь. Двигаясь вдоль прямой справа налево, замечаем, что в каждой из отмеченных точек меняет знак в точности один множитель (деление на
(рис. 1). При х>1 каждый из трех двучленов положителен, следовательно, положительна и вся дробь. Двигаясь вдоль прямой справа налево, замечаем, что в каждой из отмеченных точек меняет знак в точности один множитель (деление на 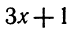 — это умножение на
— это умножение на 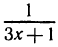 ). Следовательно, меняет знак и левая часть нашего неравенства.
). Следовательно, меняет знак и левая часть нашего неравенства.
Ответ. 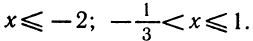
В общем случае метод интервалов основывается на следующем простом рассуждении. Пусть задана функция f (х), тогда числовую прямую можно разбить на четыре множества. А — множество
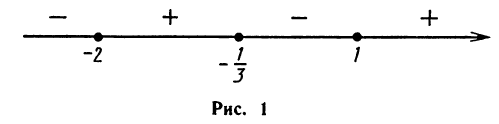
точек, для которых f (x)>0; В — множество точек, для которых f (х) = 0; С — множество точек, для которых f (х)<0; D — множество точек, для которых f (х) не определена. Как правило, каждое из множеств представляет собой объединение точек, лучей и отрезков (с концами или без). Большей частью множество В состоит из отдельных точек.
Решение неравенств вида  можно разбить на следующие этапы. Сначала находим граничные точки множеств Л, В, С и D, для чего решаем соответствующие уравнения (в большинстве случаев множество В состоит из точек, являющихся граничными для Л и С). Найденные точки разбивают прямую на лучи и интервалы. Теперь для каждого луча или интервала определяем, к какому из четырех множеств относятся принадлежащие ему точки. (Лучше эти операции осуществлять последовательно. Например, сначала найти множество D, затем В и т. д.)
можно разбить на следующие этапы. Сначала находим граничные точки множеств Л, В, С и D, для чего решаем соответствующие уравнения (в большинстве случаев множество В состоит из точек, являющихся граничными для Л и С). Найденные точки разбивают прямую на лучи и интервалы. Теперь для каждого луча или интервала определяем, к какому из четырех множеств относятся принадлежащие ему точки. (Лучше эти операции осуществлять последовательно. Например, сначала найти множество D, затем В и т. д.)
2. Решить неравенство 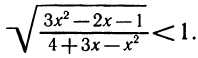
Решение:
Найдем значения х, для которых обращается в ноль соответственно числитель или знаменатель данной дроби:  Отметим найденные точки на числовой прямой. В этих точках подкоренное выражение меняет знак. Поскольку при х>4 оно отрицательно, расставляем знаки, как показано на рисунке 2, а. Левая часть данного неравенства
Отметим найденные точки на числовой прямой. В этих точках подкоренное выражение меняет знак. Поскольку при х>4 оно отрицательно, расставляем знаки, как показано на рисунке 2, а. Левая часть данного неравенства
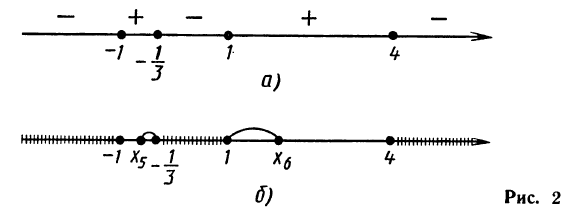
определена при 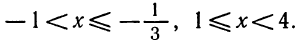 Теперь решим уравнение
Теперь решим уравнение
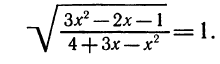
Найдем 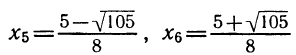 и нанесем эти значения на числовую прямую. Из нее нас интересуют лишь оставшиеся два полуинтервала (на рис. 2,б они не заштрихованы). Эти точки разбили каждый из наших полуинтервалов на две части: в одной выполняется искомое неравенство, в другой — нет. (Формально можно поступить так: обе части данного неравенства возводим в квадрат, переносим 1 в левую часть, приводим к общему знаменателю. Тогда найденные значения
и нанесем эти значения на числовую прямую. Из нее нас интересуют лишь оставшиеся два полуинтервала (на рис. 2,б они не заштрихованы). Эти точки разбили каждый из наших полуинтервалов на две части: в одной выполняется искомое неравенство, в другой — нет. (Формально можно поступить так: обе части данного неравенства возводим в квадрат, переносим 1 в левую часть, приводим к общему знаменателю. Тогда найденные значения  есть нули числи теля получившейся дроби. В них происходит смена знака.) При х= 1 и
есть нули числи теля получившейся дроби. В них происходит смена знака.) При х= 1 и 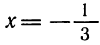 — неравенство выполняется.
— неравенство выполняется.
Ответ. 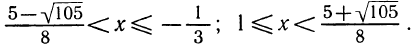
Удобно при решении неравенства методом интервалов, находя точки, в которых меняет знак какой-либо множитель, отмечать эти точки черточкой. Тогда, если в какой-то точке меняют знак нечетное число множителей (стоит нечетное число черточек), знак всего выражения меняется; если же знак меняют четное число множителей (стоит четное число черточек), знак сохраняется.
3. Решить неравенство 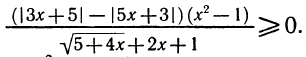
Решение:
Множитель 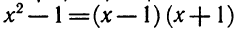 обращается в ноль и меняет знак в точках ±1. В этих же точках обращается в ноль и множитель
обращается в ноль и меняет знак в точках ±1. В этих же точках обращается в ноль и множитель  Нетрудно доказать, что он также меняет знак. Уравнение
Нетрудно доказать, что он также меняет знак. Уравнение 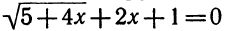 имеет один корень х = — 1, при переходе через который выражение
имеет один корень х = — 1, при переходе через который выражение 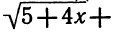
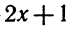

меняет знак с минуса на плюс, если двигаться слева направо. (Докажите.) Теперь расставляем знаки (рис. 3).
Ответ. 
Преобразование неравенств
Многие виды преобразований, которыми мы пользуемся при решении уравнений, так как они или приводят к эквивалентному уравнению, или, в крайнем случае, к уравнению-следствию, оказываются запрещенными при решении неравенств.
4. Решить неравенство 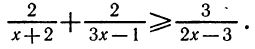
Решение:
При решении этого неравенства грубой ошибкой было бы освобождение от знаменателя (с сохранением знака не равенства). Стандартный путь: перенесем все в одну часть (левую) , приведем к общему знаменателю, а затем разложим на множители числитель. Получим
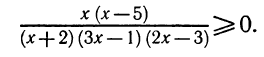
Получившееся неравенство решается методом интервалов.
Ответ. 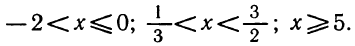
При решении неравенств, содержащих квадратные радикалы, необходимо твердо запомнить что возводить их в квадрат, сохраняя знак неравенства, можно лишь при условии неотрицательности обеих частей. (Возможна, правда, и другая, более редкая ситуация, когда обе части неположительны. В этом случае знак не равенства меняется на противоположный.) В других случаях воз можно как приобретение лишних решений, так и потеря решений. (Ясно, что если при одном знаке неравенства между левой и правой частями решения добавляются, то при противоположном теряются.) Рассмотрим простой пример.
5. Решить неравенство 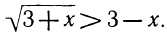
Решение:
Самый обычный путь решения состоит в рассмотрении двух случаев: 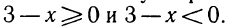 Если
Если 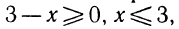 то обе части неотрицательны (при допустимых х) и можно воз водить неравенство в квадрат, сохраняя знак неравенства. Получим
то обе части неотрицательны (при допустимых х) и можно воз водить неравенство в квадрат, сохраняя знак неравенства. Получим 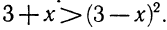 Отметим, что здесь нам нет необходимости заботиться о выполнении неравенства
Отметим, что здесь нам нет необходимости заботиться о выполнении неравенства 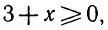 поскольку это условие автоматически выполняется для всех х, для которых
поскольку это условие автоматически выполняется для всех х, для которых 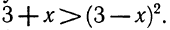 Получая квадратное неравенство, находим
Получая квадратное неравенство, находим 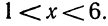 Но по условию
Но по условию 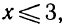 следовательно, в первом случае решением неравенства будет
следовательно, в первом случае решением неравенства будет 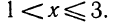
Если х>3, то правая часть неравенства отрицательна, левая положительна; подходят все х>3.
Объединяя оба случая, получаем ответ: х>1.
Очень удобно данное неравенство решать при помощи замены 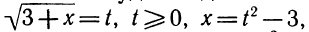 которая сразу приводит нас к квадратному неравенству
которая сразу приводит нас к квадратному неравенству 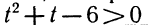 (в системе с неравенством
(в системе с неравенством  , откуда находим
, откуда находим 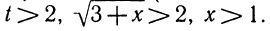
И наконец, третья возможность: исходя из идей метода интервалов, решаем уравнение 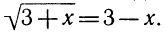 Корень один: х=1 и т. д.
Корень один: х=1 и т. д.
Ответ. 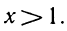
Неравенства, содержащие абсолютные величины
Обычный путь решения неравенств, содержащих абсолютные величины, состоит в том, что числовая прямая разбивается на участки, на каждом из которых на основании определения абсолютной величины знак модуля можно снять. Например:
6. Решить неравенство 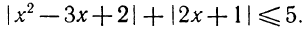
Решение:
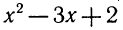 отрицателен при 1<х<2 и неотрицателен при остальных
отрицателен при 1<х<2 и неотрицателен при остальных 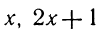 меняет знак при
меняет знак при 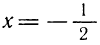 Следовательно, нам надо рассмотреть четыре случая.
Следовательно, нам надо рассмотреть четыре случая.
1.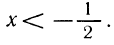 В этом случае
В этом случае 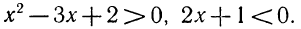 Получаем неравенство
Получаем неравенство  Его решение
Его решение 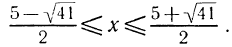 С учетом условия
С учетом условия 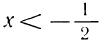 находим
находим 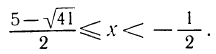
2. 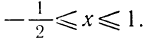 Имеем неравенство
Имеем неравенство 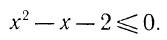 Его решение
Его решение 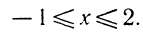 Следовательно, весь отрезок —
Следовательно, весь отрезок — 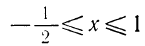 удовлетворяет неравенству.
удовлетворяет неравенству.
3.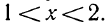 Получаем
Получаем 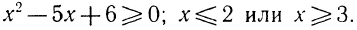 Вновь подходит весь интервал.
Вновь подходит весь интервал.
4.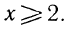 Неравенство то же, что и в случае 2. Подходит лишь х = 2.
Неравенство то же, что и в случае 2. Подходит лишь х = 2.
Ответ. 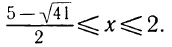
Другой подход к неравенствам, содержащим абсолютные вели чины, состоит в следующем. Неравенство 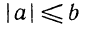 эквивалентно системе
эквивалентно системе
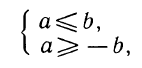
а неравенство 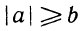 эквивалентно объединению неравенств
эквивалентно объединению неравенств
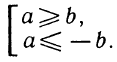
(Напомним, что в системе должны выполняться оба неравенства. Соответствует союзу «и». Объединение неравенств означает, что должно выполняться хотя бы одно из неравенств. Соответствует союзу «или».) В случае строгих неравенств все неравенства со ответственно заменяются на строгие.
Доказательства обоих утверждений без труда следуют из определения абсолютной величины. Нагляднее всего эти доказательства реализовать, интерпретируя неравенства графически, изобразив на координатной плоскости в первом случае все точки (а; b) для которых 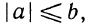 а затем — все точки, для которых
а затем — все точки, для которых
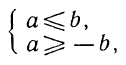
и показать совпадение этих множеств.
Аналогично для неравенства 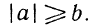
При помощи этого приема мы во многих случаях можем последовательно избавляться от знака абсолютной величины, уединяя выражения под этим знаком.
Решим, например, еще раз неравенство 6. Имеем
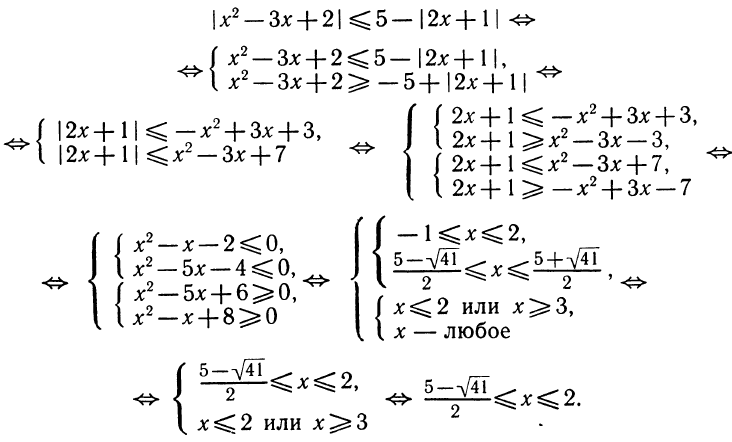
При решении этого неравенства особых преимуществ по срав нению с первым методом не видно. Однако в некоторых случаях эти преимущества весьма заметны.
7. Решить неравенство 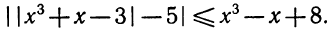
Решение:
Это неравенство не так просто решить стандартным путем. В то время как переходя к системе и т. д.» мы решим его без особого труда.
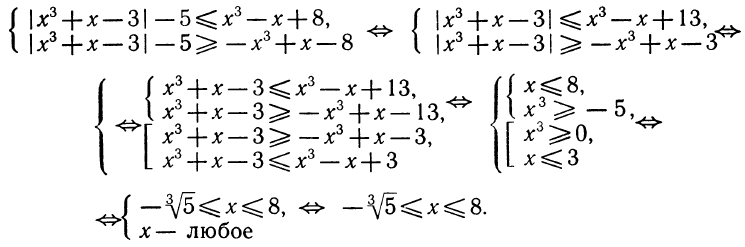
Ответ. 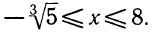
На этом мы закончим рассмотрение примеров к теме «Неравенства». В конце помещены задачи с условием «решить неравенство». Однако не стоит только ими ограничиваться. Полезно, наряду с неравенством, указанным в условии, рассмотреть три других возможных неравенства. (Например, если стоит знак >, то рассмотреть также неравенства со знаками  Полезно также рассмотреть уравнения (с одним не известным) и, заменив знак « = » на знак неравенства, решить соответствующие неравенства.
Полезно также рассмотреть уравнения (с одним не известным) и, заменив знак « = » на знак неравенства, решить соответствующие неравенства.
Решение заданий и задач по предметам:
Дополнительные лекции по высшей математике:
- Тождественные преобразования алгебраических выражений
- Функции и графики
- Преобразования графиков функций
- Квадратная функция и её графики
- Алгебраические неравенства
- Неравенства с переменными
- Прогрессии в математике
- Арифметическая прогрессия
- Геометрическая прогрессия
- Показатели в математике
- Логарифмы в математике
- Исследование уравнений
- Уравнения высших степеней
- Уравнения высших степеней с одним неизвестным
- Комплексные числа
- Непрерывная дробь (цепная дробь)
- Алгебраические уравнения
- Неопределенные уравнения
- Соединения
- Бином Ньютона
- Число е
- Непрерывные дроби
- Функция
- Исследование функций
- Предел
- Интеграл
- Двойной интеграл
- Тройной интеграл
- Интегрирование
- Неопределённый интеграл
- Определенный интеграл
- Криволинейные интегралы
- Поверхностные интегралы
- Несобственные интегралы
- Кратные интегралы
- Интегралы, зависящие от параметра
- Квадратный трехчлен
- Производная
- Применение производной к исследованию функций
- Приложения производной
- Дифференциал функции
- Дифференцирование в математике
- Формулы и правила дифференцирования
- Дифференциальное исчисление
- Дифференциальные уравнения
- Дифференциальные уравнения первого порядка
- Дифференциальные уравнения высших порядков
- Дифференциальные уравнения в частных производных
- Тригонометрические функции
- Тригонометрические уравнения и неравенства
- Показательная функция
- Показательные уравнения
- Обобщенная степень
- Взаимно обратные функции
- Логарифмическая функция
- Уравнения и неравенства
- Положительные и отрицательные числа
- Алгебраические выражения
- Иррациональные алгебраические выражения
- Преобразование алгебраических выражений
- Преобразование дробных алгебраических выражений
- Разложение многочленов на множители
- Многочлены от одного переменного
- Алгебраические дроби
- Пропорции
- Уравнения
- Системы уравнений
- Системы уравнений высших степеней
- Системы алгебраических уравнений
- Системы линейных уравнений
- Системы дифференциальных уравнений
- Арифметический квадратный корень
- Квадратные и кубические корни
- Извлечение квадратного корня
- Рациональные числа
- Иррациональные числа
- Арифметический корень
- Квадратные уравнения
- Иррациональные уравнения
- Последовательность
- Ряды сходящиеся и расходящиеся
- Тригонометрические функции произвольного угла
- Тригонометрические формулы
- Обратные тригонометрические функции
- Теорема Безу
- Математическая индукция
- Показатель степени
- Показательные функции и логарифмы
- Множество
- Множество действительных чисел
- Числовые множества
- Преобразование рациональных выражений
- Преобразование иррациональных выражений
- Геометрия
- Действительные числа
- Степени и корни
- Степень с рациональным показателем
- Тригонометрические функции угла
- Тригонометрические функции числового аргумента
- Тригонометрические выражения и их преобразования
- Преобразование тригонометрических выражений
- Комбинаторика
- Вычислительная математика
- Прямая линия на плоскости и ее уравнения
- Прямая и плоскость
- Линии и уравнения
- Прямая линия
- Уравнения прямой и плоскости в пространстве
- Кривые второго порядка
- Кривые и поверхности второго порядка
- Числовые ряды
- Степенные ряды
- Ряды Фурье
- Преобразование Фурье
- Функциональные ряды
- Функции многих переменных
- Метод координат
- Гармонический анализ
- Вещественные числа
- Предел последовательности
- Аналитическая геометрия
- Аналитическая геометрия на плоскости
- Аналитическая геометрия в пространстве
- Функции одной переменной
- Высшая алгебра
- Векторная алгебра
- Векторный анализ
- Векторы
- Скалярное произведение векторов
- Векторное произведение векторов
- Смешанное произведение векторов
- Операции над векторами
- Непрерывность функций
- Предел и непрерывность функций нескольких переменных
- Предел и непрерывность функции одной переменной
- Производные и дифференциалы функции одной переменной
- Частные производные и дифференцируемость функций нескольких переменных
- Дифференциальное исчисление функции одной переменной
- Матрицы
- Линейные и евклидовы пространства
- Линейные отображения
- Дифференциальные теоремы о среднем
- Теория устойчивости дифференциальных уравнений
- Функции комплексного переменного
- Преобразование Лапласа
- Теории поля
- Операционное исчисление
- Системы координат
- Рациональная функция
- Интегральное исчисление
- Интегральное исчисление функций одной переменной
- Дифференциальное исчисление функций нескольких переменных
- Отношение в математике
- Математическая логика
- Графы в математике
- Линейные пространства
- Первообразная и неопределенный интеграл
- Линейная функция
- Выпуклые множества точек
- Система координат
