Оглавление:
Обобщенная степень
Выражение 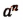 при первом его появлении имело смысл лишь при целом положительном значении буквы n. Например, под
при первом его появлении имело смысл лишь при целом положительном значении буквы n. Например, под 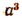 мы понимали произведение
мы понимали произведение 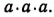 Все действия над выражениями вида
Все действия над выражениями вида 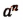 были выведены в предположении, что показатели степеней — целые положительные числа (см. стр. 67 и 71). Далее в § 8 гл. IX мы приняли следующие определения:
были выведены в предположении, что показатели степеней — целые положительные числа (см. стр. 67 и 71). Далее в § 8 гл. IX мы приняли следующие определения:
- Если
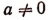 , то
, то 
- Если
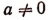 и q — целое положительное число, то
и q — целое положительное число, то
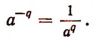
Там же было показано, что все действия над выражениями вида
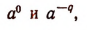
где q — целое положительное число, можно выполнять по тем же правилам, какие были установлены для выражения вида
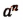 ,
,
где n — целое положительное число.
Таким образом, выражение 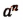 стало иметь смысл степени и тогда, когда n — нуль или целое отрицательное число. Теперь примем еще одно определение.
стало иметь смысл степени и тогда, когда n — нуль или целое отрицательное число. Теперь примем еще одно определение.
Под выражением 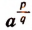 , где а > 0 и числа р и q натуральные, условимся понимать арифметическое значение следующего корня
, где а > 0 и числа р и q натуральные, условимся понимать арифметическое значение следующего корня 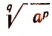 .
.
Например, 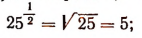
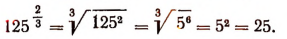
Таким образом, выражение 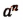 стало иметь смысл и тогда, когда n есть дробное положительное число.
стало иметь смысл и тогда, когда n есть дробное положительное число.
Легко убедиться в том, что действия над выражениями вида 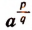 можно производить также по тем правилам, которые были установлены для степеней, имеющих целые показатели. Действительно,
можно производить также по тем правилам, которые были установлены для степеней, имеющих целые показатели. Действительно,
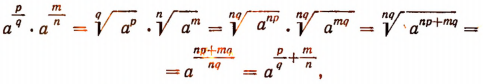
т. е. при умножении степеней с дробными показателями можно применять то же правило, что и для умножения степеней, имеющих целые показатели.
Также можно убедиться в том, что
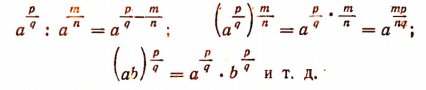
Примем по определению, что
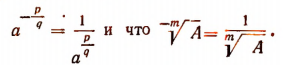
Теперь рассмотрим выражение 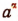 , где а > 0 и
, где а > 0 и 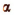 есть число иррациональное.
есть число иррациональное.
Чтобы сделать изложение более наглядным, примем а = 2 и 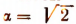 .
.
Составим последовательность
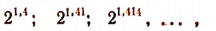
которую можно записать так:
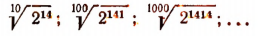
Эта возрастающая последовательность ограничена сверху (например, числом 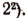 По признаку Вейерштрасса (см. стр. 408) она имеет предел, который мы и принимаем за значение выражения
По признаку Вейерштрасса (см. стр. 408) она имеет предел, который мы и принимаем за значение выражения
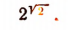
Итак, мы можем сделать следующие заключения.
Выражение 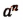 , где а > 0, имеет смысл степени при всяком действительном значении n.
, где а > 0, имеет смысл степени при всяком действительном значении n.
Выражение 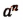 при всяком действительном значении n будем называть обобщенной степенью.
при всяком действительном значении n будем называть обобщенной степенью.
Для обобщенных степеней справедливы правила, установленные ранее для степеней с натуральными показателями.
Примеры:
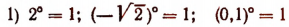 (напоминаем, что выражение 0° смысла не имеет).
(напоминаем, что выражение 0° смысла не имеет).
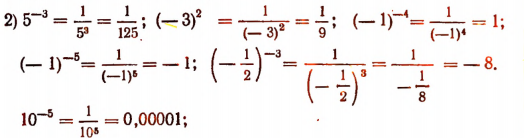
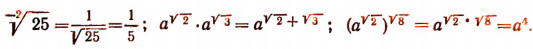
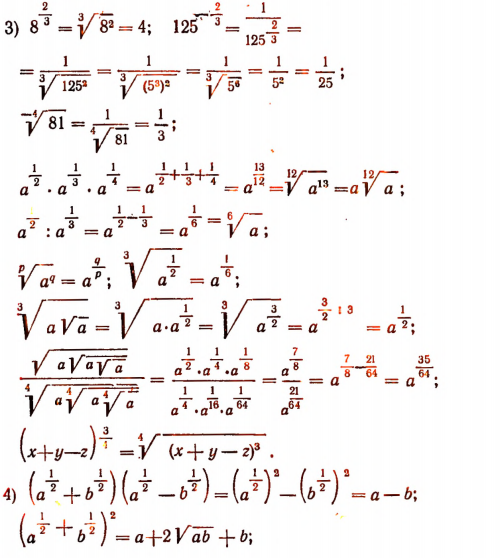
Измерение одночлена
Пусть имеется произведение степеней каких-либо букв с числовым коэффициентом, который может быть и единицей, но не нулем.
Тогда измерением такого произведения (или одночлена) называется сумма показателей степеней всех входящих в это произведение букв.
Примеры:
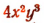 есть одночлен 5-го измерения,
есть одночлен 5-го измерения,
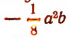 есть одночлен 3-го измерения,
есть одночлен 3-го измерения,
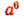 есть одночлен 6-го измерения,
есть одночлен 6-го измерения,
а есть одночлен 1-го измерения,
abxy есть одночлен 4-го измерения,
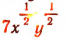 есть одночлен 1-го измерения.
есть одночлен 1-го измерения.
Одночлен 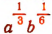 имеет измерение, равное
имеет измерение, равное 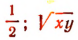 есть одночлен 1-го измерения, так как
есть одночлен 1-го измерения, так как
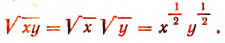
Одночлен 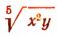 имеет измерение, равное
имеет измерение, равное 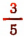 , так как
, так как
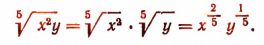
Но иногда приходится рассматривать измерение одночлена не по отношению ко всем входящим в него буквам, а лишь по отношению к некоторым избранным.
Примеры:
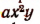 есть одночлен 3-го измерения относительно х и у,
есть одночлен 3-го измерения относительно х и у,
axby есть одночлен 2-го измерения относительно х и у,
ax есть одночлен 1-го измерения относительно х.
Однородные многочлены
Определение. Многочлен называется однородным относительно каких-либо букв, если все его члены имеют одинаковое измерение относительно этих букв.
Примеры:

§ 3. ПОКАЗАТЕЛЬНАЯ ФУНКЦИЯ
Выражение 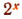 есть функция независимой переменной х, так как каждому значению х соответствует определенное значение выражения
есть функция независимой переменной х, так как каждому значению х соответствует определенное значение выражения 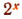 .
.
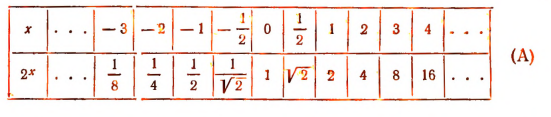
Составим таблицу значении функции 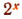 при некоторых значениях х.
при некоторых значениях х.
Если 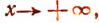 то
то  . Если
. Если  , то
, то  , никогда не достигая нуля.
, никогда не достигая нуля.
Ни при каком значении х функция 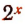 не может принять отрицательного значения или значение, равное нулю, т. е. всегда
не может принять отрицательного значения или значение, равное нулю, т. е. всегда
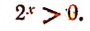
Если x>0, то 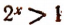 . Если x = 0, то
. Если x = 0, то 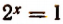 .
.
Если х<0, то  . Если
. Если  то
то 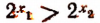 .
.
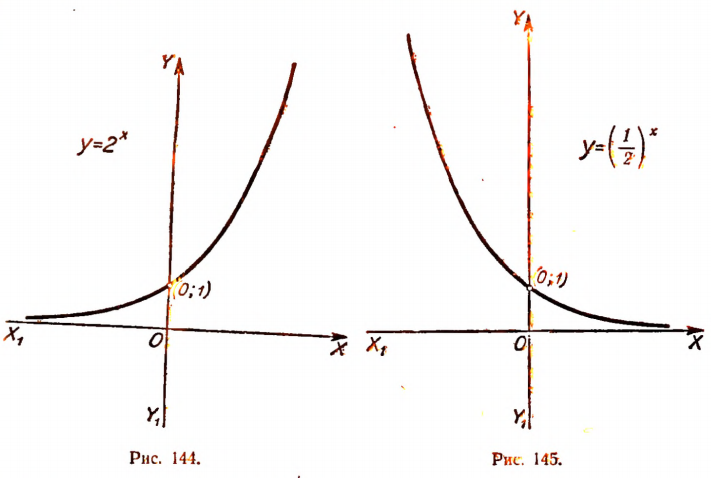
График функции 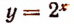 изображен на рисунке 144.
изображен на рисунке 144.
Составим таблицу значений функции 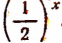
Если  , никогда не достигая нуля.
, никогда не достигая нуля.
Если 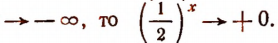
Ни при каком значении х функция 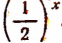 не может принять отрицательного значения или обратиться в нуль, т. е. всегда
не может принять отрицательного значения или обратиться в нуль, т. е. всегда
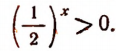
Если 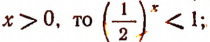 если же
если же 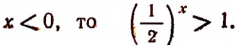
График функции 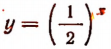 изображен на рисунке 145.
изображен на рисунке 145.
Выражение 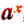 , где а есть данное положительное число, а х — независимая переменная, называется пока-зательной функцией (простейшей).
, где а есть данное положительное число, а х — независимая переменная, называется пока-зательной функцией (простейшей).
Показательными функциями являются и такие функции, как 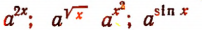 и т. д.
и т. д.
Определение:
Показательной функцией называется такая степень, основанием которой служит данное положительное число, а показателем — величина, зависящая от какого-либо аргумента, например от х.
Примечание:
Если же основание степени зависит от какого-либо аргумента, например от х, а показатель степени —данное число, то такая степень не называется показательной функцией, а называется степенной функцией.
Например, 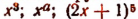 суть функции степенные, а не показательные.
суть функции степенные, а не показательные.
Свойства показательной функции 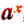 при а > 1
при а > 1
- При всяком действительном значении х,
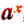 > О,
> О, - Если х < 0, то
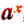 <1.
<1. - Если х = 0, то
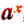 = 1.
= 1. - Если х > 0, то
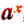 > 1.
> 1. - Если
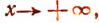 то
то 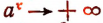 .
. - Если
 , то
, то  .
. - Если
 то
то 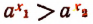 .
.
Все эти свойства легко усмотреть из таблицы (А), в которой были приведены значения показательной функции 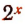 .
.
Не останавливаясь на доказательстве всех свойств показательной функции 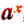 при a> 1, мы докажем в качестве иллюстрации, например, 4-е и 7-е свойства (свойство 5-е уже доказано на стр. 419).
при a> 1, мы докажем в качестве иллюстрации, например, 4-е и 7-е свойства (свойство 5-е уже доказано на стр. 419).
Теорема:
Если а > 1 и х > 0, то 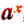 > 1.
> 1.
Мы ограничимся доказательством этой теоремы лишь для рациональных значений х.
Доказательство:
Пусть
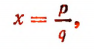
где р и q — натуральные числа.
Тогда
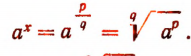
Так как 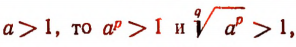 т. е.
т. е.
а*> 1,
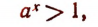
что и требовалось доказать.
Теорема:
Если а>1 и  то
то 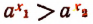 .
.
Доказательство:
Вынося за скобки множитель 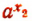 , получим, что
, получим, что
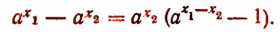
Так как а > 1 и  , то по предыдущей теореме
, то по предыдущей теореме 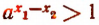 , а потому разность
, а потому разность 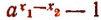 будет числом положительным. Кроме того,
будет числом положительным. Кроме того, 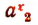 также есть чисто положительное. Отсюда следует, что
также есть чисто положительное. Отсюда следует, что 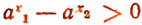 , т. е. что
, т. е. что 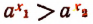 , что и требовалось доказать.
, что и требовалось доказать.
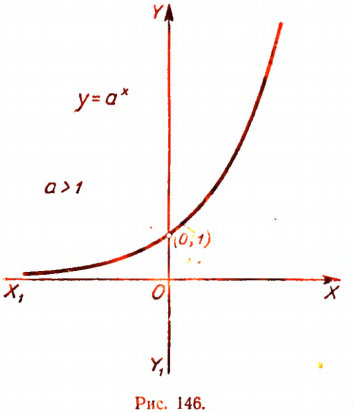
График функции 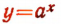 при а > 1 изображен на рисунке 146.
при а > 1 изображен на рисунке 146.
Описание графика функции 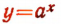 при
при
а > 1
1.Весь график лежит в верхней полуплоскости и состоит из одной ветви, простирающейся бесконечно вверх и вправо.
2.Слева график неограниченно приближается к оси 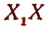 , никогда ее не достигая, а справа круто поднимается вверх.
, никогда ее не достигая, а справа круто поднимается вверх.
3. При всяком значении буквы а график проходит через точку (0, 1).
4. Всякая прямая, параллельная оси OY, пересекает график, и притом только в одной точке.
5. Всякая прямая, параллельная оси 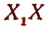 , расположенная в верхней полуплоскости, пересекает график, и притом только в одной точке.
, расположенная в верхней полуплоскости, пересекает график, и притом только в одной точке.
6. Из двух точек графика выше расположена та, которая лежит правее.
Свойства показательной функции 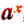 при 0 < a < 1
при 0 < a < 1
Выражение 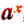 является положительным числом при всяком действительном значении х. Если х > 0, то
является положительным числом при всяком действительном значении х. Если х > 0, то 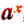 < 1. Если же х = 0, то
< 1. Если же х = 0, то
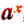 = 1.
= 1.
Если х<0, то 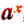 >1. Если
>1. Если 
Если  Если
Если 
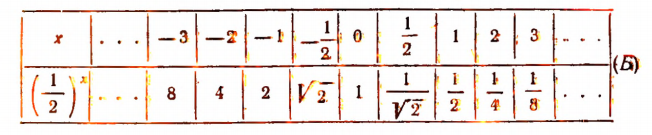
Все эти свойства легко усмотреть из таблицы (Б), в которой были приведены значения показательной функции 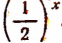 .
.
Свойства функции 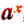 при а< 1 вытекают из свойств функции
при а< 1 вытекают из свойств функции 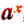 при а > 1, как их следствия.
при а > 1, как их следствия.
Докажем, например, 7-е свойство. Пусть 0<а<1 и 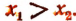
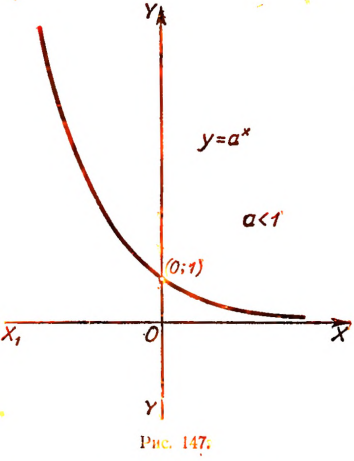
Положим, что 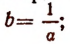 тогда будет b> 1 и мы получим, что
тогда будет b> 1 и мы получим, что
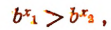
или 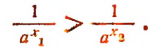
Отсюда  что и требовалось доказать.
что и требовалось доказать.
На рисунке 147 изображен график функции 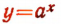 при 0<а<1. Предлагается учащемуся дать описание этого графика самостоятельно.
при 0<а<1. Предлагается учащемуся дать описание этого графика самостоятельно.
Решение заданий и задач по предметам:
Дополнительные лекции по высшей математике:
- Тождественные преобразования алгебраических выражений
- Функции и графики
- Преобразования графиков функций
- Квадратная функция и её графики
- Алгебраические неравенства
- Неравенства
- Неравенства с переменными
- Прогрессии в математике
- Арифметическая прогрессия
- Геометрическая прогрессия
- Показатели в математике
- Логарифмы в математике
- Исследование уравнений
- Уравнения высших степеней
- Уравнения высших степеней с одним неизвестным
- Комплексные числа
- Непрерывная дробь (цепная дробь)
- Алгебраические уравнения
- Неопределенные уравнения
- Соединения
- Бином Ньютона
- Число е
- Непрерывные дроби
- Функция
- Исследование функций
- Предел
- Интеграл
- Двойной интеграл
- Тройной интеграл
- Интегрирование
- Неопределённый интеграл
- Определенный интеграл
- Криволинейные интегралы
- Поверхностные интегралы
- Несобственные интегралы
- Кратные интегралы
- Интегралы, зависящие от параметра
- Квадратный трехчлен
- Производная
- Применение производной к исследованию функций
- Приложения производной
- Дифференциал функции
- Дифференцирование в математике
- Формулы и правила дифференцирования
- Дифференциальное исчисление
- Дифференциальные уравнения
- Дифференциальные уравнения первого порядка
- Дифференциальные уравнения высших порядков
- Дифференциальные уравнения в частных производных
- Тригонометрические функции
- Тригонометрические уравнения и неравенства
- Показательная функция
- Показательные уравнения
- Взаимно обратные функции
- Логарифмическая функция
- Уравнения и неравенства
- Положительные и отрицательные числа
- Алгебраические выражения
- Иррациональные алгебраические выражения
- Преобразование алгебраических выражений
- Преобразование дробных алгебраических выражений
- Разложение многочленов на множители
- Многочлены от одного переменного
- Алгебраические дроби
- Пропорции
- Уравнения
- Системы уравнений
- Системы уравнений высших степеней
- Системы алгебраических уравнений
- Системы линейных уравнений
- Системы дифференциальных уравнений
- Арифметический квадратный корень
- Квадратные и кубические корни
- Извлечение квадратного корня
- Рациональные числа
- Иррациональные числа
- Арифметический корень
- Квадратные уравнения
- Иррациональные уравнения
- Последовательность
- Ряды сходящиеся и расходящиеся
- Тригонометрические функции произвольного угла
- Тригонометрические формулы
- Обратные тригонометрические функции
- Теорема Безу
- Математическая индукция
- Показатель степени
- Показательные функции и логарифмы
- Множество
- Множество действительных чисел
- Числовые множества
- Преобразование рациональных выражений
- Преобразование иррациональных выражений
- Геометрия
- Действительные числа
- Степени и корни
- Степень с рациональным показателем
- Тригонометрические функции угла
- Тригонометрические функции числового аргумента
- Тригонометрические выражения и их преобразования
- Преобразование тригонометрических выражений
- Комбинаторика
- Вычислительная математика
- Прямая линия на плоскости и ее уравнения
- Прямая и плоскость
- Линии и уравнения
- Прямая линия
- Уравнения прямой и плоскости в пространстве
- Кривые второго порядка
- Кривые и поверхности второго порядка
- Числовые ряды
- Степенные ряды
- Ряды Фурье
- Преобразование Фурье
- Функциональные ряды
- Функции многих переменных
- Метод координат
- Гармонический анализ
- Вещественные числа
- Предел последовательности
- Аналитическая геометрия
- Аналитическая геометрия на плоскости
- Аналитическая геометрия в пространстве
- Функции одной переменной
- Высшая алгебра
- Векторная алгебра
- Векторный анализ
- Векторы
- Скалярное произведение векторов
- Векторное произведение векторов
- Смешанное произведение векторов
- Операции над векторами
- Непрерывность функций
- Предел и непрерывность функций нескольких переменных
- Предел и непрерывность функции одной переменной
- Производные и дифференциалы функции одной переменной
- Частные производные и дифференцируемость функций нескольких переменных
- Дифференциальное исчисление функции одной переменной
- Матрицы
- Линейные и евклидовы пространства
- Линейные отображения
- Дифференциальные теоремы о среднем
- Теория устойчивости дифференциальных уравнений
- Функции комплексного переменного
- Преобразование Лапласа
- Теории поля
- Операционное исчисление
- Системы координат
- Рациональная функция
- Интегральное исчисление
- Интегральное исчисление функций одной переменной
- Дифференциальное исчисление функций нескольких переменных
- Отношение в математике
- Математическая логика
- Графы в математике
- Линейные пространства
- Первообразная и неопределенный интеграл
- Линейная функция
- Выпуклые множества точек
- Система координат
