Оглавление:
Дедукцией называется переход от общего утверждения к частному. Приведем пример.
Площадь всякого треугольника равна
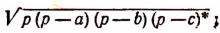
это утверждение общее.
От этого общего утверждения можно сделать переход к частному утверждению, например такому:
площадь равностороннего треугольника равна
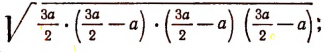
т. е. равна 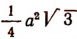 , где а — длина стороны равностороннего треугольника.
, где а — длина стороны равностороннего треугольника.
Дедукция есть одна из форм умозаключения. (Дедукция происходит от латинского слова «deductio» — выведение.)
Индукцией называется переход от частного утверждения к общему. Индукция есть также одна из форм умозаключения, применяя которую от знания отдельного факта идут к обобщению, к общему положению. (Индукция происходит от латинского слова «inductio» — наведение, побуждение.)
Все формы умозаключения связаны между собой, а потому связаны между собой дедукция и индукция. Одна дедукция (или одна индукция) никогда не может обеспечить познания объективной действительности.
Легкомысленное применение индукции может привести к неправильным выводам. Приведем пример.
Рассмотрим выражение
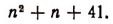
Подставив в это выражение вместо п нуль, получим простое число 41. Подставив вместо п единицу, получим 43, т. е. опять простое число. Продолжая подставлять вместо п последовательно 2; 3; 4; 5; 6; 7; 8; 9; 10; 11, получим соответственно 47, 53; 61; 71; 83; 97; 113; 131 151; 173, т. е. опять же числа простые. Можем ли мы теперь быть уверенными в справедливости такого утверждения:
«Выражение 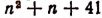 принимает значение, равное простому числу при любом целом положительном значении буквы п»?
принимает значение, равное простому числу при любом целом положительном значении буквы п»?
Быть уверенными в справедливости этого утверждения мы не можем, так как полученные выше результаты не являются достаточным основанием для такого утверждения. Они являются лишь основанием для предположения о верности этого утверждения. В действительности более полное исследование выражения 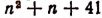 показывает, что значение этого выражения не при всяком целом значении п является простым числом. Например, при п= 40 получается число 1681, которое уже не является простым. (Число 1681 делится на 41.)
показывает, что значение этого выражения не при всяком целом значении п является простым числом. Например, при п= 40 получается число 1681, которое уже не является простым. (Число 1681 делится на 41.)
Этот пример показывает, что утверждение может быть верным при одних значениях натурального числа п и неверным при других.
Математическая индукция есть весьма общий метод, позволяющий во многих случаях исследовать законность перехода от частного утверждения к утверждению общему.
Принцип математической индукции можно сформулировать следующим образом.
Теорема о математической индукции
Пусть S(n)—некоторое утверждение, в формулировку которого входнт натуральное число п. Пусть, во-первых, утверждение  справедливо и пусть, во-вторых, из справедливости утверждения S(k), где k есть тоже любое натуральное число, не меньшее
справедливо и пусть, во-вторых, из справедливости утверждения S(k), где k есть тоже любое натуральное число, не меньшее 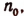 следует справедливость утверждения S(k + 1). Тогда утверждение S(n) справедливо при любом
следует справедливость утверждения S(k + 1). Тогда утверждение S(n) справедливо при любом 
Доказательство:
Допустим, что утверждение S(n) не справедливо при некотором 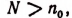 т. е. что утверждение S(N) ложно. Тогда должно быть ложным и утверждение S(N — 1), так как в противном случае из справедливости S(N — 1) по второму условию теоремы следовала бы справедливость и утверждения S(N). Точно так же убеждаемся, что из ложности S(N— 1) следует ложность S(N — 2), а из этого ложность
т. е. что утверждение S(N) ложно. Тогда должно быть ложным и утверждение S(N — 1), так как в противном случае из справедливости S(N — 1) по второму условию теоремы следовала бы справедливость и утверждения S(N). Точно так же убеждаемся, что из ложности S(N— 1) следует ложность S(N — 2), а из этого ложность
S(N —3) и т. д.
Таким образом (каким бы большим ни было число N), мы рано или поздно, отнимая от этого числа по единице, дойдем до числа 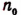 и получим, что утверждение
и получим, что утверждение  ложно, что противоречит первому условию теоремы. Полученное противоречие доказывает справедливость теоремы.
ложно, что противоречит первому условию теоремы. Полученное противоречие доказывает справедливость теоремы.
Приведенное доказательство теоремы о математической индукции может показаться некоторым читателям труднопонимаемым. Поэтому ниже приводится несколько упрощенная схема метода математической индукции.
Если в утверждении некоторой теоремы фигурирует целое положительное число п и если из справедливости этой теоремы для какого угодно частного значения п = k следует справедливость ее для значения k + 1, то, коль скоро это утверждение справедливо для п — 1, оно будет справедливо для любого целого положительного числа п.
Здесь дело обстоит так. Сначала мы убеждаемся в том, что теорема верна при п = 1. Затем, предполагая, что она верна для какого угодно частного значения п = k, доказываем ее справедливость для п = k + 1.
После этого рассуждаем так: поскольку теорема верна для п = 1, значит, она будет верной и для п — 1 + 1, т. е. для п = 2. Поскольку она верна для п = 2, она будет верной и для п = 2 + 1, т. е. для п = 3 и т. д.
Применение метода математической индукции
Примеры:
1. Доказать, что 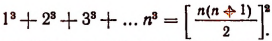
Этой формулой утверждается следующее: для того чтобы найти сумму кубов нескольких первых натуральных чисел, надо последнее из них умножить на число, большее его на единицу, полученное произведение разделить на 2 и возвести в квадрат.
Доказательство:
1. При п = 1 утверждение справедливо,
так как 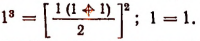
2. Допустим, что утверждение справедливо при п = k, т. е
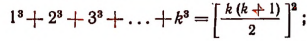
Тогда
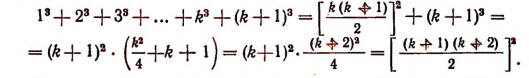
Утверждение оказалось верным и для п =k+1. Следовательно, теорема верна при всяком целом положительном значении п.
Доказать, что
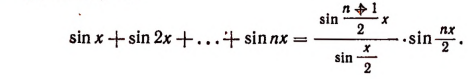
Доказательство:
1. При п = 1 утверждение справедливо, так как
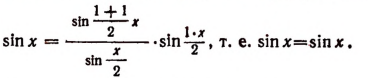
2. Допустим, что утверждение справедливо при п = k, т. е.
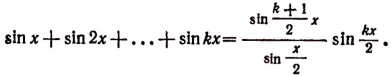
Тогда
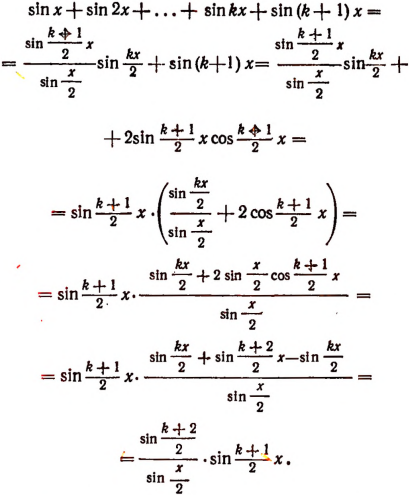
Утверждение оказалось верным и для п = k + 1. Следовательно, формула верна при всяком целом положительном значении п.
3. Доказать, что при п > 1
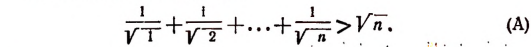
Доказательство:
При п = 2 утверждение справедливо.
Действительно,
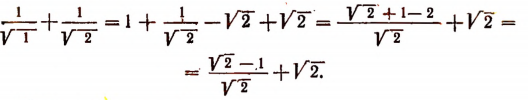
Итак, оказалось, что
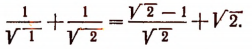
Но 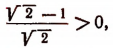 а потому
а потому 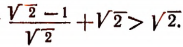
Следовательно,
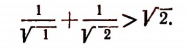
Пусть
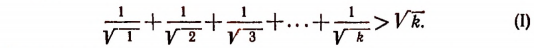
Докажем, что тогда будет справедливым и неравенство:
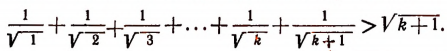
К обеим частям неравенства (I) прибавим по 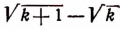 . Тогда получим:
. Тогда получим:
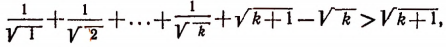
или
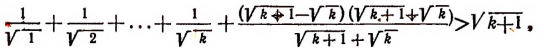
или
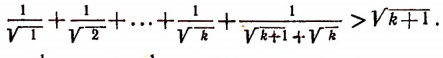
Но 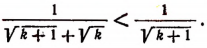 Поэтому и подавно
Поэтому и подавно
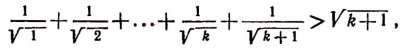
что и требовалось доказать,
Теперь мы видим, что утверждение (А) оказалось верным и для n=k+1. Следовательно, это утверждение справедливо при всяком целом положительном значении n, большем двух.
Существует очень много и других теорем, которые успешно доказываются с помощью метода математической индукции. Некоторые из таких теорем встретятся нам в последующих главах.
Доказательство неравенства
Иногда приходится применять метод математической индукции в несколько усложненной форме. Покажем это на примере. Пусть требуется доказать следующее неравенство:
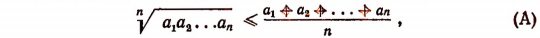
где 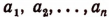 — положительные числа.
— положительные числа.
(Выражение 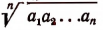 называется средним геометрическим чисел
называется средним геометрическим чисел 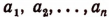 , выражение
, выражение  — их средним арифметическим.)
— их средним арифметическим.)
Во-первых, покажем справедливость неравенства (А) при n = 2.
Очевидно,что
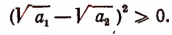
Отсюда
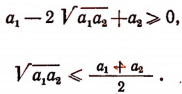
Значит, при n = 2 неравенство (А) справедливо. Теперь докажем следующую лемму.
Лемма:
Если неравенство (А) верно при п = k, то оно будет верно при n=2k.
Доказательство:
Пользуясь свойствами арифметических корней, получим:
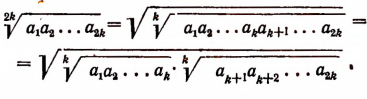
Но
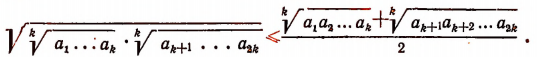
(Мы здесь воспользовались доказанным выше неравенством:
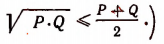
Следовательно,
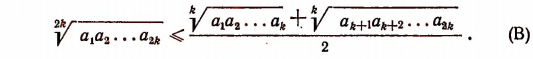
Поскольку мы предположили неравенство (А) верным при n = k, постольку
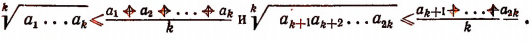
Учитывая эти два последних неравенства и неравенство (В), получим:
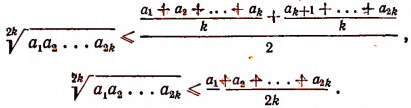
Итак, предполагая, что неравенство (А) справедливо при п = 2k, мы доказали, что оно будет справедливым и при п = 2k. Но ранее было доказано, что неравенство (А) справедливо при п = 2. Следовательно, оно будет справедливым и при п = 4,8,16, 32,…, т. е. при 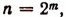 где m — любое натуральное число.
где m — любое натуральное число.
Теперь перейдем к доказательству неравенства (А) для любого натурального числа п.
Пусть п есть любое натуральное число. Если окажется, что п есть целая степень числа 2, то для такого п, как это уже было доказано, неравенство (А) справедливо. Если же п не есть целая степень числа 2, то к n всегда можно прибавить такое число q, что п+ q станет целой степенью числа 2. Итак, положим, что
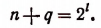
Тогда получим неравенство:
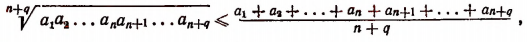
справедливое при любых положительных 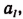 где
где
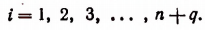
Это следует из того, что число п + q есть целая степень числа 2. Положим, что
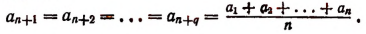
Тогда получим последовательно:
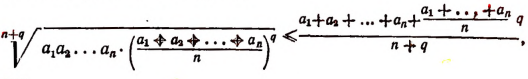
или
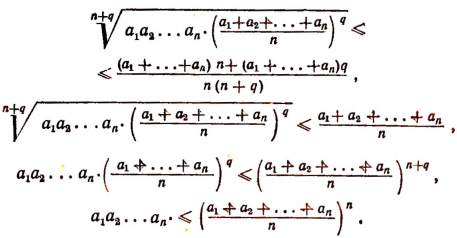
и, наконец,
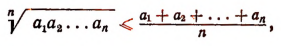
что и требовалось доказать.
Значит, неравенство (А) справедливо при всяком натуральном п.
Метод математической индукции
Метод доказательства, называемый методом математической индукции, основан на следующем принципе, который является одной из аксиом арифметики натуральных чисел.
Предложение 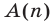 , зависящее от натуральной переменной
, зависящее от натуральной переменной 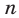 , считается истинным для всех
, считается истинным для всех 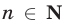 , если выполнены следующие два условия:
, если выполнены следующие два условия:
а) предложение 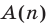 истинно для
истинно для 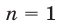 ;
;
б) из предположения, что 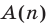 истинно для
истинно для 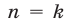 (где
(где 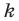 — любое натуральное число), следует, что оно истинно и для следующего значения
— любое натуральное число), следует, что оно истинно и для следующего значения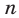 , т.е. для
, т.е. для 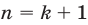 .
.
Этот принцип называется принципом математической индукции.
Под методом математической индукции понимают следующий способ доказательства: во-первых, проверяют истинность высказывания 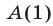 , и, во-вторых, предположив истинность высказывания
, и, во-вторых, предположив истинность высказывания 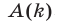 , пытаются доказать, что истинно высказывание
, пытаются доказать, что истинно высказывание 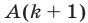 . Если это удается доказать (при любом натуральном
. Если это удается доказать (при любом натуральном 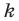 ), то предложение
), то предложение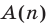 считается истинным для всех значений
считается истинным для всех значений 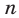 .
.
Пример:
Методом математической индукции доказать равенство
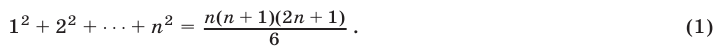
Доказательство:
При 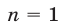 равенство (1) является верным
равенство (1) является верным 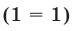 . Нужно доказать, что из предположения о том, что является верным равенство (1), следует справедливость равенства
. Нужно доказать, что из предположения о том, что является верным равенство (1), следует справедливость равенства
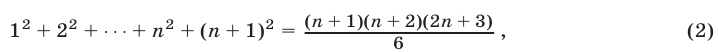
полученного из (1) заменой 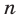 на
на 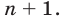
Прибавляя к обеим частям (1) слагаемое 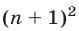 , имеем
, имеем
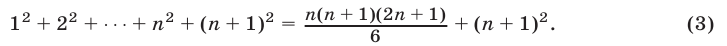
Преобразуя правую часть (3), получаем
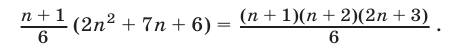
Таким образом, равенство (2) является верным, и поэтому формула (1) доказана для любого 
Дадим другое доказательство формулы (1), используя символ 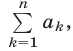 которым обозначается сумма
которым обозначается сумма 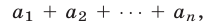 т.е.
т.е.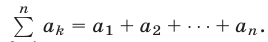 Воспользуемся тождеством
Воспользуемся тождеством

Полагая в (4) 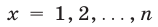 и складывая получаемые равенства, находим
и складывая получаемые равенства, находим
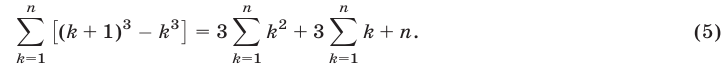
Левая часть (5) равна 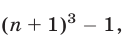 а
а 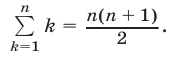 Поэтому из (5) получаем
Поэтому из (5) получаем
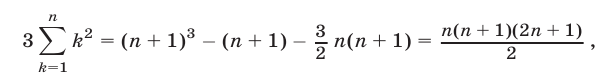
откуда следует равенство (1).
Пример:
Доказать, что для любых 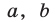 и при любом
и при любом 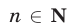 справедлива формула бинома Ньютона
справедлива формула бинома Ньютона
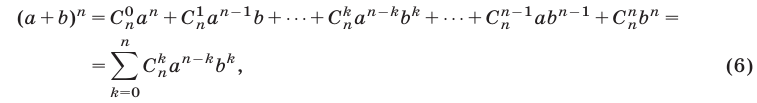
где
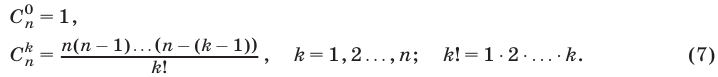
Правую часть формулы (6) называют разложением бинома, числа 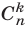 — биномиальными коэффициентами, слагаемое
— биномиальными коэффициентами, слагаемое 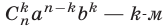 членом разложения бинома.
членом разложения бинома.
Доказательство. Воспользуемся методом математической индукции. При 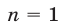 формула (6) верна, так как ее правая часть равна левой:
формула (6) верна, так как ее правая часть равна левой: 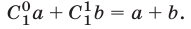
Предполагая справедливым равенство (6), докажем, что верна формула 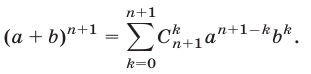
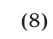
Умножая обе части равенства (6) на 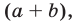 получаем
получаем
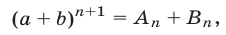
где
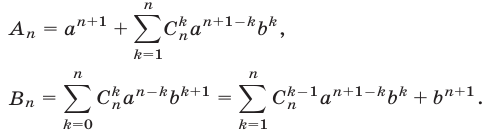
Следовательно, 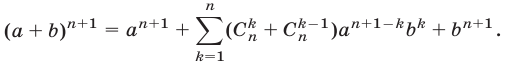
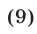
Сравнивая правые части равенств (8) и (9), заключаем, что для доказательства формулы (8) достаточно показать, что 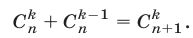
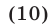
Используя (7), находим
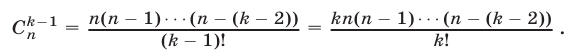
Поэтому
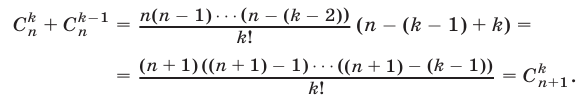
Равенство (10) доказано и поэтому справедливо равенство (8). Итак, формула (6) верна при любом  . Отметим, что
. Отметим, что
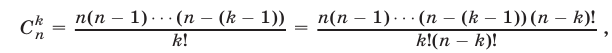
т.е. 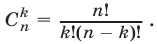
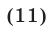
Поэтому формулу (6) можно записать в виде
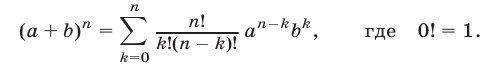
Из (11) следует, что 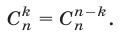
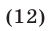 .
.
Возможно вам будут полезны эти страницы:
| Прямые и обратные теоремы примеры с решением |
| Делимость целых чисел примеры с решением |
| Рациональные числа примеры с решением |
| Множество действительных чисел примеры с решением |
Решение заданий и задач по предметам:
Дополнительные лекции по высшей математике:
- Тождественные преобразования алгебраических выражений
- Функции и графики
- Преобразования графиков функций
- Квадратная функция и её графики
- Алгебраические неравенства
- Неравенства
- Неравенства с переменными
- Прогрессии в математике
- Арифметическая прогрессия
- Геометрическая прогрессия
- Показатели в математике
- Логарифмы в математике
- Исследование уравнений
- Уравнения высших степеней
- Уравнения высших степеней с одним неизвестным
- Комплексные числа
- Непрерывная дробь (цепная дробь)
- Алгебраические уравнения
- Неопределенные уравнения
- Соединения
- Бином Ньютона
- Число е
- Непрерывные дроби
- Функция
- Исследование функций
- Предел
- Интеграл
- Двойной интеграл
- Тройной интеграл
- Интегрирование
- Неопределённый интеграл
- Определенный интеграл
- Криволинейные интегралы
- Поверхностные интегралы
- Несобственные интегралы
- Кратные интегралы
- Интегралы, зависящие от параметра
- Квадратный трехчлен
- Производная
- Применение производной к исследованию функций
- Приложения производной
- Дифференциал функции
- Дифференцирование в математике
- Формулы и правила дифференцирования
- Дифференциальное исчисление
- Дифференциальные уравнения
- Дифференциальные уравнения первого порядка
- Дифференциальные уравнения высших порядков
- Дифференциальные уравнения в частных производных
- Тригонометрические функции
- Тригонометрические уравнения и неравенства
- Показательная функция
- Показательные уравнения
- Обобщенная степень
- Взаимно обратные функции
- Логарифмическая функция
- Уравнения и неравенства
- Положительные и отрицательные числа
- Алгебраические выражения
- Иррациональные алгебраические выражения
- Преобразование алгебраических выражений
- Преобразование дробных алгебраических выражений
- Разложение многочленов на множители
- Многочлены от одного переменного
- Алгебраические дроби
- Пропорции
- Уравнения
- Системы уравнений
- Системы уравнений высших степеней
- Системы алгебраических уравнений
- Системы линейных уравнений
- Системы дифференциальных уравнений
- Арифметический квадратный корень
- Квадратные и кубические корни
- Извлечение квадратного корня
- Рациональные числа
- Иррациональные числа
- Арифметический корень
- Квадратные уравнения
- Иррациональные уравнения
- Последовательность
- Ряды сходящиеся и расходящиеся
- Тригонометрические функции произвольного угла
- Тригонометрические формулы
- Обратные тригонометрические функции
- Теорема Безу
- Показатель степени
- Показательные функции и логарифмы
- Множество
- Множество действительных чисел
- Числовые множества
- Преобразование рациональных выражений
- Преобразование иррациональных выражений
- Геометрия
- Действительные числа
- Степени и корни
- Степень с рациональным показателем
- Тригонометрические функции угла
- Тригонометрические функции числового аргумента
- Тригонометрические выражения и их преобразования
- Преобразование тригонометрических выражений
- Комбинаторика
- Вычислительная математика
- Прямая линия на плоскости и ее уравнения
- Прямая и плоскость
- Линии и уравнения
- Прямая линия
- Уравнения прямой и плоскости в пространстве
- Кривые второго порядка
- Кривые и поверхности второго порядка
- Числовые ряды
- Степенные ряды
- Ряды Фурье
- Преобразование Фурье
- Функциональные ряды
- Функции многих переменных
- Метод координат
- Гармонический анализ
- Вещественные числа
- Предел последовательности
- Аналитическая геометрия
- Аналитическая геометрия на плоскости
- Аналитическая геометрия в пространстве
- Функции одной переменной
- Высшая алгебра
- Векторная алгебра
- Векторный анализ
- Векторы
- Скалярное произведение векторов
- Векторное произведение векторов
- Смешанное произведение векторов
- Операции над векторами
- Непрерывность функций
- Предел и непрерывность функций нескольких переменных
- Предел и непрерывность функции одной переменной
- Производные и дифференциалы функции одной переменной
- Частные производные и дифференцируемость функций нескольких переменных
- Дифференциальное исчисление функции одной переменной
- Матрицы
- Линейные и евклидовы пространства
- Линейные отображения
- Дифференциальные теоремы о среднем
- Теория устойчивости дифференциальных уравнений
- Функции комплексного переменного
- Преобразование Лапласа
- Теории поля
- Операционное исчисление
- Системы координат
- Рациональная функция
- Интегральное исчисление
- Интегральное исчисление функций одной переменной
- Дифференциальное исчисление функций нескольких переменных
- Отношение в математике
- Математическая логика
- Графы в математике
- Линейные пространства
- Первообразная и неопределенный интеграл
- Линейная функция
- Выпуклые множества точек
- Система координат
