Оглавление:
Преобразования тригонометрических выражений опираются на следующие основные формулы:
- основные тригонометрические тождества
- формулы приведения
- формулы суммы и разности аргументов
- формулы двойного аргумента
- формулы тройного аргумента
- формулы половинного аргумента
- формулы преобразования суммы (разности) тригонометрических функций в произведение
- формулы преобразования произведения тригонометрических функций в сумму (разность)
Формулы сложения и вычитания
Расстояние между двумя точками на плоскости
Задача:
На плоскости даны две точки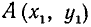 
и 
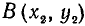. Найти расстояние АВ между ними.
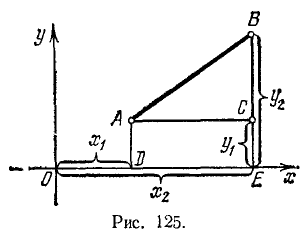
Решение:
На рис. 125 изображен случай, когда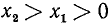 
и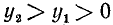 
. Мы же будем вести рассуждения, справедливые для любого случая расположения точек A и В. Заметим, что 
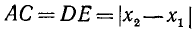и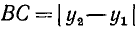 
. По теореме Пифагора из прямоугольного треугольника АСВ имеем
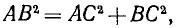
или
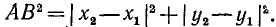
Так как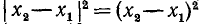 
и 
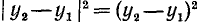, то
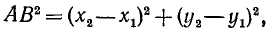
откуда имеем
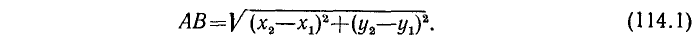
Пример:
Найти расстояние между точками А (7, —2) и В (4, — 6).
Решение:
По формуле (114.1) имеем
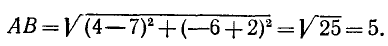
Пример:
Найти расстояние между точками С (2, —1) и D (3, 1).
Решение:
По формуле (114.1) имеем
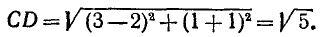
Косинус суммы и разности двух аргументов
а) Косинус разности. Предположим, что углы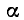 
и 
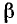удовлетворяют следующим двум условиям:
На рис. 126 изображены углы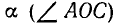 
и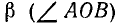 
. Точки А, В и С лежат на единичной окружности (OA = OB = ОС = 1). Заметим, что 
.
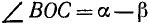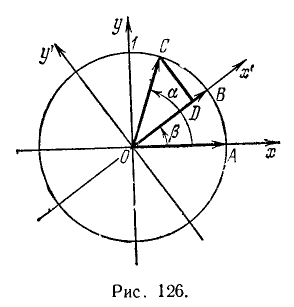
Кроме системы координат Оху будем рассматривать еще новую систему координат Ох’у’, полученную из старой поворотом на угол .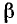
В дальнейшем будем использовать тот факт, что расстояние ВС между точками В и С, вычисленное в старой системе координат Оху и в новой системе координат Ох’у’, будет одинаково.
В системе координат Оху точка В имеет координаты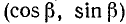 
, а точка С — координаты 
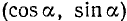. По формуле (114.1) имеем
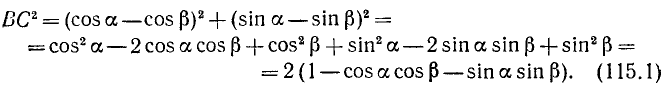
В системе координат Ох’у’ точка В имеет координаты (1, 0), а точка С — координаты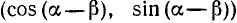 
. По формуле (114.1) найдем
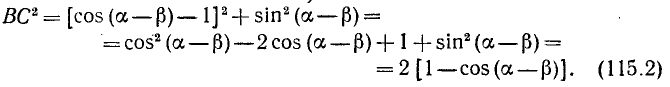
Приравняв правые части формул (115.1) и (115.2), получим выражение для косинуса разности двух углов:
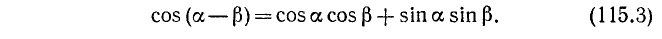
Мы доказали теорему:
Косинус разности двух углов равен произведению косинуса первого угла на косинус второго плюс произведение синуса первого угла на синус второго.
Заметим, что ограничения, наложенные на углы 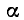и 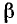условиями 1) и 2), можно снять. В самом деле, допустим, что снято ограничение 
; 
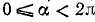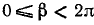, налагаемое на углы 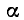и 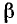условиями 1), и мы имеем: 
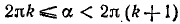и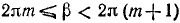 
, где k, m = 0, ±1, ±2, … , ил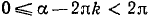и 
и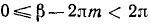 
. Положив 
, 
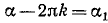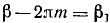, получим 
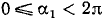и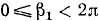 
. Без ограничения общности будем считать, что 
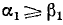. (Ниже будет показано, что условие 2) не существенно.)
Итак, углы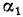 
и 
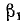, удовлетворяют условиям 1) и 2), при которых была доказана теорема. Следовательно,
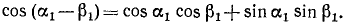
Подставив вместо 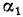и 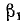их значения, получим
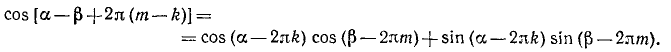
Воспользовавшись периодичностью синуса и косинуса, придем к формуле (115.3). Мы показали, что условие 1) не существенно.
Допустим теперь, что, вопреки условию 2),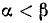 
, т. е. 
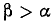. Воспользовавшись четностью косинуса, будем иметь
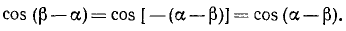
Итак, доказана общность формулы (115.3), т. е. ее справедливость при любых углах 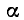и .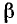
б) Косинус суммы. Так как формула (115.3) справедлива для любых двух углов 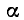и 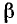, то, заменив в ней 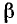на 
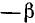, получим
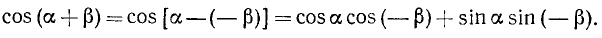
Воспользовавшись четностью косинуса и нечетностью синуса, будем иметь
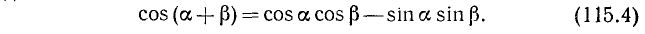
Мы доказали теорему:
Косинус суммы двух углов равен произведению косинуса первого угла на косинус второго минус произведение синуса первого угла на синус второго.
Пример:
Вычислить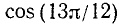 
.
Решение:
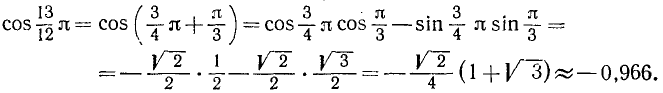
Формулы (115.3) и (115.4), как и все выводимые в дальнейшем соотношения для тригонометрических функций, сохраняют свою силу и для тригонометрических функций числового аргумента. Вообще, в дальнейшем мы уже не будем всякий раз указывать, как понимается аргумент тригонометрической функции (как угол или как число).
Синус суммы и разности двух аргументов
а) Синус суммы. Воспользовавшись формулой приведения (105.2), будем иметь
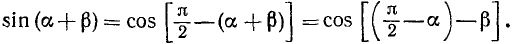
К правой части последнего равенства применим формулу (115.3):
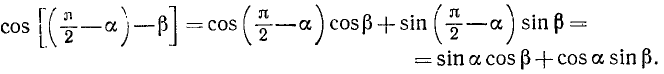
Итак,
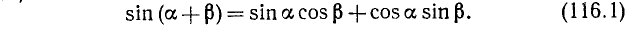
Мы доказали теорему:
Синус суммы двух аргументов равен произведению синуса первого аргумента на косинус второго плюс произведение косинуса первого аргумента на синус второго.
б) Синус разности. Выводится формула
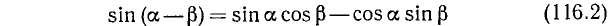
и формулируется соответствующая теорема.
Пример:
Вычислить sin 105°.
Решение:
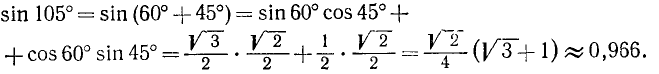
Тангенс суммы и разности двух аргументов
а) Тангенс суммы. При всех допустимых значениях аргументов 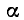и 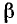имеет место формула
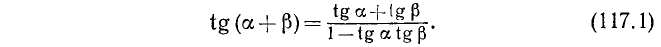
Доказательство:
Па основании формул (116.1) и (115.4) имеем
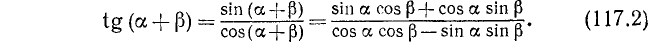
Разделив почленно числитель и знаменатель дроби, стоящей в правой части, на произведение cosaeosp (мы предполагаем, что оно отлично от нуля), получим (117.1).
б) Тангенс разности. Аналогично можно вывести формулу
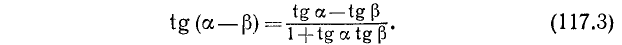
Пример:
Вычислить tg 105°.
Решение:
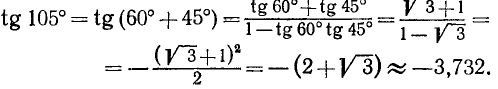
Пример:
Вычислить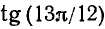 
.
Решение:
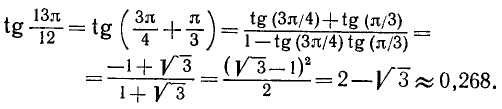
О формулах сложения для нескольких аргументов
Если возникает необходимость найти тригонометрическую функцию трех (или более) слагаемых, то это можно сделать, последовательно применив выведенные в пп. 115—117 формулы. Например:
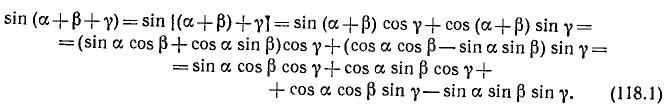
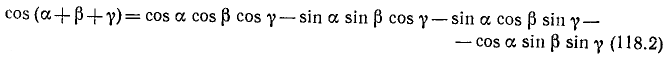
и
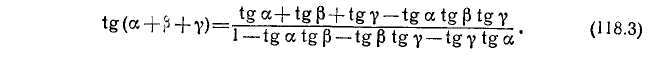
Формулы для двойного и половинного аргумента
Выражение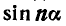 
и 
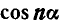через степен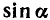и 
и 
119. Тригонометрические функции двойного аргумента. Положив в формулах (116.1), (115.4) и (117.1)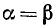 
, мы получаем следующие формулы:
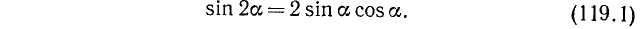
Синус двойного аргумента равен удвоенному произведению синуса и косинуса данного аргумента.
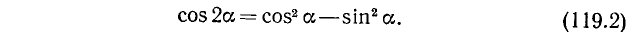
Косинус двойного аргумента равен разности квадратов косинуса и синуса данного аргумента.
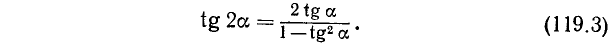
Пример:
Упростить выражение
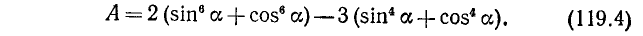
Решение:
Мы уже решали этот пример в п. 99. Используя формулы (99.9), (99.10) и (119.1), имеем
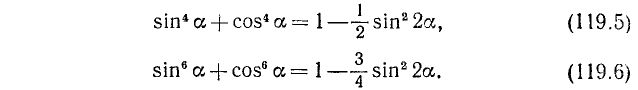
Подставив (119.5) и (119.6) в (119.4), получаем
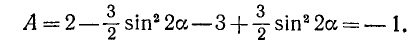
Замечание:
Формулы (119.5) и (119.6) можно получить и так:
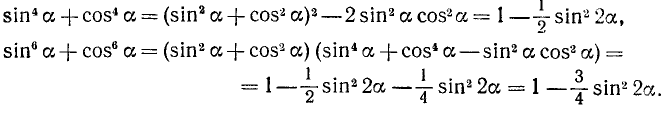
Формулы (119.1) — (119.3) можно использовать для любого аргумента 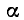, считая его двойным для аргумента 
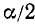. Например:
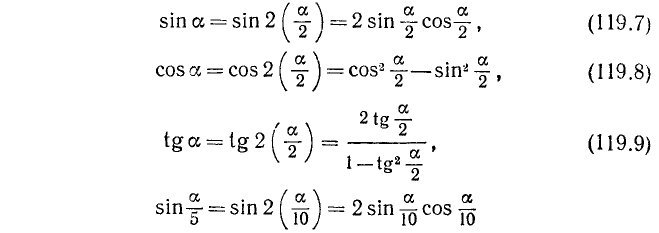
и т. д.
Пример:
Упростить выражение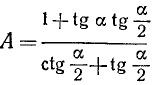 
.
Решение:
Умножим числитель и знаменатель на tg(a/2) и заменим tga по формуле (119.9), тогда получим
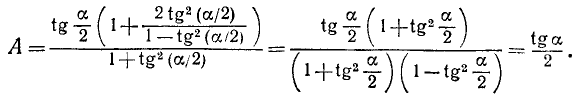
Пример:
Доказать, что
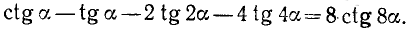
Решение:
Заметим, что
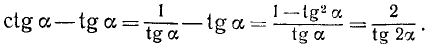
Преобразуя левую часть тем же способом и далее, получим последовательно
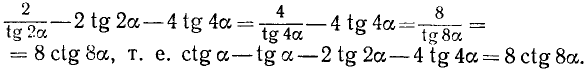
Тождество доказано.
Выражение через степени при натуральном числе
Выражение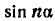 
и 
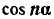через степен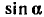и 
и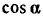 
при натуральном числе n.
Случай, когда n = 2, дан формулами (119.1), (119.2). Выразим теперь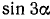 
, 
, 
, 
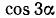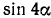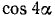и вообще 
, 
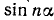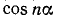через 
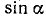и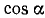 
. Укажем на два способа получения соответствующих формул. Покажем, например, как получаются формулы для 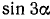и .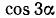
Первый способ. Представляем 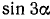в виде 
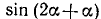и используем формулу (116.1), а затем используем формулы (119.1) и (119.2):
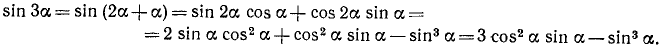
Итак,
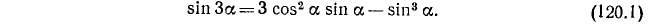
В правую часть формулы (120.1) входят sin а и cos а; заменив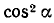 
на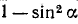 
, придем к следующей формуле:
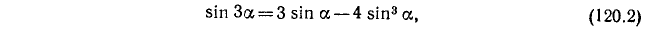
которая содержит в правой части только степени sin а. Аналогичные формулы можно получить для cos За:
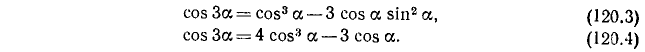
Заметим, что формулы (120.1) и (120.2) являются частным случаем формулы (118.1), когда в последней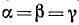 
. Формулы же (120.3) и (120.4) — частный случай формулы (118.2).
Второй способ. Воспользуемся результатами, полученными в алгебре при изучении комплексных чисел. На основании формулы Муавра (п. 17)
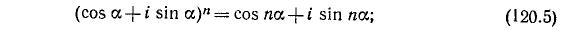
для случая, когда n = 3, имеем
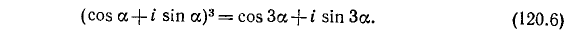
Два комплексных числа равны тогда и только тогда, когда равны соответственно их действительные и мнимые части. Теперь из равенства
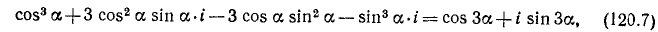
отделяя (и соответственно приравнивая) действительную и мнимую части, получим формулы
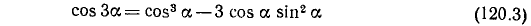
и
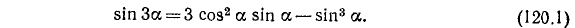
В общем случае для получения sin na и cos na можно поступать также двумя способами: либо применять последовательно теоремы сложения (первый способ), либо пользоваться формулой Муавра (второй способ).
Пример:
Упростить выражение
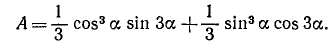
Решение:
Применив формулы (120.1) и (120.3), получим
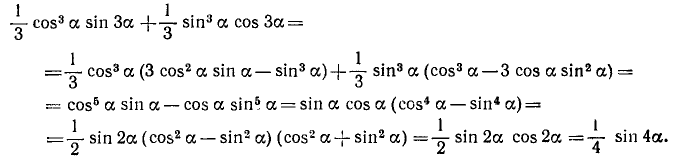
В конце решения примера мы воспользовались формулами (119.2), (99.1) и (119.1).
Тригонометрические функции половинного аргумента
Часто бывает необходимо, зная тригонометрические функции аргумента , найти тригонометрические функции аргумента 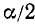. Выведем соответствующие формулы. Мы имеем
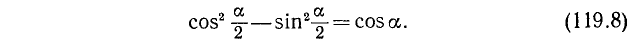
Присоединим к этой формуле основное тригонометрическое тождество:
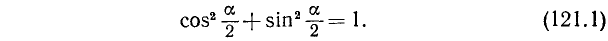
Сложив почленно (119.8) и (121.1), получим
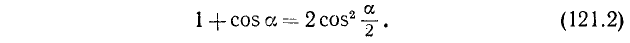
Вычитая (119.8) из (121.1), получим
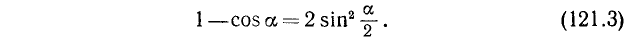
Из тождеств (121.2) и (121.3) соответственно имеем
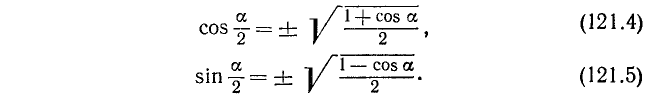
Разделив почленно тождество (121.3) на (121.2), приходим к тождеству
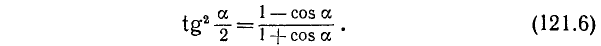
Из последнего тождества имеем
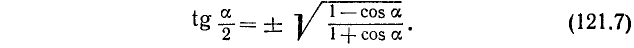
Применяя формулы (121.4), (121.5) и (121.7), следует всякий раз заботиться о знаке, который нужно взять перед радикалом.
Для вычисления tg (а/2) могут быть использованы и формулы, выражающие tg (a/2) через cos а и sin а рационально. Выведем эти формулы:
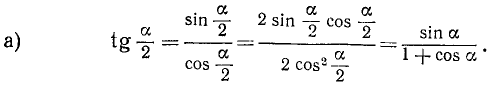
Итак,
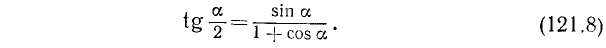
Так как всегда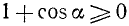 
(формула (121.8) имеет смысл только при 1 + cos a > 0), то из (121.8) можно заключить, что знак 
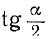во всех случаях совпадает со знаком sin а.
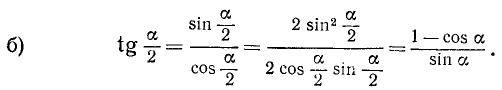
Итак,
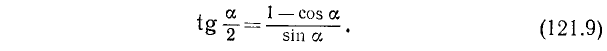
Из последней формулы также ясно, что знак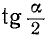 
совпадает со знаком sin а, ибо всегда 
.
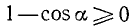Пример:
Найти sin 22°30′, cos 22°30 и tg 22°30 .
Решение:
Мы знаем, что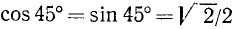 
. Следовательно, применяя формулы (121.5), (121.4) и (121.9), получим
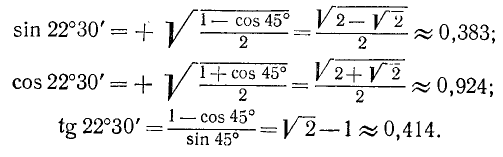
Пример:
Дано: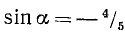 
, где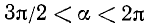 
. Найт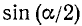и 
и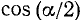 
.
Решение:
Сначала находим
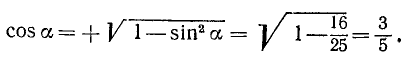
Так как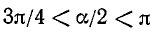 
, то 
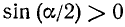, a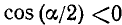 
.
Применяя формулы (121.5), (121.4) и беря в них радикалы с соответствующими знаками, получим
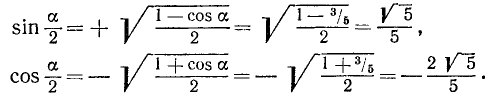
Пример:
Доказать тождество
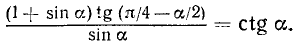
Решение:
Так как ctg а = cos a/sin а, то достаточно доказать, что
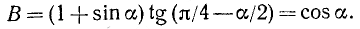
На основании формул приведения и (99.2) имеем
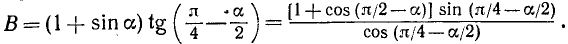
Применяя формулу (121.2), получим
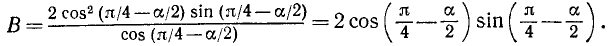
Далее получаем
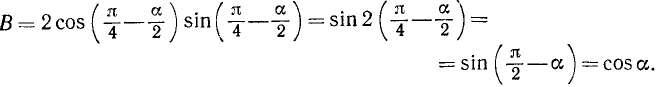
(Мы применили сначала формулу (119.1), приняв за данный аргумент 
, а за удвоенный аргумент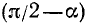 
, а затем формулу приведения (105.1).) Следовательно, тождество доказано.
Выражение основных тригонометрических функций аргумента a через tg (a/2)
Иногда требуется основные тригонометрические функции (sin a, cos a, tg a и ctg а) выразить рационально через tg (a/2). Покажем, например, как это делается для sin а. Используя тождества
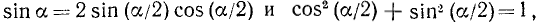
можно писать
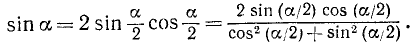
Разделив числитель и знаменатель дроби, стоящей в правой части последнего равенства, почленно на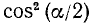 
, получим
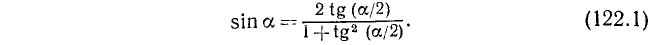
Используя тождество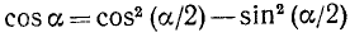 
, можно доказать, что
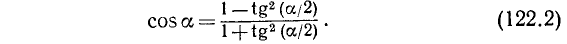
Соответствующая формула для tg a приводилась нами в п. 119:
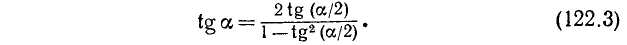
Зная tg a можно получить формулу
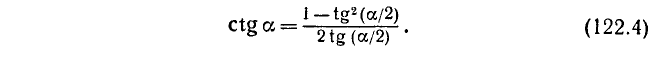
Замечание. Формулы (122.1)—(122.4) имеют смысл для всех значений аргумента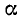 
, кроме 
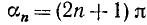, где n — целое число.
Пример:
Дано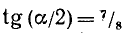 
. Найти sin a, cos a и tg a.
Решение:
На основании формулы (122.1) имеем
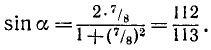
Аналогично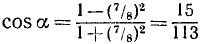 
. tg a уже проще искать так: 
.
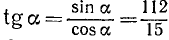Пример:
Вычислить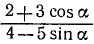 
, если 
.
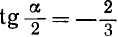Решение:
На основании формул (122.1) и (122.2) находим
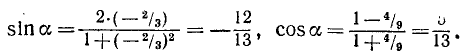
Далее,
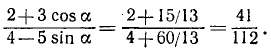
Преобразование в сумму выражений
Преобразование в сумму выражений вида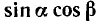 
, 
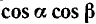и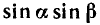 
Основные формулы. Вернемся к формулам (116.1) и (116.2):
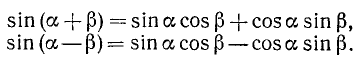
Сложив эти тождества почленно и разделив на 2, получим
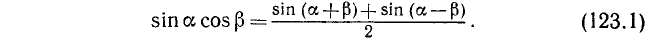
Выполнив аналогичные действия с формулами (115.3) и (115.4):
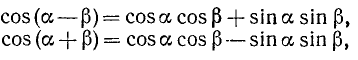
получим
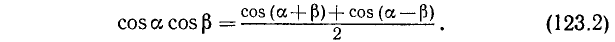
Вычтем из (115.3) почленно (115.4) и разделим на 2; получим
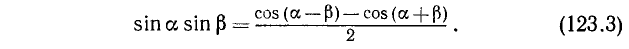
Примеры:
Иногда при решении примеров, имея произведения тригонометрических функций, например функций аргументов 
и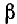 
, бывает полезно перейти к полусуммам или к полуразностям соответствующих тригонометрических функций.
Пример:
Упростить
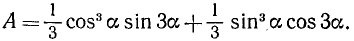
Решение:
Мы решали этот пример в п. 120, используя формулы (120.1) и (120.3) для sin 3a и cos 3a. Покажем теперь, как можно этот же пример решить, используя формулу (123.1). Заметим, что
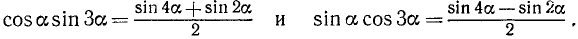
Используя только что полученные соотношения, будем иметь
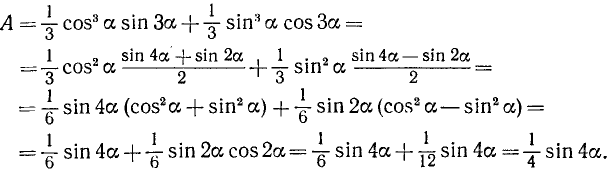
(В конце решения примера мы воспользовались формулами п. 119.)
Пример:
Упростить
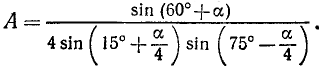
Решение:
Преобразовав произведение, стоящее в знаменателе, получаем
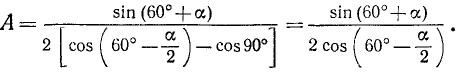
Знаменатель преобразуем при помощи формулы приведения
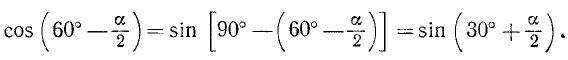
Числитель же преобразуем так:
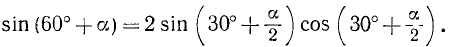
Тогда
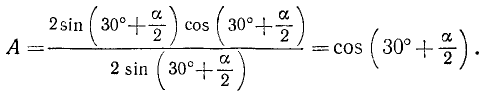
Пример:
Вычислить А = sin20°sin40°sin80°. Решение. Заметим, что
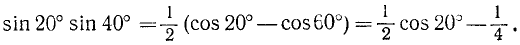
Далее,
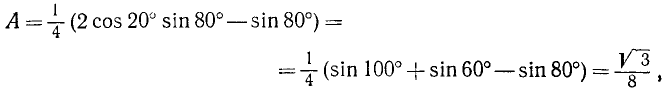
так как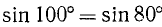 
, а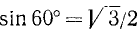 
.
Преобразование в произведение сумм
вида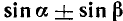 
, 
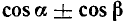и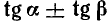 
125. Основные формулы. При вычислении различных выражений, содержащих тригонометрические функции, с помощью таблиц логарифмов и логарифмической линейки удобно иметь дело с произведениями, а не с суммами. Выведем ряд формул, которые позволяют от сумм переходить к произведениям.
а) Сумма синусов. Запишем формулу (123.1) в виде
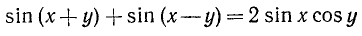
и положим в не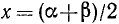й 
и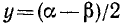 
. Заметим, что 
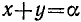и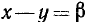 
; следовательно,
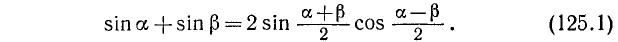
Сумма двух синусов равна удвоенному произведению синуса полусуммы на косинус полуразности их аргументов.
Пример:
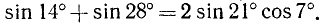
Пример:
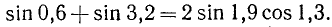
б) Разность синусов. Заменив в формуле (125.1)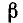 
на 
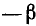, получим, учитывая нечетность синуса,
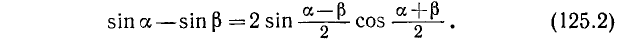
Разность двух синусов равна удвоенному произведению синуса полуразности на косинус полусуммы их аргументов.
Пример:
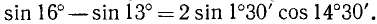
Пример:
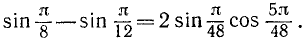
в) Сумма косинусов. Запишем формулу (123.2) в виде
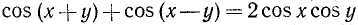
и положим в не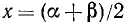й 
и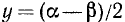 
. Мы уже видели, что 
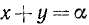и 
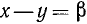; следовательно,
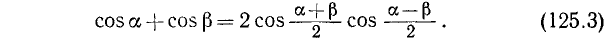
Сумма двух косинусов равна удвоенному произведению косинуса полусуммы на косинус полуразности их аргументов.
Пример:
cos 52°30′ + cos 16°30′ = 2 cos 34°30′ cos 18°.
Пример:
cos0,8 + cos2,8 — 2cos1,8cos1.
г) Разность косинусов. Из формулы (123.3), аналогично предыдущему, получается формула
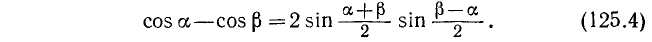
Разность двух косинусов равна удвоенному произведению синуса полусуммы на синус обратной полуразности их аргументов.
Пример:
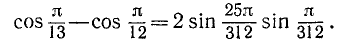
Пример:
cos 1,6 — cos 1,4 = —2 sin 1,5 sin 0,1.
д) Сумма тангенсов. Перейдя к синусам и косинусам, получим
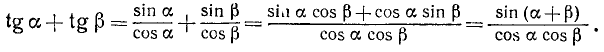
Итак,
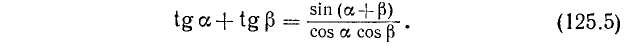
Пример:
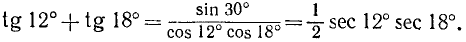
Пример:
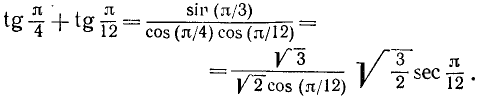
е) Разность тангенсов. Заменив в формуле (125.5) 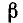на 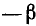, будем иметь, учтя четность косинуса и нечетность тангенса,
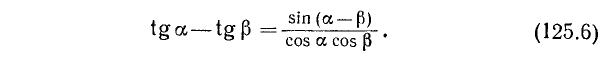
Пример:
Преобразовать по формуле (125.6) и вычислить, используя таблицу тригонометрических функций (приложение II),
tg 0,55 — tg 0,15.
Решение:
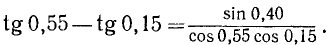
В нашей таблице нет значений функций для аргументов 0,55 и 0,15, поэтому, воспользовавшись формулой (123.2), перейдем к полусумме косинусов, но уже от аргументов, которые имеются в таблице:
Теперь имеем
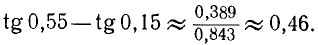
Пример:
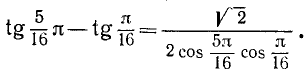
Замечание:
Последние две формулы (125.5) и (125.6) имеют смысл для аргументов и 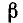, отличных от 
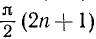, где n — целое число.
Примеры:
Пример:
Преобразовать в произведение выражение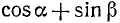 
.
Решение:
Заменив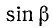 
по формуле приведения на 
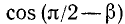, перейдем к сумме косинусов и воспользуемся формулой (125.3):
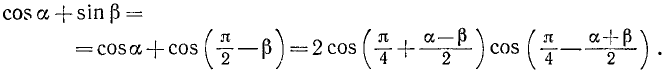
Пример:
Преобразовать в произведение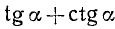 
.
Решение:
Перейдя к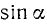 
и 
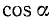, получим
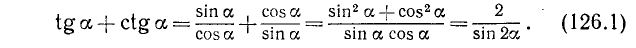
Пример:
Привести к виду, удобному для логарифмирования,
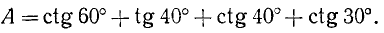
Peшeние:
Заменив ctg 60° по формуле приведения на tg 30° и воспользовавшись формулой (126.1), получим
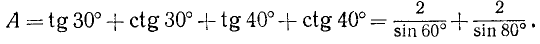
Далее, будем иметь
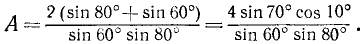
Последнее выражение можно упростить, если заметить, что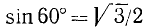 
, а sin 80° = cos 10°. Теперь будем иметь
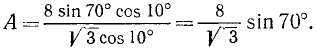
Пример:
Привести к виду, удобному; для логарифмирования,
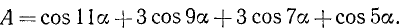
Решение:
Воспользовавшись формулой (125.3), получим
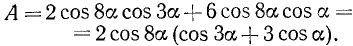
Согласно формуле (120.4)
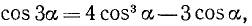
откуда
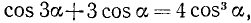
и мы имеем
Пример:
Доказать тождество
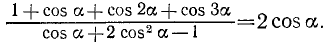
Решение:
Заметим, что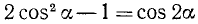 
(см. (121.2)) и 
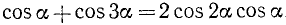. После этого преобразуем левую часть предполагаемого тождества:
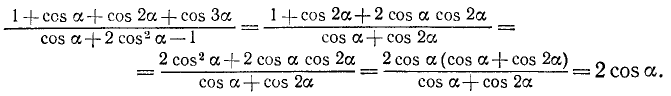
Следовательно, наше тождество доказано. Мы исключили из рассмотрения те значения аргумента а, при которых выражение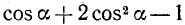 
или, что то же самое, 
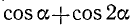равно нулю.
Пример:
Проверить, что tg 9°—tg 27° — tg 63° + tg 81° = 4.
Решение:
Заменив по формуле приведения tg 81° на ctg 9°, а tg 63° на ctg 27° и воспользовавшись формулой (126.1), получим
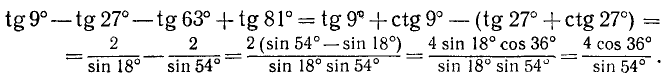
Заметив, что cos 36° = sin 54°, мы приходим к равенству 4 = 4. Итак, tg 9°—tg 27° — tg 63° + tg 81° = 4 .
Преобразование некоторых выражений в произведения с помощью введения вспомогательного аргумента
Некоторые суммы бывает возможно свести к произведениям, если соответствующим образом ввести вспомогательный аргумент. Проиллюстрируем этот прием на отдельных примерах.
Преобразование в произведение выражения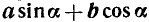 
. Мы предполагаем, что 
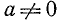и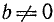 
. Постараемся подобрать аргумент 
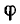и положительный множитель 
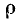так, чтобы было
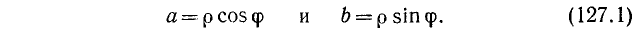
Возведя в квадрат обе части равенств (127.1) и сложив полученные равенства почленно, будем иметь
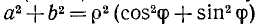
откуда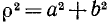 
и
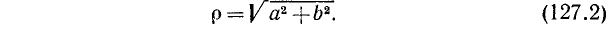
(В качестве 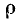мы берем арифметическое значение корня.) После этого вспомогательный аргумент 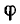можно найти из соотношений
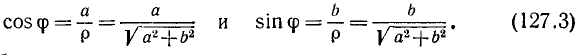
Теперь будем иметь
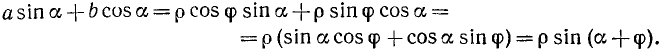
Итак,
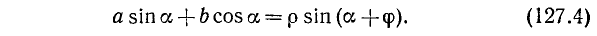
Формулу (127.4) можно получить и так:
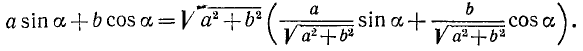
Положив теперь
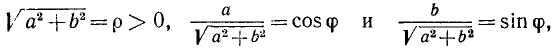
мы придем к формуле (127.4).
Замечание:
Тот факт, что такой аргумент 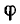существует, доказан в п. 100 
.
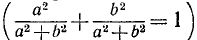Пример 1. Представить в виде произведения выражение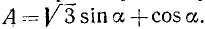 
.
Решение:
Здесь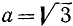 
, 
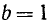и 
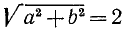. Следовательно,
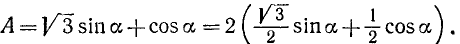
Теперь полагаем
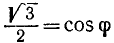и 
.
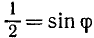В качестве аргумента 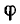можно взять, например, 
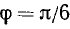. Окончательно имеем
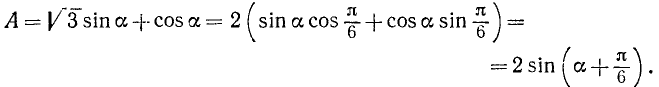
Пример:
Представить в виде произведения выражение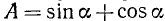 
.
Решение:
В этом примере а = 1 и b = 1, следовательно,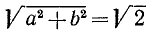 
. Теперь поступаем, как в общем случае:
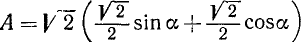
Положим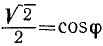 
и 
.
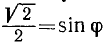В качестве аргумента 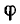можно взять, например, 
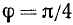. После этого получим
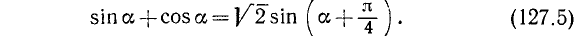
Преобразование в произведение выражений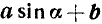 
и 
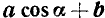при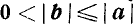 
.
1) Рассмотрим выражение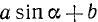 
. Запишем его следующим образом:
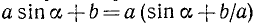
Так как, по предположению,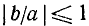 
, то можно положить 
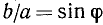. Теперь будем иметь
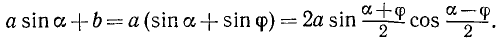
Пример:
Преобразовать в произведение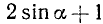 
.
Решение:
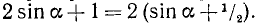
Положим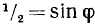 
. В качестве 
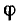можно, например, взять 
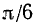, и мы получим
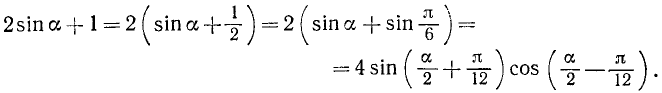
2) Рассмотрим выражение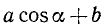 
. Запишем его следующим образом:
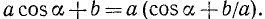
Так как, по предположению,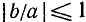 
, то можно положить 
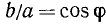. Теперь будем иметь
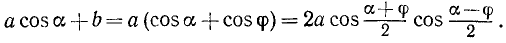
Пример:
Преобразовать в произведение
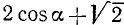
Решение:
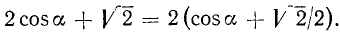
Положим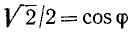 
. В качестве 
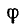можно, например, взять 
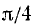, и мы получим
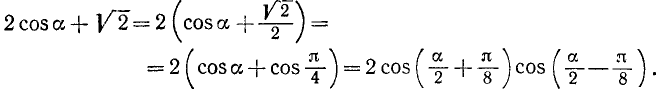
Пример:
Преобразовать в произведение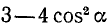 
. Решение.
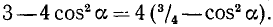
Положим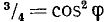 
. В качестве 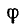можно, например, взять 
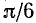, и мы будем иметь
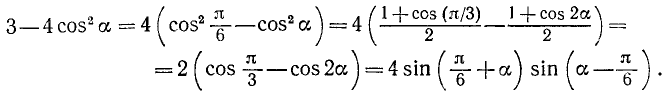
Преобразование в произведение выражения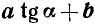 
. Рассмотрим выражение 
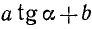, где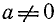 
. Запишем его следующим образом:
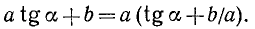
Так как тангенс изменяется в пределах от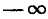 
до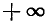 
, то при любых а и b можно положить 
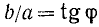, и мы получим
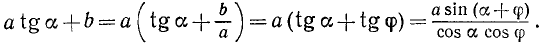
Пример:
Преобразовать в произведение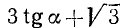 
. Решение.
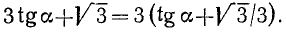
Положим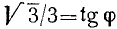 
. В качестве 
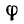можно, например, взять 
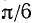, и мы будем иметь
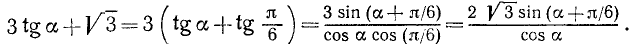
Пример:
Преобразовать в произведение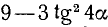 
. Решение.
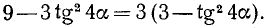
Положим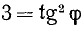 
. В качестве 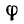можно, например, взять 
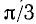, и мы получим
Решение заданий и задач по предметам:
Дополнительные лекции по высшей математике:
- Тождественные преобразования алгебраических выражений
- Функции и графики
- Преобразования графиков функций
- Квадратная функция и её графики
- Алгебраические неравенства
- Неравенства
- Неравенства с переменными
- Прогрессии в математике
- Арифметическая прогрессия
- Геометрическая прогрессия
- Показатели в математике
- Логарифмы в математике
- Исследование уравнений
- Уравнения высших степеней
- Уравнения высших степеней с одним неизвестным
- Комплексные числа
- Непрерывная дробь (цепная дробь)
- Алгебраические уравнения
- Неопределенные уравнения
- Соединения
- Бином Ньютона
- Число е
- Непрерывные дроби
- Функция
- Исследование функций
- Предел
- Интеграл
- Двойной интеграл
- Тройной интеграл
- Интегрирование
- Неопределённый интеграл
- Определенный интеграл
- Криволинейные интегралы
- Поверхностные интегралы
- Несобственные интегралы
- Кратные интегралы
- Интегралы, зависящие от параметра
- Квадратный трехчлен
- Производная
- Применение производной к исследованию функций
- Приложения производной
- Дифференциал функции
- Дифференцирование в математике
- Формулы и правила дифференцирования
- Дифференциальное исчисление
- Дифференциальные уравнения
- Дифференциальные уравнения первого порядка
- Дифференциальные уравнения высших порядков
- Дифференциальные уравнения в частных производных
- Тригонометрические функции
- Тригонометрические уравнения и неравенства
- Показательная функция
- Показательные уравнения
- Обобщенная степень
- Взаимно обратные функции
- Логарифмическая функция
- Уравнения и неравенства
- Положительные и отрицательные числа
- Алгебраические выражения
- Иррациональные алгебраические выражения
- Преобразование алгебраических выражений
- Преобразование дробных алгебраических выражений
- Разложение многочленов на множители
- Многочлены от одного переменного
- Алгебраические дроби
- Пропорции
- Уравнения
- Системы уравнений
- Системы уравнений высших степеней
- Системы алгебраических уравнений
- Системы линейных уравнений
- Системы дифференциальных уравнений
- Арифметический квадратный корень
- Квадратные и кубические корни
- Извлечение квадратного корня
- Рациональные числа
- Иррациональные числа
- Арифметический корень
- Квадратные уравнения
- Иррациональные уравнения
- Последовательность
- Ряды сходящиеся и расходящиеся
- Тригонометрические функции произвольного угла
- Тригонометрические формулы
- Обратные тригонометрические функции
- Теорема Безу
- Математическая индукция
- Показатель степени
- Показательные функции и логарифмы
- Множество
- Множество действительных чисел
- Числовые множества
- Преобразование рациональных выражений
- Преобразование иррациональных выражений
- Геометрия
- Действительные числа
- Степени и корни
- Степень с рациональным показателем
- Тригонометрические функции угла
- Тригонометрические функции числового аргумента
- Тригонометрические выражения и их преобразования
- Комбинаторика
- Вычислительная математика
- Прямая линия на плоскости и ее уравнения
- Прямая и плоскость
- Линии и уравнения
- Прямая линия
- Уравнения прямой и плоскости в пространстве
- Кривые второго порядка
- Кривые и поверхности второго порядка
- Числовые ряды
- Степенные ряды
- Ряды Фурье
- Преобразование Фурье
- Функциональные ряды
- Функции многих переменных
- Метод координат
- Гармонический анализ
- Вещественные числа
- Предел последовательности
- Аналитическая геометрия
- Аналитическая геометрия на плоскости
- Аналитическая геометрия в пространстве
- Функции одной переменной
- Высшая алгебра
- Векторная алгебра
- Векторный анализ
- Векторы
- Скалярное произведение векторов
- Векторное произведение векторов
- Смешанное произведение векторов
- Операции над векторами
- Непрерывность функций
- Предел и непрерывность функций нескольких переменных
- Предел и непрерывность функции одной переменной
- Производные и дифференциалы функции одной переменной
- Частные производные и дифференцируемость функций нескольких переменных
- Дифференциальное исчисление функции одной переменной
- Матрицы
- Линейные и евклидовы пространства
- Линейные отображения
- Дифференциальные теоремы о среднем
- Теория устойчивости дифференциальных уравнений
- Функции комплексного переменного
- Преобразование Лапласа
- Теории поля
- Операционное исчисление
- Системы координат
- Рациональная функция
- Интегральное исчисление
- Интегральное исчисление функций одной переменной
- Дифференциальное исчисление функций нескольких переменных
- Отношение в математике
- Математическая логика
- Графы в математике
- Линейные пространства
- Первообразная и неопределенный интеграл
- Линейная функция
- Выпуклые множества точек
- Система координат
