Оглавление:
Комбинаторика — это область математики, прежде всего связанная с подсчетом, как средство и цель получения результатов, так и с определением свойств конечных структур. Она тесно связана со многими другими областями математики — алгеброй, геометрией, теорией вероятностей и применяется в различных областях знаний (например, в генетике, информатике, статистической физике).
Комбинаторика (или комбинаторный анализ) — раздел математики, объектом исследования которого являются дискретные множества произвольной природы. Основной задачей комбинаторики является определение числа способов выполнения некоторых точно определенных операций, или, другими словами, определение числа подчиненных тем или иным условиям комбинаций, которые можно составить из заданной совокупности объектов.
Основные теоремы комбинаторики
Подмножества и выборки: Пусть задано произвольное множество из 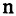 -объектов, которое мы обозначим за А, с элементами
-объектов, которое мы обозначим за А, с элементами 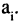 Последовательность произвольных элементов
Последовательность произвольных элементов
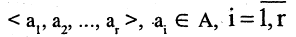
называется выборкой объема r из А, причем каждый элемент из множества А может встречаться в выборке произвольное число раз. Объем выборки может превосходить объем исходного множества А. Если же все компоненты r-выборки
из 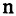 -множества А различны, то
-множества А различны, то 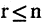 и r-выборка представляет cобой r-подмножество А. Выборки подразумевают возможность наличия в них одинаковых элементов, а подмножество не допускает повторений элементов. Для отличия подмножеств от выборок в формулах для выборок введем подчеркивание сверху.
и r-выборка представляет cобой r-подмножество А. Выборки подразумевают возможность наличия в них одинаковых элементов, а подмножество не допускает повторений элементов. Для отличия подмножеств от выборок в формулах для выборок введем подчеркивание сверху.
Если свойства выборки изменяются при транспозиции элементов (т.е. при перемене местами двух элементов), то выборка называется упорядоченной, в противном случае — неупорядоченной. Число появлений одного и того же элемента называется его кратностью и обозначается 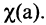 Типичным примером выборки может являться слово в фиксированном алфавите. Следовательно, если каждый элемент
Типичным примером выборки может являться слово в фиксированном алфавите. Следовательно, если каждый элемент 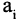 m-выборки Имеет кратность
m-выборки Имеет кратность 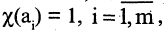 то выборка является просто m-подмножеством множества А. Упорядоченное m-подмножество n-множества называется m-перестановкой из n-элементов (или размещением из n-элементов по m).
то выборка является просто m-подмножеством множества А. Упорядоченное m-подмножество n-множества называется m-перестановкой из n-элементов (или размещением из n-элементов по m).
Неупорядоченное m-подмножество n-множества называется m-сочетанием из m-элементов (или сочетанием из n-элементов по m). Число 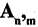 упорядоченных m-подмножеств n-множества равно
упорядоченных m-подмножеств n-множества равно
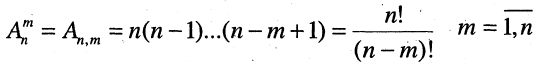
Если 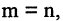 то число таких подмножеств есть
то число таких подмножеств есть
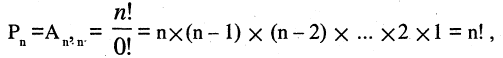
т. е. равно произведению всех первых n- натуральных чисел, так как по определению 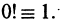
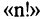 читается: «n — факториал». Размещения из n элементов по n называются просто перестановками. Чтобы показать очень быстрый рост числа перестановок с ростом числа n, сравним числа
читается: «n — факториал». Размещения из n элементов по n называются просто перестановками. Чтобы показать очень быстрый рост числа перестановок с ростом числа n, сравним числа 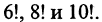 Вычисляя, получим:
Вычисляя, получим: 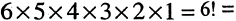
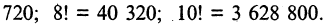 Величина
Величина 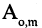 принимается равной единице, хотя она и не имеет комбинаторного смысла. Кроме того, по определению
принимается равной единице, хотя она и не имеет комбинаторного смысла. Кроме того, по определению 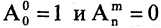 при значениях
при значениях 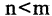 или если
или если 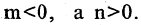 Имеет место рекуррентное (возвратное) соотношение
Имеет место рекуррентное (возвратное) соотношение
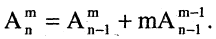
Подсчет 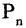 при больших значениях n становится затруднительным. В этих случаях можно рекомендовать) использовать приближенную формулу Стирлинга:
при больших значениях n становится затруднительным. В этих случаях можно рекомендовать) использовать приближенную формулу Стирлинга:
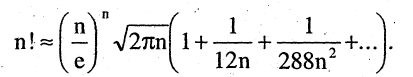
Пример:
Сколько вариантов расположения слов допускает предложение: «Редактор вчера внимательно прочитал рукопись»? Так как в данном предложении нет никаких грамматических ограничений на порядок слов, то на первое место можно поставить любое слово (5 вариантов), на второе -любое другое, кроме выбранного (4 варианта) и т. д.; всего 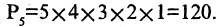
Если рассматривается произведение первых натуральных только четных или только нечетных чисел, то такие произведения называются двойными факториалами и обозначаются так:
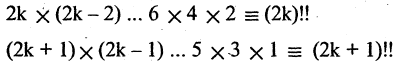
Число 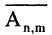 упорядоченных m-выборок из n-множеств равно
упорядоченных m-выборок из n-множеств равно
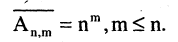
Пример:
Сколько всего телефонных номеров можно иметь в городе, если номер имеет шесть цифр? Решение. Каждый телефонный номер может содержать любые шесть цифр из десяти (0, 1, 2, …, 9). При этом одинаковые цифры могут повторяться до шести раз, и, кроме того, телефонные номера различны, даже если они отличаются лишь порядком цифр. На основании этого задача сводится к подсчету количества 6-выборок 10-множества, т. е. 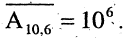
Число 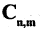 неупорядоченных m-подмножеств n-множества (число сочетаний) равно
неупорядоченных m-подмножеств n-множества (число сочетаний) равно
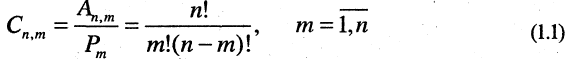
Сочетания — это соединения из n-элементов по m-элементов, которые отличаются друг от друга только самими элементами. Числа 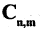 обычно называют биномиальными коэффициентами. Если в этой формуле заменить m на разность n — m, то получим »отношение
обычно называют биномиальными коэффициентами. Если в этой формуле заменить m на разность n — m, то получим »отношение
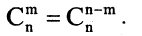
Рекуррентная формула для сочетаний 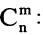
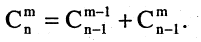
Принято считать, что 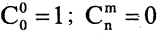 при
при 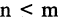 или при
или при 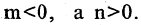
Числа 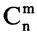 часто условно записывают в следующем виде:
часто условно записывают в следующем виде: 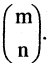
Хотя величина 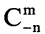 не имеет комбинаторного смысла, понятие чисел
не имеет комбинаторного смысла, понятие чисел 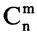 можно распространить на отрицательные значения n, а именно:
можно распространить на отрицательные значения n, а именно:
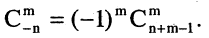
Пример:
Абонент забыл последние три цифры телефонного номера. Какое наибольшее число вариантов номеров ему нужно перебрать, чтобы дозвониться (в этом случае необходимый номер набирается последним)? Очевидно, что таких номеров столько, сколько можно составить размещений из десяти цифр
по три, т. е. 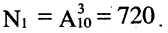
Пример:
Требуется составить колонну из пяти автомашин. Сколькими способами это можно сделать? По условиям задачи порядок следования автомобилей может быть любым, поэтому количество способов составить автоколонну из пяти машин есть число перестановок из пяти: 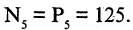
Пример:
Читатель отобрал по каталогу 8 книг. Однако в библиотеке выдают одному читателю не более 5 книг. Сколько альтернатив взять книги есть у этого читателя? Решение. Поскольку читатель отобрал книг больше разрешенного числа, то он должен выбрать из них 5 книг. Естественно, что все книги, разные и все равно, в каком порядке их взять. Следовательно, каждая альтернатива есть неупорядоченное 5 — подмножество из 8 и число вариантов в выборе книг (число альтернатив) равно
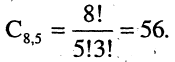
Число 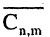 неупорядоченных m-выборок из n-множества равно
неупорядоченных m-выборок из n-множества равно
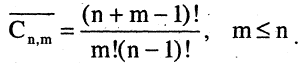
Пример:
Кости домино можно рассматривать как сочетания с повторениями по два из семи цифр: 0,1,2,3,4, 5,6. Число всех таких сочетаний равно
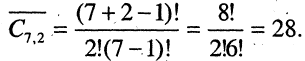
Набор целых чисел 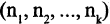 называется разбиением числа n, если
называется разбиением числа n, если 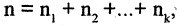 например 6=1+2+3.
например 6=1+2+3.
Число разбиений. Число R 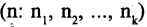 упорядоченных
упорядоченных 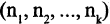 — разбиений n-множества равно.
— разбиений n-множества равно.
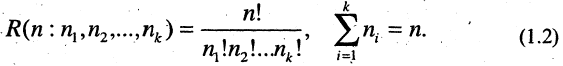
Замечание:
Числа R в (2.4) называют также полиномиальными коэффициентами. Это название обусловлено тем, что они являются коэффициентами при произведениях степеней переменных 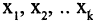 в разложении полинома по степеням
в разложении полинома по степеням 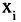
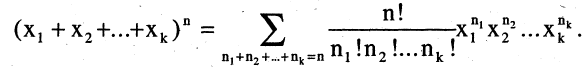
В частном случае, когда  имеем соотношение
имеем соотношение
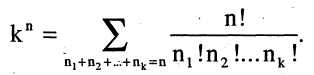
Число (m, n — m) — разбиений n-множества равно числу его упорядоченных m-подмножеств.
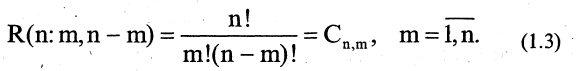
Пример:
Число различных слов, которое получим, переставляя буквы слова «математика», равно
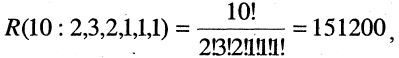
так как кратность букв м равна двум, а — трем, т- двум, остальные буквы встречаются по одному разу.
Число неупорядоченных подмножеств. Число 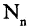 всех неупорядоченных подмножеств n-множества равно
всех неупорядоченных подмножеств n-множества равно 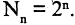
Пример:
В комнате 4 различных светильника. Сколько вариантов включения светильников может быть реализовано?
Так как в задаче речь идет лишь о том, горит светильник или нет, то мы рассматриваем неупорядоченные разбиения, т. е. применима формула 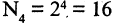 (вариантов).
(вариантов).
Основные правила комбинаторики
Комбинаторика – раздел математики, который изучает задачи выбора и расположения элементов из некоторого основного множества в соответствии с заданными правилами.
Правило суммы
Пусть существует разбиение множества изучаемых комбинаций на классы, т. е. каждая комбинация входит в один и только в один класс. Тогда полное число комбинаций равно сумме количества комбинаций, входящих в каждый из классов. Иными словами, если некоторый объект типа а можно выбрать m-способами, а объект типа b можно выбрать n-способами, то выбор одного из этих объектов можно осуществить 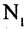 — способами:
— способами:

Это правило сумм справедливо лишь в том случае, если классы разбиения не пересекаются. Если же классы разбиения пересекаются, т. е. способы выбора объекта типа а совпадают со способами выбора объекта типа b, то из формулы (1.4) следует вычесть число k таких совпадений:

Пример:
Пусть а — число, делящееся на два; b — число, делящееся на три. Сколькими способами можно выбрать или а, или b, если задано множество 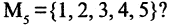 Решение. Согласно формуле (1.4), имеем:
Решение. Согласно формуле (1.4), имеем: 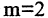 (числа 2 и 4) и
(числа 2 и 4) и 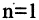 (число 3), т. е.
(число 3), т. е. 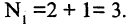
Если подобный выбор осуществляется из множества 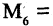
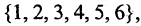 то необходимо использовать уже формулу (1.5), т.к. 6 делится и на 2 и на 3:
то необходимо использовать уже формулу (1.5), т.к. 6 делится и на 2 и на 3: 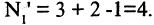
Обобщая формулы на случай i классов, получим формулу сумм
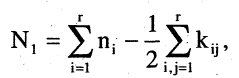
где 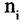 — число способов выбора объектов i-го типа;
— число способов выбора объектов i-го типа; 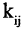 — число совпадений способов выбора объектов i-го и j-го типа.
— число совпадений способов выбора объектов i-го и j-го типа.
Правило произведения
Если объект типа а можно выбрать m способами и если после каждого такого выбора объект типа b можно выбрать n способами, то выбор в указанном порядке пары 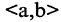 можно осуществить
можно осуществить 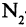 -способами:
-способами: 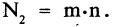
Если же при i-м способе выбора объекта типа а объект b может быть выбран 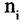 -способами, то число
-способами, то число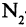 способов такого выбора пары
способов такого выбора пары 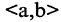 равно
равно
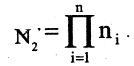
Пример:
Сколько существует целых четырехзначных чисел, не делящихся на 5? Целое число не делится на 5, если оно не заканчивается на 5 или на 0. Поэтому первую значащую цифру можно выбирать девятью способами (все цифры, кроме нуля), вторую и третью — десятью способами, а четвертую лишь восемью (все цифры, кроме 0 и 5). Следовательно, искомое число есть
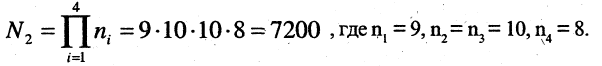
Комбинации объектов
Размещения с повторениями — это упорядоченные m-выборки из n-множества. Таких выборок будет 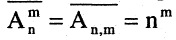 штук.
штук.
Перестановки с повторениями — это упорядоченные разбиения п-множества  , т. е. мы имеем
, т. е. мы имеем
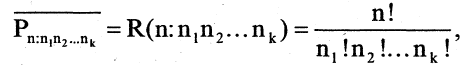
где 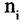 — число повторений в перестановке элементов i-го типа.
— число повторений в перестановке элементов i-го типа.
Очевидно, что
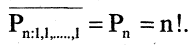
Пример:
Сколько различных слов можно составить, переставляя буквы в слове «перепел»?
Решение:
Поскольку в слове имеются три буквы е и две буквы п, перестановки будут происходить с повторениями.
Поэтому искомое число есть
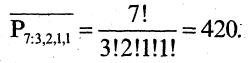
Сочетания с повторениями — это неупорядоченные m-выборки из n-множества. Поэтому число таких сочетаний, согласно теореме о числе неупорядоченных выборок, равно
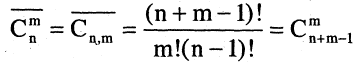
Имеет место также следующее рекуррентное соотношение:
Пример:
Число целых неотрицательных решений уравнениях, 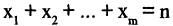 равно числу сочетаний из m-элементов по n-элементов с повторениями. Это, в частности, означает, что уравнение
равно числу сочетаний из m-элементов по n-элементов с повторениями. Это, в частности, означает, что уравнение 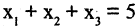 имеет
имеет 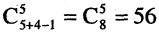 решений.
решений.
Комбинаторные задачи
Среди различных задач, которые приходится решать математикам, встречаются такие, где нужно ответить на вопрос: каким числом различных способов можно осуществить требуемое? Такие задачи принято называть комбинаторными задачами. Для решения таких задач созданы общие методы и выведены готовые формулы. Однако для того чтобы лучше ознакомиться с методами их решения, мы начнем не с общих методов и готовых формул, а с рассмотрения конкретных примеров.
Пример:
Каким числом способов можно обить 12 раз личных стульев, если есть 12 образцов обивочного материала, причем каждый материал имеется в любом количестве?
Решение:
Поскольку имеется 12 различных образцов обивочного материала, то один стул можно обить двенадцатью различными способами. То же самое справедливо и для второго стула, так как каждый обивочный материал имеется в любом количестве. Но каждый способ обивки первого стула можно соединить с любым способом обивки второго, так что число различных способов обивки двух стульев равно 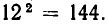
При этом важно, что имеющиеся стулья различны. Если бы они были одинаковыми, то число различных способов обивки было бы меньшим, так как способы, при которых первый стул обит матералом а, а второй — материалом b, или, наоборот, первый стул обит материалом b, а второй—материалом а, нельзя было бы считать различными способами.
Итак, для двух различных стульев мы получили 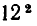 различных способов их обивки. Очевидно, что для каждого следующего стула остается в силе приведенное выше рассуждение: для каждого стула существует двенадцать возможных способов обивки, и каждый способ обивки данного стула можно соединить с любым способом обивки предыдущих. Отсюда следует, что для трех стульев число различных способов обивки составляет
различных способов их обивки. Очевидно, что для каждого следующего стула остается в силе приведенное выше рассуждение: для каждого стула существует двенадцать возможных способов обивки, и каждый способ обивки данного стула можно соединить с любым способом обивки предыдущих. Отсюда следует, что для трех стульев число различных способов обивки составляет 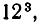 для четырех —
для четырех — 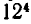 и т. д. Для двенадцати стульев это число составляет
и т. д. Для двенадцати стульев это число составляет 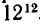
Пример:
Каким числом способов можно рассадить 12 гостей на имеющихся 12 различных стульях?
Решение:
Представим себе, что гости входят в комнату по одному. Первому из входящих гостей предоставляется выбор из 12 различных стульев, т. е. 12 возможностей, как и в предыдущем примере. Однако уже для следующего гостя остаются не те же две надцать возможностей, что и для первого, а всего лишь одиннадцать, поскольку один из стульев оказывается уже занятым. По-прежнему каждое место, занятое первым гостем, может комбинироваться с любым другим местом, занятым вторым; поэтому общее число различных способов, с помощью которых можно рассадить двух гостей, равно 12 • 11 = 132.
Дальнейший ход решения теперь уже ясен. Для гостя, входящего третьим, останется только 10 различных возможностей, так как из 12 мест два места окажутся уже занятыми. Поэтому для трех гостей число различных способов рассадить их составляет 12 • 11 • 10 = 1320. Продолжая аналогичные рассуждения, найдем, что общее число различных способов рассадить 12 гостей на 12 стульях составляет 12 • 11 • … • 2 • 1 = 12!= 479001600.
Пример:
В отделении 12 солдат. Каким числом способов можно составить наряд из двух человек, если один из них должен быть назначен старшим?
Решение этой задачи очень похоже на решение предыдущей. Действительно, если назначить сначала старшего по наряду, то для его выбора у нас имеется 12 различных возможностей: каждый солдат отделения может быть назначен старшим наряда. После того как старший наряда назначен, вторым в наряд может быть назначен любой из оставшихся одиннадцати. Как и во всех предыдущих случаях, общее число различных нарядов составляет 12- И = 132.
Пример:
Какое число различных парных нарядов можно назначить из 12 солдат отделения, если не требуется назначать старшего по наряду?
Решение:
Легко понять, что число таких нарядов должно быть меньше, чем в предыдущем примере. Действительно, наряды —Иванов (старший) и Петров или Петров (старший) и Иванов — различны, тогда как, если не требуется назначать старшего, эти два солдата в обоих случаях составляют один и тот же наряд. Каждый парный наряд без старшего можно превратить в два различных наряда со старшим. Поэтому число различных парных нарядов со старшим в два раза больше, чем нарядов без старших. Отсюда следует, что интересующее нас в данном примере число различных парных нарядов из 12 солдат отделения в два раза меньше, чем получено в предыдущем примере, т. е. равно 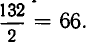
Пример:
Клавиатура пианино состоит из 88 клавиш. Сколько различных музыкальных фраз можно составить из 6 нот, допуская повторения одних и тех же нот в одной фразе?
Решение:
Как и в примере 1, в качестве первой ноты для музыкальной фразы можно взять любую из 88 нот, т. е. для первой ноты мы имеем 88 возможностей. Так как повторения допускаются, то для второй ноты мы снова имеем те же 88 возможностей, и поэтому музыкальных фраз из двух нот существует 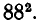 Продолжая рассуждения, как в примере 1, найдем, что число различных музыкальных фраз из 6 нот составляет
Продолжая рассуждения, как в примере 1, найдем, что число различных музыкальных фраз из 6 нот составляет 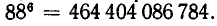
Пример:
Сколько различных музыкальных фраз можно составить из 6 нот, если не допускать в одной фразе повторений уже встречавшихся звуков?
Решение этой задачи так же отличается от решения предыдущей, как решение задачи примера 2 от примера 1. Действительно, при составлении произвольной музыкальной фразы для первой ноты мы имеем по-прежнему 88 возможностей. Для второй ноты число возможностей уменьшится уже до 87, так как нота, использованная первой, не должна больше употребляться. После того как выбрана вторая нота, для третьей остается уже только 86 возможностей. Теперь ясно, что общее число различных музыкальных фраз из 6 нот без повторений равно произведению 88 • 87 • 86 • 85 • 84 • 83 = 390 190489920.
Пример:
Сколько существует различных аккордов из шести нот?
Решение:
Аккорд отличается от музыкальной фразы тем, что все ноты, в него входящие, звучат одновременно. Отсюда следует, что все ноты аккорда должны быть различными. Кроме того, различные музыкальные фразы могут приводить к одному и тому же аккорду, если они состоят из одних и тех же нот, но расположенных в фразе в различном порядке. Поэтому, подобно примеру 4, так как число различных музыкальных фраз уже известно, нам остается определить, сколько различных музыкальных фраз могут «склеиваться» в один и тот же аккорд, или, наоборот, сколько различных фраз получается из одного и того же аккорда.
Мы приходим, таким образом, к задаче, аналогичной рассмотренной в примере 6: имеется аккорд из шести различных нот, сколько различных музыкальных фраз можно из него составить? В качестве первой ноты для составляемой музыкальной фразы можно взять любую из входящих в аккорд нот, то есть мы имеем для нее шесть различных возможностей. Для второй ноты остается уже только пять возможностей, для третьей — четыре и т. д.
Теперь уже ясно, что число различных музыкальных фраз, которые можно получить из одного аккорда из шести нот, равно 6 • 5 • 4 • 3 • 2 • 1 =6!= 720. Это означает, что 6! различных музыкальных фраз склеиваются в один и тот же аккорд, так что число возможных аккордов будет в 61 раз меньше, чем число различных музыкальных фраз. Итак, мы получаем, что число различных возможных аккордов из 6 нот равно:
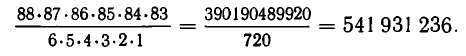
Пример:
Из города А в город В ведет k дорог, а в город С — l дорог. В город D из города В ведет m дорог, а из города С — n дорог. Города В и С дорогами не соединяются. Сколько различных автобусных маршрутов можно провести между городами А и D?
Решение:
Число автобусных маршрутов определяется числом различных дорог между городами. Всего из города А выходит k + l дорог, а в город D входит m + n дорог. Мы не можем, однако, сказать, что общее число дорог равно произведению этих чисел, так как здесь невозможно комбинировать любую дорогу, выходящую из A, с любой дорогой, входящей в D . Если же рассматривать отдельно дороги, проходящие через В или через С, то такая комбинация возможна.
Рассмотрим всевозможные маршруты, идущие из A в D через В. Из A в В ведет k дорог, а из В в D —m дорог. Каждую из таких дорог, выходящих из A, можно комбинировать с любой дорогой,, входящей в D поэтому общее число различных маршрутов, как и во всех предыдущих задачах, получается перемножением числа возможностей и равно km, Следовательно, число различных маршрутов, идущих из A в D через В, равно km.
Аналогично подсчитывается число различных маршрутов, идущих из A в D через С; оно равно ln. Далее, мы замечаем, что всякий автобусный маршрут, соединяющий города A и D, должен проходить или через В, или через С, и, значит, он должен входить либо в число km маршрутов, идущих через В, либо в число ln маршрутов, идущих через С. Общее число различных маршрутов равнo тогда сумме km + ln.
Прежде чем перейти к следующим примерам, подведем некоторые итоги. Рассмотренные в предыдущем параграфе примеры имели между собой много общего и решались по существу одинаковыми приемами. Главная мысль, которая лежит в основе всех решений, может быть сформулирована в виде следующего общего правила: если некоторый выбор может быть сделан т различными способами, а для каждого из этих способов некоторый второй выбор может быть сделан п различными способами, то число способов для осуществления последовательности двух этих выборов равно произведению mn.
Фактически при решении всех задач мы пользовались этим общим правилом, и нужно было только определить число различных возможностей в том или ином случае. Это число менялось в зависимости от условий задачи.
Другое общее правило имеет следующий вид: если некоторый выбор может быть сделан т различными способами, а другой выбор—n различными способами {отличными от предыдущих), то общее число способов, которыми можно осуществить какой-нибудь один из этих выборов, равен сумме m +n.
Это правило также применялось нами в предыдущем параграфе (см. пример 8).
При внимательном рассмотрении задач предыдущего параграфа можно заметить, что мы имеем дело с очень небольшим числом различных типов задач. Чтобы сделать этот вывод более наглядным, рассмотрим еще несколько примеров.
Пример:
Во взводе 5 сержантов и 50 солдат. Сколькими способами можно составить наряд из одного сержанта и трех солдат?
Решение:
Очевидно, что одного сержанта из пяти можно выбрать пятью различными способами. В соответствии с приведенным выше правилом остается определить число возможностей выбора трех солдат, а затем числа возможностей выбора солдат и выбора сержантов между собой перемножить, поскольку каждого сержанта можно отправить в наряд с любой группой солдат.
Для определения числа возможностей выбора трех солдат нам придется снова воспользоваться первым правилом, как мы это уже и делали все время, не формулируя его явно. Нам придется при этом действовать в два приема.
Представим себе сначала, что назначаемых в наряд солдат мы вызываем по одному и строим в шеренгу. Тогда легко подсчитать, что при вызове первого солдата у нас есть 50 различных возможностей; после того как один солдат уже вызван, для выбора второго остается 49 возможностей, а для выбора третьего — лишь 48. Таким образом, применяя правило умножения, находим, что всего для выбора трех солдат в определенном порядке число возможностей равно произведению 50 • 49 • 48. На этом и заканчивается первая часть решения, но отнюдь не все решение.
В предыдущем абзаце совсем не зря выделены слова «в определенном порядке». Полученное произведение не равно числу возможностей выбора трех солдат, а больше этого числа, причем выделенные слова как раз и объясняют, почему. Дело в том, что мы можем получить один и тот же наряд, вызывая солдате различном порядке. Поэтому необходимо подсчитать, какое число раз может получиться один и тот же наряд, и разделить полученное выше произведение на это число.
Остается, следовательно, определить, в каком числе случаев будет получаться один и тот же наряд. Это можно подсчитать, решая в каком-то смысле обратную задачу: каким числом способов можно расставить в шеренгу трех солдат уже выбранного наряда. Очевидно, что это число равно требуемому. Но это число легко под считать, пользуясь обычным приемом: чтобы поставить какого-либо солдата на первое место, есть три различные возможности, на второе место остается два солдата и на третье — только один Поэтому общее число возможных перестановок трех солдат в шеренге равно 3 • 2 • 1 = 3! = 6.
Итак, каждый наряд из трех солдат можно расставить в шеренгу 3! различными способами, а, значит, в произведении 50 • 49 • 48, показывающем число возможностей при выборе трех человек в определенном порядке, каждый наряд считается ровно 3! раз. Поэтому общее число различных способов, которыми можно назначить в наряд трех солдат из пятидесяти, равно
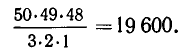
Число различных нарядов из одного сержанта и трех солдат равно теперь
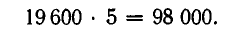
Пример:
Сколько членов, содержащих две буквы, получится после раскрытия скобок в выражении
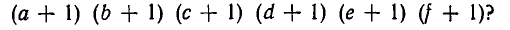
Решение:
После раскрытия всех скобок мы получим сумму некоторого числа слагаемых (нетрудно подсчитать, что общее число слагаемых равно 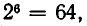 но для решения поставленной задачи это не существенно), каждое из которых состоит из шести множителей. Различные множители, входящие в одно и то же произведение, берутся из различных скобок. При этом для каждого множителя есть две различные возможности — он может быть либо буквой, либо единицей.
но для решения поставленной задачи это не существенно), каждое из которых состоит из шести множителей. Различные множители, входящие в одно и то же произведение, берутся из различных скобок. При этом для каждого множителя есть две различные возможности — он может быть либо буквой, либо единицей.
Вопрос, поставленный в условии, состоит в том, чтобы определить, каким числом способов можно из шести множителей выбрать две буквы. В такой постановке он решается уже совсем просто. Пользуясь уже часто употреблявшимися рассуждениями, мы можем сразу написать, что число различных слагаемых, содержащих две буквы, равно
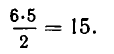
Действительно, для выбора первой буквы у нас есть шесть возможностей, а для выбора второй — пять. Кроме того, каждую пару букв мы считаем дважды, один раз полагая первой одну из них, а другой раз — вторую.
Пример:
Подсчитаем, сколько в рассмотренном в предыдущем примере произведении слагаемых, содержащих четыре буквы.
Решение этой задачи аналогично решению предыдущей. Тем же методом можно подсчитать, что выбор четырех букв в определенном порядке может быть сделан 6 • 5 • 4 • 3 = 360 различными способами. С другой стороны, каждая четверка считается здесь несколько раз, именно столько, каким числом способов можно ее упорядочить. Число способов упорядочить четверку букв равно произведению 4 • 3 • 2 • 1 = 24. Поэтому число слагаемых, содержащих четыре буквы, равно
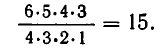
Этот ответ совпадает с ответом, полученным в предыдущем примере. Про это можно было бы догадаться заранее и, следовательно, обойтись без всяких вычислений, сославшись на предыдущий результат. В самом деле, легко понять, что комбинаций пар букв столько же, сколько комбинаций четверок: каждой паре букв соответствует одна-единственная определенная четверка, которая остается, когда мы удалим выбранную пару. Разным парам соответствуют разные четверки и, наоборот, разным четверкам соответствуют разные пары. Поэтому число различных пар и различных четверок букв одинаково.
Пример:
В классе m мест. Каким числом способов можно рассадить в нем n учеников (n < m)?
Решение:
Если в этой задаче и есть что-либо новое по сравнению с предыдущими, то только то, что в ней нет конкретных числовых данных. Способ решения задачи от этого, естественно, не изменяется.
Представим себе, что ученики входят в класс по одному. Тогда для первого из них имеется m возможностей выбрать место. После того как первый выбрал какое-то место, для второго остается m — 1 возможностей. Далее, для третьего будет m — 2 различных возможностей и т. д. Искомое число способов рассадить всех учеников выразится произведением
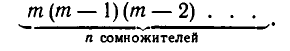
Найдем последний сомножитель этого произведения. Его можно определить по-разному, например так: каждый сомножитель на единицу меньше предыдущего и получается вычитанием из m числа, на единицу меньшего, чем номер сомножителя. Поэтому сомножитель с номером п получается вычитанием из т числа n — 1, то есть равен m — (n — 1) = m — n + 1.
Можно рассуждать и иначе: после того как все ученики рассядутся, в классе должно остаться m — n свободных мест. Перед входом последнего ученика свободных мест было на 1 больше, то есть m — n + 1. Таково же число возможностей для выбора мест последним учеником, то есть последний сомножитель в произведении.
Итак, искомое число различных способов рассадить n учеников на m местах равно произведению п последовательных целых чисел от m до m — n + 1 включительно:

Пример:
В комнате имеется пять лампочек. Сколько существует различных способов освещения?
Решение:
После всех рассмотренных примеров читатель уже самостоятельно справится с несложным подсчетом того, сколько существует способов освещения, при которых горит данное число лампочек. Сложив все полученные результаты для каждого числа лампочек (от нуля до пяти включительно), мы и получим ответ на поставленный вопрос. Однако этот способ решения, при всей своей простоте, потребует сравнительно длинных рассуждений и вычислений.
Между тем задача допускает простое и короткое решение, если проводить рассуждение в другом порядке. Рассмотрим сначала случай, когда в комнате имеется всего лишь одна лампочка. Тогда, очевидно, возможны ровно два различных способа освещения: лампочка либо горит, либо не горит.
Теперь присоединим к первой лампочке вторую. Она тоже может находиться в одном из двух состояний: гореть, либо не гореть. Так как каждое состояние второй лампочки можно комбинировать с любым состоянием первой, то для двух лампочек число различных состояний, то есть различных способов освещения, равно 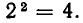
Дальнейшие рассуждения теперь уже совершенно очевидны. Каждая из лампочек может находиться в двух состояниях. Поэтому, присоединяя новую лампочку к уже рассмотренным предыдущим, мы увеличиваем число возможных способов освещения вдвое. Следовательно, при трех лампочках будет 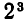 различных способов освещения, при четырех —
различных способов освещения, при четырех —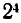 и, наконец, при пяти лампочках
и, наконец, при пяти лампочках 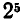 = 32 способа освещения.
= 32 способа освещения.
Пример:
Чему равен коэффициент при 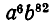 и при
и при 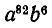 в выражении
в выражении 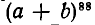 после раскрытия скобок.
после раскрытия скобок.
Решение:
Внимательный читатель сразу заметит, что этот пример очень похож на только что разобранный выше пример 4. Еще большую похвалу заслужит тот, кто заметит связь этого примера с примером 7 из предыдущего параграфа.
Выражение 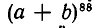 можно рассматривать как произведение 88 скобок; из каждой нужно выбрать в качестве множителя одно из слагаемых: либо а, либо b. Если мы ищем коэффициент при
можно рассматривать как произведение 88 скобок; из каждой нужно выбрать в качестве множителя одно из слагаемых: либо а, либо b. Если мы ищем коэффициент при 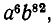 то нужно определить, каким числом способов можно выбрать из 88 букв а и b ровно шесть букв а. Но именно этот вопрос мы решали в примере 7 предыдущего параграфа, когда нужно было определить число различных аккордов из 6 нот.
то нужно определить, каким числом способов можно выбрать из 88 букв а и b ровно шесть букв а. Но именно этот вопрос мы решали в примере 7 предыдущего параграфа, когда нужно было определить число различных аккордов из 6 нот.
Благодаря замеченной общности задач мы могли бы воспользоваться уже готовым результатом; но мы повторим совсем коротко приведенные там рассуждения в новых терминах, относящихся уже к данной задаче.
Шесть букв а можно разместить на 88 возможных местах числом способов, равным произведению
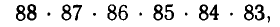
если выбрать эти буквы в определенном порядке. Поскольку порядок выбора букв нам безразличен, то каждая комбинация считается в этом произведении несколько раз: столько же, каким число способов можно переставлять между собой уже выбранные буквы на определенных шести местах.
Число возможных способов переставлять между собой шесть букв на шести местах, как мы уже видели, равно 6! Поэтому число различных способов выбрать шесть букв а из 88, а значит, и коэффициент при члене 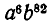 в разложении
в разложении 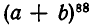 равно
равно
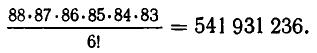
Легко догадаться, что коэффициент при 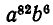 равен тому же числу. Соответствующее рассуждение уже приводилось в примере 4: способов выбрать по 82 буквы а из 88 равно столько же, сколько способов выбрать по 6, так как каждой группе по 6 букв соответствует определенная группа по 82 буквы, состоящая из оставшихся 82 мест. Но мы можем и не обращаться к этому рассуждению, рассматривая для члена
равен тому же числу. Соответствующее рассуждение уже приводилось в примере 4: способов выбрать по 82 буквы а из 88 равно столько же, сколько способов выбрать по 6, так как каждой группе по 6 букв соответствует определенная группа по 82 буквы, состоящая из оставшихся 82 мест. Но мы можем и не обращаться к этому рассуждению, рассматривая для члена 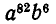 не выбор 82 букв а, а, наоборот, выбор шести букв b. Отсюда снова вытекает, что коэффициенты при
не выбор 82 букв а, а, наоборот, выбор шести букв b. Отсюда снова вытекает, что коэффициенты при 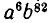 и а
и а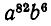 одинаковы.
одинаковы.
Определения и формулы
Примеров, рассмотренных в двух предыдущих параграфах, вполне достаточно, чтобы заметить некоторые общие закономерности и поставить общие задачи. Заметим прежде всего, что во всех рассмотренных примерах нам приходилось иметь дело с некоторыми конечными множествами и различными их под множествами.
Нас интересовало или число всех возможных подмножеств (пример 5 из § 2), или число подмножеств, обладающих определенным количеством элементов (примеры 4, 7 из § 1, примеры 1, 2, 3, 6 из § 2). В других случаях нужно было рассматривать упорядоченные подмножества, в которых элементы были расположены определенным образом (примеры 3, 6 из § 1, пример 4 из § 2). Здесь нам нужно было знать число различных упорядоченных подмножеств, считая различным образом упорядоченные подмножества различными. Наконец, встречалась и задача, в которой нужно было определить количество различных способов упорядочить данное конечное множество, то есть расположить его элементы в определенном порядке (пример 2, § 1). Все эти задачи можно теперь рассмотреть в общем виде.
Рассмотрим прежде всего точное определение упоминавшегося выше термина упорядоченное множество.
Конечное множество, состоящее из n элементов, называется упорядоченным, если его элементы каким-либо образом занумерованы, числами 1, 2, …, n.
«Номера», которые при этом приписываются элементам множества, позволяют мыслить элементы этого множества «расположенными» в каком-то «порядке»: первый элемент «предшествует» второму (а второй «следует» за первым), второй предшествует третьему и т. д.
Одно и то же конечное множество можно, разумеется, упорядочить разными способами. Например, множество учеников данного класса можно упорядочить по росту (опять-таки двумя противоположными способами), по весу, по возрасту, по алфавиту фамилий и т. д. и т. п.
Не следует, однако, думать, что каждый такой «порядок» связан непременно с каким-либо «естественным правилом» упорядочения. Скажем, множество шахматных фигур (каждого цвета по отдельности или все 32) можно, конечно, упорядочить слева направо в порядке их расстановки на доске или по силе (а фигуры одинаковой силы — слева направо или еще как угодно), но можно считать «упорядочением» и «беспорядочную» последовательность, в которой мы случайно поставили их на доску для данной партии. А можно было бы их просто расставить в ряд в произвольном «порядке». Аналогично множество учеников данного класса можно считать упорядоченным в соответствии с тем (в достаточной мере случайным!) порядком, в котором они сегодня пришли в школу.
Короче говоря, «нумерация», о которой говорится в определении упорядоченного множества, не предполагает, вообще говоря, никакого заранее известного «закона» — упорядочивая конечное множество, мы просто приписываем каким-либо образом номера его элементам. И если в приведенных примерах легко было все же указать некоторые «естественные» способы упорядочения, то для упорядочения, например, множества муравьев в муравейнике или рыб в озере трудно указать более «естественный» способ, чем переловить их всех по очереди и перенумеровать в порядке попадания их в банку или на удочку…
Таким образом, речь, как правило, идет лишь о теоретическом, мысленном упорядочении, которое для конечного множества всегда возможно.
В отличие от соглашений, принятых нами выше (Введение, п. 1 и п. 6) для множеств неупорядоченных, упорядоченные множества мы будем считать совпадающими (или равными) лишь тогда, когда они не только состоят из одних и тех же элементов, но и упорядочены (расположены, занумерованы и т. п.) одинаковым образом.
Говоря о различных упорядоченных множествах, состоящих из одних и тех же элементов, мы уже несколько раз называли их различными упорядочениями какого-либо множества. Этим термином нам будет удобно пользоваться и в дальнейшем.
Поскольку в этой главе нам придется иметь дело только с конечными множествами и их подмножествами, мы не будем много говорить о распространении понятия упорядоченности на общий случай бесконечных множеств, ограничившись определением и парой примеров.
Множество (безразлично — конечное или бесконечное) называется упорядоченным, если между его элементами установлено некоторое отношение, называемое отношением предшествования, обладающее следующими свойствами.
1) Для любых двух различных элементов а и b данного множества либо а предшествует b, либо b предшествует а.
2) Для любых элементов а, b и с данного множества из того, что а предшествует Ь, а Ь предшествует с, следует, что а предшествует с.
Примером упорядоченного множества может служить множество N натуральных чисел, «естественным» образом упорядоченное по величине: мы считаем, что n предшествует m , если n < m (можно, конечно, было бы выбрать и упорядочение, обратное «естественному», то есть считать, что n предшествует m , когда n > m ). Точно так же упорядочивается множество D всех действительных чисел. Множество K комплексных чисел, не обладающее никаким «естественным» порядком, можно, например, упорядочить, положив, что а+bi предшествует с+di, если а< с, а при а = с, если b < d. Все эти множества можно, разумеется, упорядочить и иными способами.
Введем теперь следующее
Определение:
Пусть дано конечное множество М, состоящее из m элементов. Размещением из m элементов по n элементов называют всякое упорядоченное подмножество множества М, состоящее из n элементов.
Из этого определения следует, что 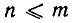 и что различные размещения отличаются друг от друга составом входящих в них элементов или порядком их расположения. Как видно из предыдущих параграфов, в комбинаторных задачах требуется знать число различных размещений из т элементов по n элементов. Это число принято обозначать символом
и что различные размещения отличаются друг от друга составом входящих в них элементов или порядком их расположения. Как видно из предыдущих параграфов, в комбинаторных задачах требуется знать число различных размещений из т элементов по n элементов. Это число принято обозначать символом 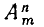 (А — первая буква французского слова аrrаngement, что означает размещение, приведение в порядок).
(А — первая буква французского слова аrrаngement, что означает размещение, приведение в порядок).
Теорема:
Число различных размещений из т элементов по n элементов равно произведению п последовательных натуральных чисел, начиная от m и до m — n + 1 включительно:

Доказательство:
Формула (1) была уже получена нами при разборе примера 4 в § 2. Здесь мы дадим вывод этой формулы, основанный на методе полной математической индукции. Индукцию будем вести по индексу n.
Пусть дано множество М, состоящее из т элементов. Очевидно, что число различных подмножеств этого множества, содержащих по одному элементу, равно числу m элементов М, то есть 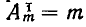 (подмножества из одного элемента автоматически упорядочены, так как содержат только первый элемент).
(подмножества из одного элемента автоматически упорядочены, так как содержат только первый элемент).
Далее, из каждого размещения по одному элементу можно получить различные размещения по два элемента, присоединяя к выбранному первому элементу второй. Так как для выбора второго элемента мы имеем уже m — 1 возможностей (один из элементов уже использован!), то
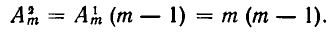
Предположим теперь, что для некоторого значения n — k справедлива формула
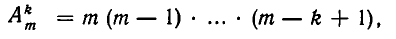
и докажем, что такая же формула имеет место и для n = k + 1. Пусть образованы все размещения из m элементов по k элементов. Размещения по k + 1 элементу могут быть получены присоединением к каждому из полученных еще одного элемента на (k + 1)-е место.
Из одного размещения по к элементов получится столько размещений по k + 1 элементу, сколько различных элементов можно присоединить, то есть m — k. Все получающиеся размещения будут различными, так как они отличаются последним элементом. Размещения по k + 1 элементу, получающиеся из различных размещений по k элементов, также не могут совпасть, поскольку их первые k элементов не совпадают. Остается добавить, что таким способом будут получены все размещения по k + 1 элементу. Отсюда следует, что число размещений по k + 1 элементу удовлетворяет равенству
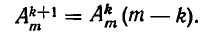
Воспользовавшись предположенной по индукции формулой для 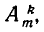 , найдем:
, найдем:
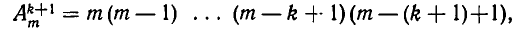
что и утверждалось. Справедливость этой формулы для n = 1 и n =2 была уже установлена выше; из принципа математической индукции следует, что формула (1) верна для всех 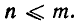
Определение:
Перестановками из n элементов называют различные упорядочения данного конечного множества, состоящего из n элементов.
Таким образом, различные перестановки отличаются друг от друга лишь порядком элементов. Число возможных различных перестановок из п элементов обозначается символом 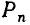 (от французского слова permutation— перестановка, перемещение).
(от французского слова permutation— перестановка, перемещение).
Теорема:
Число различных перестановок из n элементов равно произведению всех последовательных целых чисел, начиная от n и до 1 включительно:
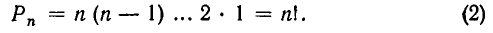
Доказательство этой теоремы окажется излишним, если мы заметим, что перестановки являются частным случаем размещений, а именно, при m = n. Значит, согласно формуле (1),
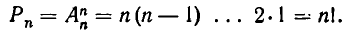
Впрочем, нетрудно доказать эту теорему и независимо от понятия размещения. Рассмотрим всевозможные перестановки из n элементов и подсчитаем, сколько из них начинаются одним и тем же определенным элементом. Если поставить выделенный элемент перед каждой из перестановок из остальных элементов, то мы получим все возможные перестановки, начинающиеся данным элементом. Следовательно, число всех перестановок из n элементов, начинающихся одним определенным элементом, равно 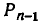 . Но тогда для числа всех возможных перестановок из n элементов находим:
. Но тогда для числа всех возможных перестановок из n элементов находим:

так как любой из п элементов может оказаться выделенным.
Формулу (3) можно использовать для доказательства нашей теоремы, пользуясь индукцией по числу элементов множества. Очевидно, что 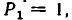 так как один элемент может находиться только на первом месте. Допустим, что формула (2) верна для множества, содержащего n — 1 элемент, то есть что
так как один элемент может находиться только на первом месте. Допустим, что формула (2) верна для множества, содержащего n — 1 элемент, то есть что
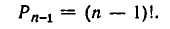
На основании формулы (3) найдем, что
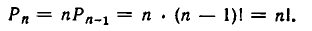
Таким образом, формула (2) верна для любого n.
Теорема:
Число различных размещений из m элементов по n элементов равно числу перестановок из m элементов, деленному на число перестановок из m — n элементов:

Доказательство:
Формулу (4) легко получить из формул (1) и (2). Действительно,
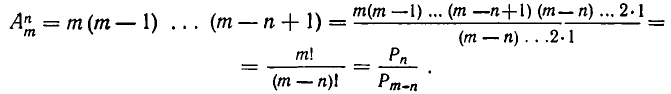
Это доказательство, несмотря на простоту и очевидность, часто вызывает чувство неудовлетворенности, так как сводится к формальным выкладкам и не показывает существа дела. Поэтому мы приведем еще одно доказательство, опирающееся только на определения размещений и перестановок.
Пусть дано некоторое множество из т элементов и все размещения его элементов по n. Из каждого такого размещения можно получить перестановку элементов множества, присоединив к нему в произвольном порядке остальные m — n элементов. В результате мы получим в с е перестановки из m элементов множества.
Следовательно, каждое размещение из m элементов по n элементов порождает столько перестановок по m элементов, сколькими различными способами к нему можно присоединить m — n оставшихся элементов. Так как это можно сделать 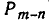 различными способами, то общее число перестановок из m элементов равно
различными способами, то общее число перестановок из m элементов равно
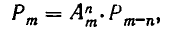
откуда и следует равенство (4).
Определение:
Пусть дано конечное множество M, состоящее из m элементов. Сочетанием из m элементов по n элементов называется любое подмножество УИ, содержащее п элементов.
Таким образом, сочетания являются неупорядоченным и подмножествами, и различные сочетания различаются между собой только составом элементов. Число всех возможных сочетаний из m элементов по n обозначают через 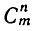 (от французского combinaison — сочетание, комбинация), а также через
(от французского combinaison — сочетание, комбинация), а также через 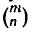 или С (m, n).
или С (m, n).
Теорема:
Число всех возможных сочетаний из m элементов по n элементов 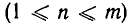 равно произведению n последовательных натуральных чисел от m до m — n + 1, деленному на произведение n последовательных натуральных чисел от n до 1:
равно произведению n последовательных натуральных чисел от m до m — n + 1, деленному на произведение n последовательных натуральных чисел от n до 1:
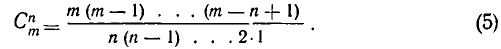
Доказательство этой теоремы сводится к доказательству следующего утверждения: число сочетаний из m элементов по n элементов равно числу размещений из m элементов по n элементов, деленному на число перестановок из n элементов. В самом деле, из этого утверждения, пользуясь формулами (1) и (2), легко получаем формулу (5).
Чтобы доказать теперь это утверждение, заметим, что каждое размещение из m элементов по n элементов может быть получено из такого же сочетания путем различных перестановок его элементов. Следовательно, каждое сочетание порождает столько размещений, сколько возможно различных перестановок его элементов. Отсюда следует, что 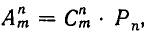 или
или

что и требовалось доказать.
Формулу (5) обычно приводят к более удобному для записи симметричному виду, умножая числитель и знаменатель на произведение всех натуральных чисел от m — n до 1 включительно. Тогда мы приходим к формуле:
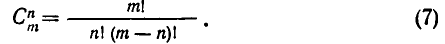
Формула (7) означает, что

Рекомендуем читателю самостоятельно разобраться в комбинаторном смысле этого равенства, доказавши его непосредственно, исходя лишь из определения перестановок и сочетаний.
Как было указано в формулировке теоремы 4, символ 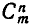 имеет смысл при
имеет смысл при 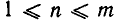 и означает количество подмножеств множества М , содержащих ровно по n элементов. Ясно, что
и означает количество подмножеств множества М , содержащих ровно по n элементов. Ясно, что 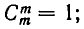 это следует и из формулы (5), но формулу (7) в этом случае приме нить нельзя, так как она будет содержать бессмысленный символ О!. Для общности принято полагать 0! = 1. В этом случае формула (7) дает для
это следует и из формулы (5), но формулу (7) в этом случае приме нить нельзя, так как она будет содержать бессмысленный символ О!. Для общности принято полагать 0! = 1. В этом случае формула (7) дает для 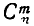 то же значение 1.
то же значение 1.
Удобно также ввести в рассмотрение символ 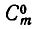 , что означает число пустых подмножеств множества М, то есть
, что означает число пустых подмножеств множества М, то есть 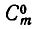 = 1. То же самое получится и из формулы (7), если воспользоваться принятым условием 0! = 1.
= 1. То же самое получится и из формулы (7), если воспользоваться принятым условием 0! = 1.
Принимаемое условие 0! = 1 имеет на самом деле более глубокий смысл, чем просто возможность вычислять 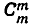 или
или 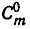 по формуле (7).
по формуле (7).
Более существенное основание для того, чтобы считать выражение 0! равным единице, состоит в следующем. Выражение n! можно рассматривать как функцию, определенную лишь для натурального аргумента 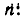
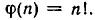 В своей области определения она удовлетворяет функциональному уравнению
В своей области определения она удовлетворяет функциональному уравнению 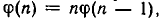 справедливость которого легко проверяется для всех натуральных
справедливость которого легко проверяется для всех натуральных 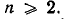 Действительно,
Действительно, 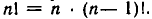 Если же в этом равенстве положить n = 1, то мы получим
Если же в этом равенстве положить n = 1, то мы получим 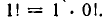
Однако все эти соображения являются не слишком убедительными, так как нельзя быть уверенным в том, что нам не встретится другая формула, в которой будет удобно полагать 0! равным какому-нибудь другому числу. Окончательное решение можно получить, идя вот каким путем. Естественно поставить вопрос: можно ли построить непрерывную функцию, определенную для всех значений х, и такую, которая для целых значений аргумента совпадает с 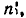 то есть доопределить функцию
то есть доопределить функцию 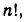 расширив ее область определения? Напомним, что в математическом анализе такое расширение производится, например, для показательной функции
расширив ее область определения? Напомним, что в математическом анализе такое расширение производится, например, для показательной функции 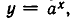 которая вначале была определена лишь для натурального показателя степени.
которая вначале была определена лишь для натурального показателя степени.
Поставленный вопрос был решен Эйлером и Гауссом. С помощью различных формул (Эйлер — через интеграл, а Гаусс — через бесконечное произведение) они определили функцию, обладающую нужным свойством, и доказали единственность такой функции при некоторых естественных предположениях. Эта функция называется гамма-функцией и обозначается Г(х). Она определена для всех х > 0 и удовлетворяет функциональному уравнению Г(х)= хГ(х — 1), а для натуральных n принимает значения Г(n) = (n — 1)!.
Обе формулы, определяющие функцию Г(х), имеют смысл при х=1 и определяют значение Г(1) = 1. Но в силу равенства Г(n) = (n — 1)! под выражением 0! следует понимать именно значение Г(1).
Все выведенные нами в настоящем параграфе формулы для числа размещений, перестановок и сочетаний фактически уже не однократно выводились нами ранее для различных частных конкретных случаев при рассмотрении примеров в § 1, 2. Рассмотрим еще некоторые свойства сочетаний, которые потребуются в дальнейшем.
Теорема:
Число сочетаний из т элементов по п элементов равно числу сочетаний из m элементов по m — n элементов:

Доказательство:
Формально равенство (9) легко получить из формулы для числа сочетаний, записанной в виде (7). Действительно,
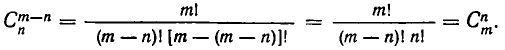
Комбинаторный смысл этого равенства также достаточно ясен. Каждому подмножеству из n элементов соответствует единственное определенное подмножество из m — n элементов—именно, тех, которые не вошли в первоначальное. Поэтому количество тех и других возможных подмножеств одинаково. При рассмотрении примеров (см. примеры 3 и 6 из § 2) мы фактически уже пользовались этим соображением.
Равенство (9) позволяет сокращать вычисления в тех случаях, когда n > m — n.
Теорема:
Число сочетаний из т элементов по п элементов равно сумме числа сочетаний из (m — 1) элементов по n элементов и по (n — 1) элементов:
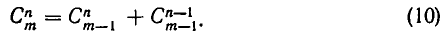
Доказательство, как и в предыдущем случае, проведем двумя различными способами. Прежде всего, пользуясь формулой (7) для числа сочетаний, находим:
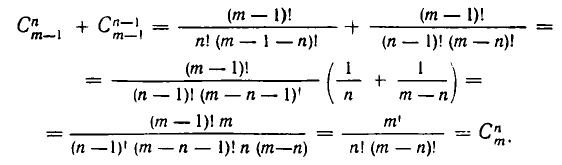
Второе доказательство состоит в следующем. Выделим некоторый фиксированный элемент а множества М и рассмотрим сочетания из m элементов по n элементов, содержащие или не содержащие этот элемент. Число сочетаний по n элементов, не содержащих элемента а, равно, очевидно, 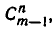 так как здесь рассматриваются подмножества по n элементов, образованные из элементов множества, содержащего m — 1 элемент (множество М без элемента а). Сочетания, содержащие а, можно получить так: образовать всевозможные сочетания по n — 1 элементу из того же множества М без элемента а и к каждому из них присоединить а. Отсюда ясно, что число таких сочетаний равно
так как здесь рассматриваются подмножества по n элементов, образованные из элементов множества, содержащего m — 1 элемент (множество М без элемента а). Сочетания, содержащие а, можно получить так: образовать всевозможные сочетания по n — 1 элементу из того же множества М без элемента а и к каждому из них присоединить а. Отсюда ясно, что число таких сочетаний равно 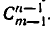 Так как каждое сочетание по n элементов либо содержит данный элемент а, либо не содержит его, то оно принадлежит либо одной, либо другой группе. Поэтому
Так как каждое сочетание по n элементов либо содержит данный элемент а, либо не содержит его, то оно принадлежит либо одной, либо другой группе. Поэтому
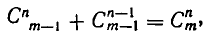
что и утверждалось
Размещения, перестановки и сочетания вместе часто называют одним словом — соединения.
Соединения с повторениями
Если рассмотреть теперь снова задачи, разобранные в §§ 1 и 2, то мы увидим, что решение почти всех из них не требует уже никаких рассуждений, а получается непосредственным применением нужной формулы из выведенных в предыдущем параграфе. Собственно говоря, все рассуждения, которые приводились при решении задач, были не чем иным, как именно выводом соответствующей формулы, но только для данного конкретного случая. Формулы § 3 потому и являются общими, что они применимы ко всем соединениям одного типа, и рассуждения, проведенные при выводе формул, освобождают нас от необходимости повторять их при решении каждой отдельной задачи.
Однако в числе приведенных там примеров есть и такие, которые не укладываются в уже рассмотренные схемы. К ним относятся, скажем, примеры 1 и 5 из § 1. Дело в том, что при определении различных видов соединений в предыдущем параграфе мы брали некоторое определенное множество, элементы которого существо вали «в единственном экземпляре» и в каждое данное соединение могли входить только один раз. Между тем в некоторых случаях элементы в соединении могут повторяться, как например ноты в музыкальной фразе в примере 5 из § 1. Для того чтобы охватить общей теорией и такие задачи, необходимо рассмотреть соединения с повторениями, которым и посвящен настоящий параграф.
Пусть имеется m непересекающихся множеств 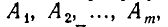 каждое из которых содержит не менее чем n элементов. Для простоты мы будем называть элементы множества
каждое из которых содержит не менее чем n элементов. Для простоты мы будем называть элементы множества 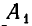 элементами 1-го сорта, элементы множества
элементами 1-го сорта, элементы множества 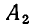 — элементами 2-го сорта, …, элементы множества
— элементами 2-го сорта, …, элементы множества 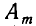 — элементами m-го сорта. Иначе говоря, мы рассматриваем разбиение (см. п. 7 Введения) некоторого множества
— элементами m-го сорта. Иначе говоря, мы рассматриваем разбиение (см. п. 7 Введения) некоторого множества 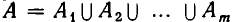 на непересекающиеся подмножества
на непересекающиеся подмножества 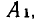
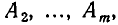 состоящие из элементов различных «сортов». Все элементы каждого подмножества, то есть элементы одного и того же сорта, будем считать одинаковыми, или совпадающими между собой.
состоящие из элементов различных «сортов». Все элементы каждого подмножества, то есть элементы одного и того же сорта, будем считать одинаковыми, или совпадающими между собой.
Слова «одинаковые» или «совпадающие» употребляются здесь в том смысле, в каком одинаковыми являются, например, 12 белых или 12 черных шашек. Именно в таком смысле понимается распространенное выражение «множество с повторяющимися элементами», хотя оно и не согласуется с описанным во Введении пониманием терминов «множество» и «элемент» (согласно которому множества, содержащие одни и те же элементы, считаются совпадающими).
Вообще, в таких случаях правильнее говорить о множестве различных вхождений «одинаковых» (точнее — одноименных) эле ментов. Так, слово «алгебра» состоит из ш е с т и букв, но содержит семь вхождений букв (буква «а» входит дважды, остальные — по одному разу). С совершенно аналогичной по существу ситуацией мы уже имели дело о гл. I, говоря о «кратных» корнях многочленов.
Из элементов множества A, то есть элементов, входящих в различные его подмножества 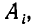 можно составлять различные упорядоченные множества, содержащие по n элементов в каждом. Такие упорядоченные множества принято называть размещениями с повторениями из элементов m сортов по n элементов, или, более коротко, просто размещениями с повторениями из m элементов по n.
можно составлять различные упорядоченные множества, содержащие по n элементов в каждом. Такие упорядоченные множества принято называть размещениями с повторениями из элементов m сортов по n элементов, или, более коротко, просто размещениями с повторениями из m элементов по n.
В первом из этих терминов (более точном, но менее употребительном из-за своей громоздкости) явным образом указывается, что имеется не т различных элементов, а m различных сортов элементов; число же элементов любого сорта в размещении может быть каким угодно.
Для наглядности будем представлять себе, что элементами рассматриваемых множеств являются буквы. Если, например, m=3, то это могут быть буквы а, b, с. Тогда возможны следующие размещения с повторениями этих трех элементов по n = 2:
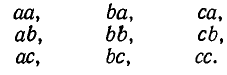
Размещения с повторениями можно рассматривать и в случае n > m, то есть неравенство 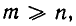 которое считалось необходимым в предыдущем параграфе, здесь необходимым уже не является. На пример, из m = 2 элемента а, b можно образовать размещения по n = 3 элемента. Они будут иметь вид:
которое считалось необходимым в предыдущем параграфе, здесь необходимым уже не является. На пример, из m = 2 элемента а, b можно образовать размещения по n = 3 элемента. Они будут иметь вид:
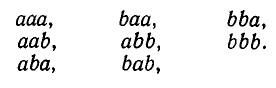
Число различных возможных размещений с повторениями из m элементов по n элементов будем обозначать 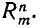
Теорема:
Число различных размещений с повторениями из m элементов по n элементов определяется по формуле:

Доказательство:
Прежде всего заметим, что размещения с повторениями по n элементов могут быть получены из размещений по (n — 1) элементу присоединением еще одного элемента. Так как к каждому размещению по (n — 1) элементу можно присоединить любой из имеющихся m элементов, то каждое размещение по (n — 1) элементу порождает т различных размещений по n элементов, то есть

Проведем теперь доказательство формулы (1) по индукции. Ясно, что при n = 1 число размещений равно m:
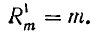
Допустим, что для некоторого числа n справедливо равенство
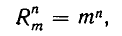
и найдем число размещений с повторениями из m элементов по n. Пользуясь формулой (2), получаем:
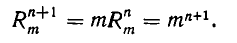
Таким образом, формула (1) справедлива для n — 1 и из ее справедливости для некоторого п следует и справедливость для n+1. Теорема доказана.
Для определения перестановки с повторениями рассмотрим множество, состоящее из п элементов, среди которых есть одинаковые. Как и раньше, мы можем представлять себе, что элементами этого множества являются буквы.
Определение:
Перестановкой с повторениями из n элементов называется любое упорядочение конечного множества, состоящего из n элементов, среди которых имеются совпадающие.
Пусть рассматриваемое множество состоит из  букв
букв  букв
букв  букв
букв 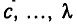 букв l. Подсчитаем число возможных перестановок с повторениями для такого множества.
букв l. Подсчитаем число возможных перестановок с повторениями для такого множества.
Занумеруем сначала все элементы а номерами 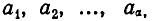 буквы b — номерами
буквы b — номерами  …, и т. д. и будем считать все эти элементы различными. Тогда мы имеем множество, состоящее из
…, и т. д. и будем считать все эти элементы различными. Тогда мы имеем множество, состоящее из
n различных элементов, и число перестановок этого множества, в силу теоремы 2 предыдущего параграфа, равно n!, причем
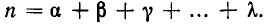
Теперь мы заметим, что элементы 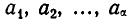 множества фактически не различаются между собой и поэтому среди всех n! перестановок имеются совпадающие, так что каждая перестановка с повторениями считается здесь несколько раз. Подсчитаем, сколько именно.
множества фактически не различаются между собой и поэтому среди всех n! перестановок имеются совпадающие, так что каждая перестановка с повторениями считается здесь несколько раз. Подсчитаем, сколько именно.
Ясно, что две перестановки, отличающиеся друг от друга лишь расположением элементов а, совпадают между собой. Таких перестановок существует столько, сколько возможно различных перестановок элементов 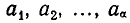 между собой, то есть
между собой, то есть 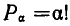 . Но то же самое относится и к элементу b: перестановки, отличающиеся лишь расположением элементов
. Но то же самое относится и к элементу b: перестановки, отличающиеся лишь расположением элементов 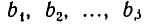 , совпадают между собой, и таких перестановок существует ровно
, совпадают между собой, и таких перестановок существует ровно 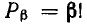 и т. д.
и т. д.
Следовательно, в числе n! перестановок всех элементов каждая считается 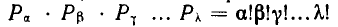 раз. Отсюда следует, что число различных перестановок с повторениями в нашем случае равно
раз. Отсюда следует, что число различных перестановок с повторениями в нашем случае равно
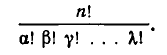
Обозначая число перестановок через 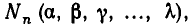 мы можем сформулировать полученный результат в виде следующей теоремы.
мы можем сформулировать полученный результат в виде следующей теоремы.
Теорема:
Число различных перестановок из п элементов, в ко торых элементы а, b, с, …, l повторяются соответственно 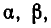
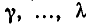 раз, выражается формулой
раз, выражается формулой
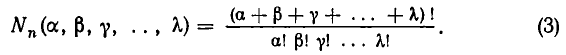
Определение:
Сочетанием с повторениями из m элементов по n элементов называется всякое множество, содержащее n элементов, каждый из которых является элементом одного из данных m сортов.
Как видно из этого определения, сочетания с повторениями являются неупорядоченными множествами, так что расположение эле ментов в них несущественно. Различные сочетания отличаются друг от друга входящими в них элементами, причем каждый элемент может входить в сочетание несколько раз.
Например, из трех элементов а, b, с можно образовать такие сочетания с повторениями по два элемента:
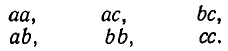
Из тех же трех элементов сочетания с повторениями по три эле мента будут следующими:
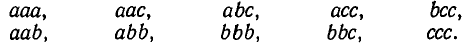
Ясно, что из элементов а, b, с можно составлять сочетания с повторениями и по четыре элемента и вообще по любому числу n элементов, так что для сочетаний с повторениями неравенство  не является необходимым, а можно рассматривать и случай m < n.
не является необходимым, а можно рассматривать и случай m < n.
Число различных возможных сочетаний с повторениями из m элементов по n элементов мы будем обозначать символом 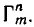 Для его нахождения можно воспользоваться следующей теоремой.
Для его нахождения можно воспользоваться следующей теоремой.
Теорема:
Число различных возможных сочетаний с повторения ми из т элементов по п элементов может быть найдено по формуле
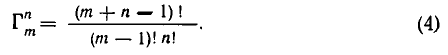
Доказательство:
Как уже говорилось выше, сочетания, в том числе с повторениями, являются неупорядоченными множествами. Поэтому всякое сочетание однозначно определяется тем, сколько элементов каждого сорта в него входит.
Например, если имеются элементы четырех сортов, то сочетание вполне определится, если сказать, что оно содержит два эле мента первого сорта, четыре элемента второго, ни одного элемента третьего и один элемент четвертого сорта. Это есть одно из возможных сочетаний с повторениями из четырех элементов по семи. Такое сочетание можно условно записать комбинацией четырех чисел (2, 4, 0, 1), показывающей, сколько элементов каждого сорта берется.
Другие сочетания определятся, например, комбинациями (3, 0, 0, 4) или (1, 1,2, 3). Первая из них определяет сочетание, состоящее из трех элементов первого сорта и четырех элементов четвертого. Элементы второго и третьего сорта в это сочетание не входят. Вторая комбинация определяет сочетание, содержащее один элемент первого сорта, один — второго, два — третьего и три элемента четвертого сорта. Заметим еще, что, пока мы рассматриваем сочетания из четырех элементов по семи, условная запись представляет комбинацию всегда четырех чисел — по одному числу на каждый имеющийся сорт элементов, и сумма этих чисел всегда равна семи, то есть общему числу элементов, входящих в сочетание.
В общем случае, если мы захотим условной комбинацией чисел изобразить некоторое сочетание с повторением из m элементов по n элементов, то придется написать уже m целых неотрицательных чисел, снова по одному числу на каждый имеющийся сорт элементов, обозначив их, скажем, 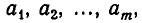 причем сумма этих чисел должна равняться числу элементов в сочетании, то есть n:
причем сумма этих чисел должна равняться числу элементов в сочетании, то есть n:

Такую комбинацию мы будем записывать в виде 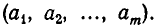
Комбинацию 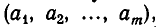 , определяющую сочетание, можно записать, пользуясь только цифрами 1 и 0. Сделаем это следующим образом. Вместо числа а 4, означающего количество элементов первого сорта в сочетании, напишем такое же число единиц. Затем таким же способом запишем число элементов второго сорта, а между этими двумя группами единиц поставим нуль для их разделения. Так же будем поступать и дальше. Комбинация (1, 1, 2, 3) изобразится тогда как (1010110111), а комбинация (2, 1, 2, 2) — как (1101011011). Запись (1011011101) соответствует комбинации (1, 2, 3, 1).
, определяющую сочетание, можно записать, пользуясь только цифрами 1 и 0. Сделаем это следующим образом. Вместо числа а 4, означающего количество элементов первого сорта в сочетании, напишем такое же число единиц. Затем таким же способом запишем число элементов второго сорта, а между этими двумя группами единиц поставим нуль для их разделения. Так же будем поступать и дальше. Комбинация (1, 1, 2, 3) изобразится тогда как (1010110111), а комбинация (2, 1, 2, 2) — как (1101011011). Запись (1011011101) соответствует комбинации (1, 2, 3, 1).
Если какое-либо из чисел 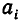 равно нулю, то есть элементы данного сорта в сочетание не входят, то единиц на этом месте писать не будем, и два или несколько нулей могут тогда оказаться рядом. Например, комбинация (2, 4, 0, 1) запишется в виде (1101111001). Запись (1111000111) соответствует комбинации (4, 0, 0, 3).
равно нулю, то есть элементы данного сорта в сочетание не входят, то единиц на этом месте писать не будем, и два или несколько нулей могут тогда оказаться рядом. Например, комбинация (2, 4, 0, 1) запишется в виде (1101111001). Запись (1111000111) соответствует комбинации (4, 0, 0, 3).
Запись из нулей и единиц, соответствующая сочетанию из m элементов по n элементов, будет содержать ровно n единиц и m — 1 нулей. Действительно, количество единиц равно числу элементов в сочетании, а количество нулей на единицу меньше числа сортов элементов, поскольку нуль употребляется лишь для их разделения. Поэтому число сочетаний с повторениями из m элементов по n элементов равно числу перестановок из n единиц и m — 1 нулей. Как уже известно из теоремы 2, это число равно
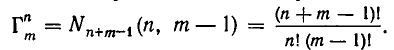
Теорема доказана.
Если сравнить полученное выражение с формулой (7) для числа сочетаний без повторений, выведенной в предыдущем параграфе, то мы заметим, что
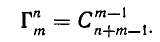
Таким образом, число сочетаний с повторениями из m элементов по n элементов равно числу сочетаний без повторений из n + m — 1 элементов по m — 1 элементов.
В этом параграфе мы рассмотрим еще несколько комбинаторных задач, при решении которых будем пользоваться установленными выше формулами и правилами.
Пример:
В некотором государстве каждые два человека отличаются набором зубов. Каково максимально возможное число жителей этого государства, если наибольшее число зубов у человека равно 32?
Решение:
Эту задачу можно решить двумя способами. Первый способ заключается в том, что мы сначала ищем, сколько людей может иметь k зубов, а потом просуммируем полученные результаты от k= 0 до k=32. Ясно, что k мест из 32 можно выбрать 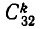 способами. Поэтому ровно кkзубов имеют не более чем
способами. Поэтому ровно кkзубов имеют не более чем 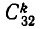 жителей. А тогда общее число жителей не превосходит
жителей. А тогда общее число жителей не превосходит
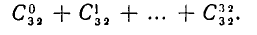
Полученный этим способом ответ оказался очень громоздким. Выгоднее избрать другой путь, которым мы уже пользовались при решении примера 5 в § 2, — применить метод индукции.
Если речь идет об одном зубе, то возможны только два человека—один с зубом и второй без него. При двух зубах число возможных наборов зубов становится равным четырем: нет ни одного зуба, есть первый, есть второй и есть оба.
Увеличив число зубов до трех, мы удвоим число возможностей и получим восемь различных наборов. Действительно, каждый из рассмотренных наборов двух зубов может встретиться дважды — когда нет третьего зуба и когда он есть.
Обозначим число возможных наборов k зубов через 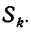 Предыдущими рассуждениями мы доказали, что
Предыдущими рассуждениями мы доказали, что 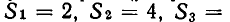
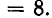 Допустим, что для некоторого k справедливо равенство
Допустим, что для некоторого k справедливо равенство 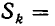
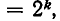 и докажем, что аналогичное равенство справедливо и для случая k + 1 зубов. Среди всех различных наборов, входящих в
и докажем, что аналогичное равенство справедливо и для случая k + 1 зубов. Среди всех различных наборов, входящих в 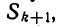 имеется ровно
имеется ровно 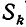 наборов, в которых отсутствует (k+1)-й зуб, и столько же наборов, в которых (k+1)-й зуб имеется. Поэтому
наборов, в которых отсутствует (k+1)-й зуб, и столько же наборов, в которых (k+1)-й зуб имеется. Поэтому
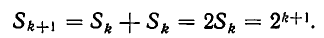
Таким образом, при возможных n зубах число всех людей, отличающихся набором зубов, равно 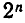 . В нашем случае n = 32, поэтому мы получаем
. В нашем случае n = 32, поэтому мы получаем 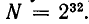 Как известно,
Как известно, 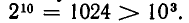 Поэтому
Поэтому 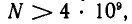 так что возможное население этого государства больше нынешнего населения всего земного шара.
так что возможное население этого государства больше нынешнего населения всего земного шара.
Заметим, что полученный нами результат на самом деле дает больше, чем только оценку возможного населения забавного государства. Сравнивая полученное значение N с написанным выше выражением N как суммы сочетаний, мы приходим к формуле:
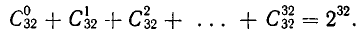
Более того, из приведенного выше доказательства по индукции вытекает, что аналогичное равенство справедливо при любом n, то есть что имеет место формула
Пример:
Дана прямоугольная сетка квадратов размером m х n. Каково число различных дорог на этой сетке, ведущих из левого верхнего угла в правый нижний (рис. 46)? (Все звенья дороги предполагаются идущими или вправо, или вниз — без возвращений; сходная ситуация возникает, скажем, при выборе одного из кратчайших маршрутов между двумя городскими перекрестками.)
Решение:
Всякая дорога представляет собой ломаную, содержащую m горизонтальных и n вертикальных звеньев, то есть состоящую из m + n звеньев. Различные дороги отличаются одна от другой лишь порядком чередования горизонтальных и вертикальных звеньев. Поэтому число возможных дорог равно числу способов, которыми можно выбрать n вертикальных отрезкoв из общего числа m + n отрезков, а следовательно, есть 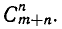
Можно было бы рассматривать число способов выбора не n вертикальных, а m горизонтальных отрезков и тогда мы получили бы ответ 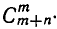 Но формула (9) из § 3 показывает, что
Но формула (9) из § 3 показывает, что 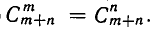
Полученный результат можно использовать для вывода еще одной интересной формулы. Пусть наша сетка является квадрат ной, то есть имеет размеры n х n. Тогда из приведенного выше решения следует, что число различных дорог, соединяющих левый верхний угол с правым нижним, равно 
Вместе с тем число этих дорог можно подсчитать иначе. Рассмотрим диагональ, идущую из нижнего левого угла в верхний правый, и обозначим вершины, лежащие на этой диагонали, через 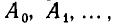
 Так как каждая дорога обязательно проходит через одну — и притом единственную—точку этой диагонали, то общее число дорог есть сумма числа дорог, идущих через точку
Так как каждая дорога обязательно проходит через одну — и притом единственную—точку этой диагонали, то общее число дорог есть сумма числа дорог, идущих через точку  через точку
через точку 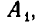 через точку
через точку 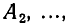 через точку
через точку 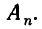
Найдем число возможных дорог, идущих через точку 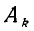
 Если нумерация точек произведена снизу вверх, ка это показано на рис. 47, то точка
Если нумерация точек произведена снизу вверх, ка это показано на рис. 47, то точка  отстоит от нижней горизонтали на расстоянии k, считая за единицу измерения длину стороны квадрата сетки. От правой вертикали ее отделяют тогда n— k горизонтальных отрезка.
отстоит от нижней горизонтали на расстоянии k, считая за единицу измерения длину стороны квадрата сетки. От правой вертикали ее отделяют тогда n— k горизонтальных отрезка.
Дорог, соединяющих верхний левый угол с точкой  , будет тогда
, будет тогда 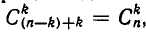 , а дорог, соединяющих точку
, а дорог, соединяющих точку 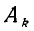 с нижним правым углом, будет
с нижним правым углом, будет 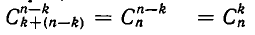 (это видно из рассмотрения равных прямоугольников, противоположными вершинами которых служат верхний левый угол исходного квадрата и точка
(это видно из рассмотрения равных прямоугольников, противоположными вершинами которых служат верхний левый угол исходного квадрата и точка 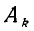 и соответственно точка
и соответственно точка 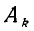 и нижний правый угол квадрата). Поэтому общее число дорог, соединяющих верхний левый угол с нижним правым и проходящих через
и нижний правый угол квадрата). Поэтому общее число дорог, соединяющих верхний левый угол с нижним правым и проходящих через 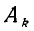 , равно
, равно 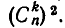 Но тогда общее число всех дорог равно сумме
Но тогда общее число всех дорог равно сумме
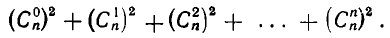
Сравнивая полученную сумму с найденным выше выражением для числа дорог, мы придем к формуле:
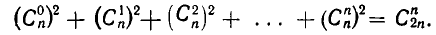
Пример:
Шесть пассажиров садятся на остановке в трамвайный поезд, состоящий из трех трамвайных вагонов. Каким числом различных способов могут они распределиться в вагонах?
Решение:
Прежде всего необходимо указать, что задача сформулирована недостаточно точно и допускает два различных толкования. Нас может интересовать или только число пассажиров в каждом вагоне или же кто именно в каком вагоне находится. Рассмотрим обе возможные формулировки.
Сначала рассмотрим случай, когда учитывается, кто в каком вагоне находится, то есть когда случаи «пассажир А в первом вагоне, а пассажир В — во втором» и «пассажир В в первом вагоне, а пассажир А — во втором» считаются различными.
Здесь мы имеем размещения с повторениями из трех элементов по шесть элементов: для каждого из шести пассажиров имеются три возможности. Пользуясь формулой (1) из § 4, получаем, что число различных способов, которыми шесть пассажиров могут распределиться в трех вагонах, равно:
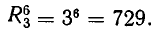
Иной результат получится в том случае, если нас интересует лишь число пассажиров в каждом вагоне, так что случай «один пассажир в первом вагоне и один во втором» является единственным, независимо от того, кто из пассажиров где находится. Здесь нужно подсчитывать уже не размещения, а Сочетания с повторениями. По формуле (4) из §4 находим, что число различных способов распределения пассажиров в этом случае равно
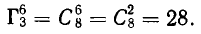
Пример:
Сколькими способами можно распределить 28 костей домино между 4 игроками так, чтобы каждый получил 7 костей?
Решение:
Первый игрок может выбрать 7 костей 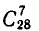 способами. После этого второй игрок должен выбрать 7 костей из оставшихся 21 кости. Это можно сделать
способами. После этого второй игрок должен выбрать 7 костей из оставшихся 21 кости. Это можно сделать 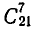 способами. Третий игрок может выбрать кости
способами. Третий игрок может выбрать кости 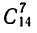 способами, а четвертый —
способами, а четвертый — 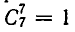 способом. Всего получаем
способом. Всего получаем
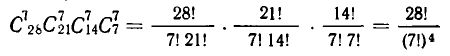
способов раздела костей.
Эту задачу можно решить иначе. Упорядочим все кости и отдадим первые 7 костей первому игроку, вторые 7 костей — второму игроку и т. д. Так как 28 костей можно упорядочить 28! способами, то получаем 28! способов раздела. Но некоторые из этих способов приводят к одинаковым результатам — игрокам неважно, в каком порядке приходят к ним кости, а важно лишь, какие именно кости они получат. Поэтому результат не изменится, если мы как угодно переставим друг с другом первые 7 костей, потом вторые 7 костей и т. д. Первые 7 костей можно переставить 7! способами, вторые 7 костей — тоже 7! способами и т. д. Всего получим 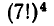 перестановок, дающих то же распределение костей, что и данная. Поэтому число способов раздела костей равно
перестановок, дающих то же распределение костей, что и данная. Поэтому число способов раздела костей равно
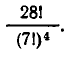
Пример:
Сколькими способами можно разделить 40 яблок между 4 мальчиками (все яблоки считаются одинаковыми)?
Решение:
Возьмем три одинаковые перегородки и рассмотрим всевозможные перестановки 43 предметов: 40 яблок и 3 пере городок. Каждой такой перестановке соответствует свой способ раздела: первый мальчик получает все яблоки от начала до первой перегородки, второй — все яблоки между первой и второй перегородками, третий — все яблоки между второй и третьей перегородками, а четвертый — все остальные яблоки. (Если, например, первая и вторая перегородки оказались рядом, то второй мальчик ничего не получает.) Значит, число способов раздела равно числу перестановок 40 яблок и 3 перегородок. По формуле числа перестановок с повторениями получаем, что это число равно
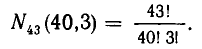
Пример:
Сколькими способами можно разделить 40 яблок между 4 мальчиками так, чтобы каждый получил по крайней мере 3 яблока (все яблоки по-прежнему считаются одинаковыми)?
Решение:
Сначала дадим каждому мальчику по 3 яблока. А потом разделим оставшиеся 28 яблок так, как было сделано в предыдущей задаче. Всего получаем
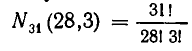
способов раздела.
Пример:
Имеется m различных сигнальных флагов и k мачт, на которых их вывешивают. Значение сигнала зависит от того, в каком порядке развешаны флаги. Сколько сигналов можно передать этими флагами, если все флаги должны быть использованы, но некоторые из мачт могут оказаться пустыми?
Решение:
Добавим к m флагам k — 1 перегородку и рассмотрим всевозможные перестановки из m различных флагов и k одинаковых перегородок. Как ив примере 5, каждой перестановке соответствует свой сигнал (на первую мачту вывешиваются по порядку все флаги от начала до первой перегородки и т. д.). Поэтому число сигналов равно числу таких перестановок, то есть равно
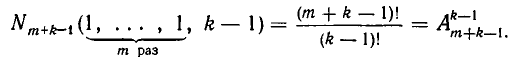
Если бы мы не потребовали, чтобы все флаги были использованы, то число сигналов оказалось бы больше. В этом случае задача решалась бы в два этапа. Сначала выберем, какие флаги будут участвовать в сигнале. Если число выбираемых флагов равно s, то выбор можно сделать 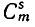 способами. Как мы уже знаем, с помощью данных s флагов можно передать
способами. Как мы уже знаем, с помощью данных s флагов можно передать 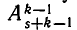 сигналов. По этому всего имеем
сигналов. По этому всего имеем 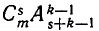 сигналов, передаваемых s флагами. А общее число сигналов равно
сигналов, передаваемых s флагами. А общее число сигналов равно
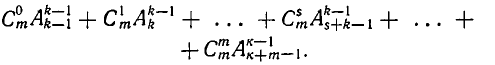
Бином Ньютона и его обобщения
В главе I (§ 1, п. 8) была выведена формула бинома Ньютона:
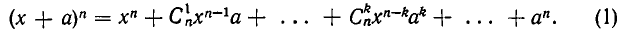
Через 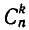 мы обозначили коэффициент при
мы обозначили коэффициент при 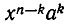 в разложении
в разложении 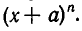 Для
Для 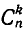 было получено соотношение
было получено соотношение 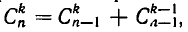 которое позволяет вычислять эти коэффициенты один за другим. Сейчас мы получим явную формулу для
которое позволяет вычислять эти коэффициенты один за другим. Сейчас мы получим явную формулу для 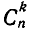 — для этого мы покажем, что коэффициенты
— для этого мы покажем, что коэффициенты 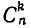 — не что иное, как число сочетаний из n элементов по k (именно поэтому в гл. I и было выбрано обозначение
— не что иное, как число сочетаний из n элементов по k (именно поэтому в гл. I и было выбрано обозначение 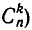
В самом деле, запишем 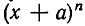 в виде произведения n сомножителей:
в виде произведения n сомножителей:
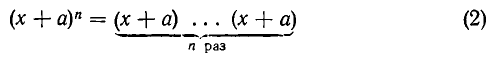
— и раскроем скобки в этом произведении, причем будем записывать все множители в том порядке, в котором они нам встретятся. Например, запишем
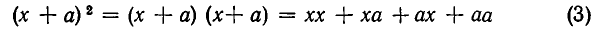
или
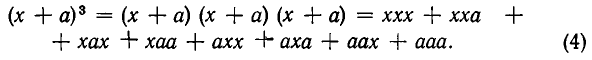
Видно, что в формулу (3) входят все размещения с повторениями из букв х и а, по две буквы в каждом размещении , а в формулу (4) — размещения с повторениями из тех же букв, содержащие по три буквы. То же самое будет в общем случае — после раскрытия скобок в формуле (2) получаются все размещения с повторениями из букв х и а, по n букв в каждом размещении.
Приведем подобные члены. Подобными будут члены, содержащие одинаковое количество букв а (тогда и букв х в них будет поровну). Найдем число членов, содержащих k букв а (и, следовательно, n — k букв х). Эти члены являются всевозможными перестановками с повторениями, составленными из k букв а и n — k букв Их число равно
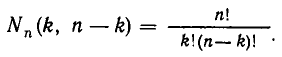
Отсюда вытекает, что после приведения подобных членов коэффициент при 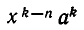 окажется равным
окажется равным 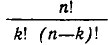 , то есть числу сочетаний из n элементов по k. Тем самым доказано, что числа
, то есть числу сочетаний из n элементов по k. Тем самым доказано, что числа 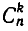 в формуле (1) действительно являются числами сочетаний из n элементов по k .
в формуле (1) действительно являются числами сочетаний из n элементов по k .
Рассмотрим несколько задач, связанных с формулой бинома Ньютона.
Пример:
Определить коэффициент при 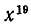 в разложении
в разложении 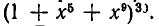
Решение:
Запишем данное нам выражение в виде:
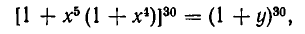
где 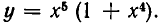 Отсюда видно, что
Отсюда видно, что 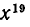 может получиться только из члена, содержащего
может получиться только из члена, содержащего 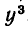 . В соответствии с формулой (1) этот член имеет вид:
. В соответствии с формулой (1) этот член имеет вид:
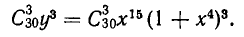
Для получения 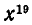 нужно при раскрытии скобок взять член, содержащий
нужно при раскрытии скобок взять член, содержащий 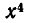 в первой степени. Этот член имеет вид
в первой степени. Этот член имеет вид 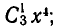 поэтому искомый коэффициент при
поэтому искомый коэффициент при 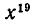 равен произведению
равен произведению
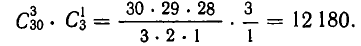
Пример:
С каким коэффициентом входит 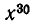 в разложение
в разложение 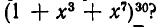
Решение:
Выясним сначала, каким числом способов можно представить 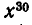 в виде произведений
в виде произведений 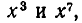 для чего надо знать, какими способами можно представить число 30 в виде суммы слагаемых 3 и 7. Очевидно, что 30 можно представить в виде суммы десяти троек, и без участия слагаемого 7 других представлений нет. С участием 7 возможно только одно представление 30 = 7+7+7+3+3+3, так как число семерок, входящих в сумму, должно быть кратно трем, иначе сумма не будет делиться на 3.
для чего надо знать, какими способами можно представить число 30 в виде суммы слагаемых 3 и 7. Очевидно, что 30 можно представить в виде суммы десяти троек, и без участия слагаемого 7 других представлений нет. С участием 7 возможно только одно представление 30 = 7+7+7+3+3+3, так как число семерок, входящих в сумму, должно быть кратно трем, иначе сумма не будет делиться на 3.
Итак, для нахождения коэффициента при 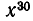 в
в 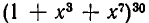 нам нужно определить коэффициенты при членах
нам нужно определить коэффициенты при членах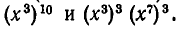
Как и в предыдущем примере, перепишем наше выражение в виде 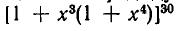 и воспользуемся формулой (1):
и воспользуемся формулой (1):
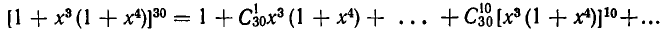
Слагаемое 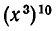 есть только в последнем из выписанных нами членов, и коэффициент при нем равен
есть только в последнем из выписанных нами членов, и коэффициент при нем равен 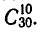 Еще одно слагаемое вида
Еще одно слагаемое вида 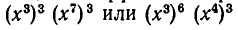 входит в слагаемое
входит в слагаемое
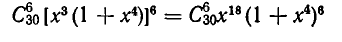
при раскрытии произведения 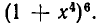
Так как в этой последней скобке коэффициент при 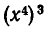 равен
равен 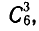 то коэффициент при члене
то коэффициент при члене 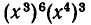 равен произведению
равен произведению 
Окончательно, искомый коэффициент при 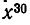 есть сумма
есть сумма
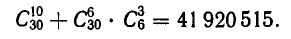
Подставляя в (1) х=1, получим другой вывод формулы (1) из § 5. Аналогично, приняв в (1) х = — 1, получим еще одну любопытную формулу:
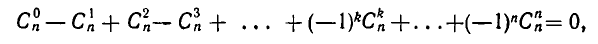
или, иначе,
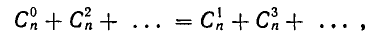
то есть для любого n сумма сочетаний из n элементов по четному числу элементов равна сумме сочетаний из п элементов по нечетному числу элементов.
Формулу, аналогичную формуле бинома Ньютона, можно получить и для возведения в степень суммы нескольких слагаемых. Если число слагаемых невелико, то ее легко получить, применяя несколько раз формулу бинома Ньютона. Например, для трех слагаемых можно написать:
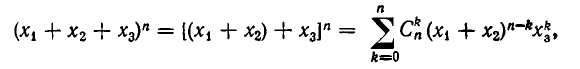
раскрывая, в свою очередь, каждое слагаемое справа по формуле (2). При небольших n это нетрудно сделать.
Пусть, например, n = 2. Тогда получаем:
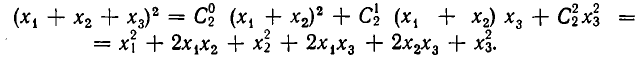
При n = 3 находим:
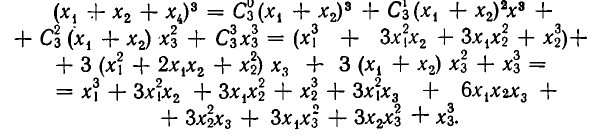
Таким образом, мы получили формулы для квадрата и куба суммы трех слагаемых, которые имеют вид:
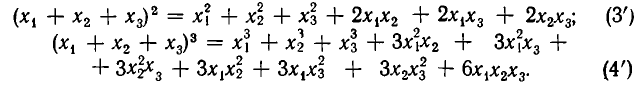
Однако для больших n, не говоря уже о большом числе слагаемых , такой способ вывода формулы потребует уже чересчур сложных и громоздких вычислений.
Формулу для возведения в степень суммы нескольких слагаемых можно получить и непосредственно, подобно тому как мы это делали для формулы бинома Ньютона.
Действительно, n-я степень суммы 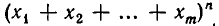 есть произведение n одинаковых слагаемых вида
есть произведение n одинаковых слагаемых вида 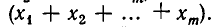 Перемножив все скобки, мы получим сумму произведений, причем в каждом слагаемом будет n сомножителей. Общее число слагаемых равно числу размещений с повторениями из m элементов по n элементов, то есть
Перемножив все скобки, мы получим сумму произведений, причем в каждом слагаемом будет n сомножителей. Общее число слагаемых равно числу размещений с повторениями из m элементов по n элементов, то есть 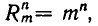 так как множители, взятые из различных скобок, могут совпадать. Вследствие этого каждое отдельное слагаемое будет иметь вид
так как множители, взятые из различных скобок, могут совпадать. Вследствие этого каждое отдельное слагаемое будет иметь вид
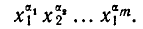
Показатели степени 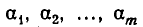 а удовлетворяют, очевидно, условиям
а удовлетворяют, очевидно, условиям 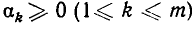 и
и

то есть все они суть целые неотрицательные числа и их сумма равна n.
Чтобы определить коэффициент, который будет стоять у произведения 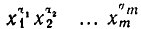 после приведения подобных членов, нужно подсчитать, сколько раз такое произведение может встретиться. Это можно сделать следующим образом.
после приведения подобных членов, нужно подсчитать, сколько раз такое произведение может встретиться. Это можно сделать следующим образом.
Каждому произведению (до приведения подобных членов) поставим в соответствие перестановку из элементов 1, 2, …, m . При этом если из первой скобки берется, например, множитель  из второй —
из второй —  из третьей —
из третьей — 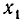 и т. д., то перестановка имеет вид 2, 3, 1 … . Иначе говоря, в перестановке на первом месте ставится номер элемента, взятого из первой скобки, на втором — номер элемента из второй скобки и т.д. Например, произведению
и т. д., то перестановка имеет вид 2, 3, 1 … . Иначе говоря, в перестановке на первом месте ставится номер элемента, взятого из первой скобки, на втором — номер элемента из второй скобки и т.д. Например, произведению 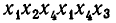 соответствует перестановка 1, 2, 4, 1, 4, 3.
соответствует перестановка 1, 2, 4, 1, 4, 3.
Ясно, что произведению 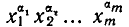 ставится в соответствие такая перестановка, в которой элемент 1 повторяется на различных местах ровно
ставится в соответствие такая перестановка, в которой элемент 1 повторяется на различных местах ровно 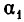 раз, элемент 2— ровно
раз, элемент 2— ровно 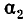 раз и т. д. В том случае, когда
раз и т. д. В том случае, когда 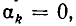 что возможно, соответствующий элемент к не входит в рассматриваемую перестановку вовсе.
что возможно, соответствующий элемент к не входит в рассматриваемую перестановку вовсе.
Из сказанного вытекает, что произведение 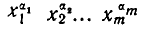 встречается среди слагаемых столько раз, сколько существует различных перестановок с повторениями из п элементов, в которых элемент 1 повторяется
встречается среди слагаемых столько раз, сколько существует различных перестановок с повторениями из п элементов, в которых элемент 1 повторяется 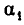 раз, элемент 2 повторяется
раз, элемент 2 повторяется 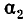 раз,…, элемент m повторяется
раз,…, элемент m повторяется 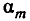 раз, то есть
раз, то есть
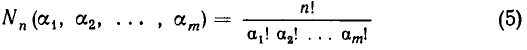
(см. формулу (3) из § 4). Это же число служит коэффициентом при произведении 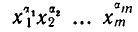 в разложении n-й степени суммы m слагаемых.
в разложении n-й степени суммы m слагаемых.
Полученное можно выразить в виде следующей теоремы.
Теорема:
Результат возведения суммы m слагаемых в n-ю степень имеет вид:
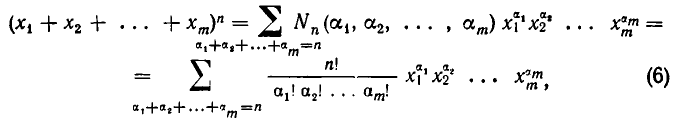
где суммирование распространяется на все возможные системы  целых неотрицательных чисел, удовлетворяющие условию
целых неотрицательных чисел, удовлетворяющие условию 
Эту теорему называют полиномиальной, а коэффициенты (5) — полиномиальными коэффициентами.
Легко убедиться в том, что формула бинома Ньютона является частным случаем полиномиальной формулы (6).
Решение заданий и задач по предметам:
Дополнительные лекции по высшей математике:
- Тождественные преобразования алгебраических выражений
- Функции и графики
- Преобразования графиков функций
- Квадратная функция и её графики
- Алгебраические неравенства
- Неравенства
- Неравенства с переменными
- Прогрессии в математике
- Арифметическая прогрессия
- Геометрическая прогрессия
- Показатели в математике
- Логарифмы в математике
- Исследование уравнений
- Уравнения высших степеней
- Уравнения высших степеней с одним неизвестным
- Комплексные числа
- Непрерывная дробь (цепная дробь)
- Алгебраические уравнения
- Неопределенные уравнения
- Соединения
- Бином Ньютона
- Число е
- Непрерывные дроби
- Функция
- Исследование функций
- Предел
- Интеграл
- Двойной интеграл
- Тройной интеграл
- Интегрирование
- Неопределённый интеграл
- Определенный интеграл
- Криволинейные интегралы
- Поверхностные интегралы
- Несобственные интегралы
- Кратные интегралы
- Интегралы, зависящие от параметра
- Квадратный трехчлен
- Производная
- Применение производной к исследованию функций
- Приложения производной
- Дифференциал функции
- Дифференцирование в математике
- Формулы и правила дифференцирования
- Дифференциальное исчисление
- Дифференциальные уравнения
- Дифференциальные уравнения первого порядка
- Дифференциальные уравнения высших порядков
- Дифференциальные уравнения в частных производных
- Тригонометрические функции
- Тригонометрические уравнения и неравенства
- Показательная функция
- Показательные уравнения
- Обобщенная степень
- Взаимно обратные функции
- Логарифмическая функция
- Уравнения и неравенства
- Положительные и отрицательные числа
- Алгебраические выражения
- Иррациональные алгебраические выражения
- Преобразование алгебраических выражений
- Преобразование дробных алгебраических выражений
- Разложение многочленов на множители
- Многочлены от одного переменного
- Алгебраические дроби
- Пропорции
- Уравнения
- Системы уравнений
- Системы уравнений высших степеней
- Системы алгебраических уравнений
- Системы линейных уравнений
- Системы дифференциальных уравнений
- Арифметический квадратный корень
- Квадратные и кубические корни
- Извлечение квадратного корня
- Рациональные числа
- Иррациональные числа
- Арифметический корень
- Квадратные уравнения
- Иррациональные уравнения
- Последовательность
- Ряды сходящиеся и расходящиеся
- Тригонометрические функции произвольного угла
- Тригонометрические формулы
- Обратные тригонометрические функции
- Теорема Безу
- Математическая индукция
- Показатель степени
- Показательные функции и логарифмы
- Множество
- Множество действительных чисел
- Числовые множества
- Преобразование рациональных выражений
- Преобразование иррациональных выражений
- Геометрия
- Действительные числа
- Степени и корни
- Степень с рациональным показателем
- Тригонометрические функции угла
- Тригонометрические функции числового аргумента
- Тригонометрические выражения и их преобразования
- Преобразование тригонометрических выражений
- Вычислительная математика
- Прямая линия на плоскости и ее уравнения
- Прямая и плоскость
- Линии и уравнения
- Прямая линия
- Уравнения прямой и плоскости в пространстве
- Кривые второго порядка
- Кривые и поверхности второго порядка
- Числовые ряды
- Степенные ряды
- Ряды Фурье
- Преобразование Фурье
- Функциональные ряды
- Функции многих переменных
- Метод координат
- Гармонический анализ
- Вещественные числа
- Предел последовательности
- Аналитическая геометрия
- Аналитическая геометрия на плоскости
- Аналитическая геометрия в пространстве
- Функции одной переменной
- Высшая алгебра
- Векторная алгебра
- Векторный анализ
- Векторы
- Скалярное произведение векторов
- Векторное произведение векторов
- Смешанное произведение векторов
- Операции над векторами
- Непрерывность функций
- Предел и непрерывность функций нескольких переменных
- Предел и непрерывность функции одной переменной
- Производные и дифференциалы функции одной переменной
- Частные производные и дифференцируемость функций нескольких переменных
- Дифференциальное исчисление функции одной переменной
- Матрицы
- Линейные и евклидовы пространства
- Линейные отображения
- Дифференциальные теоремы о среднем
- Теория устойчивости дифференциальных уравнений
- Функции комплексного переменного
- Преобразование Лапласа
- Теории поля
- Операционное исчисление
- Системы координат
- Рациональная функция
- Интегральное исчисление
- Интегральное исчисление функций одной переменной
- Дифференциальное исчисление функций нескольких переменных
- Отношение в математике
- Математическая логика
- Графы в математике
- Линейные пространства
- Первообразная и неопределенный интеграл
- Линейная функция
- Выпуклые множества точек
- Система координат
