Оглавление:
Возведение в степень — это арифметическая операция, первоначально определяемая как результат многократного умножения числа на себя.
Арифметическим квадратным корнем из неотрицательного числа a называется такое неотрицательное число, квадрат которого равен a.
Что такое степень и корень, как сложить, перемножить, поделить степени, как возвести степень в степень и извлечь корень из степени. Как сложить, перемножить, поделить корни, как возвести в степень и извлечь корень из корня. И как вычислить корень из целого числа, когда он извлекается.
Степени с натуральными показателями
Пусть а — произвольное действительное число, а n — число. Произведение
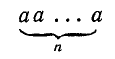
n сомножителей, равных а, называется n-й степенью числа а и обозначается через 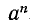 . При этом а называется основанием, а n — показателем степени. При n = 1 просто полагают
. При этом а называется основанием, а n — показателем степени. При n = 1 просто полагают 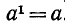 . Таким образом, степень
. Таким образом, степень 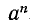 определяется при любых натуральных значениях n. Поскольку действие возведения в натуральную степень определено через действие умножения, то оно рассматривается как рациональное (арифметическое) действие. Отметим некоторые свойства этого действия.
определяется при любых натуральных значениях n. Поскольку действие возведения в натуральную степень определено через действие умножения, то оно рассматривается как рациональное (арифметическое) действие. Отметим некоторые свойства этого действия.
1) При любых натуральных n, m

Это следует из записи
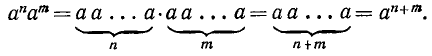
Таким образом, при умножении степеней с одинаковыми основаниями показатели степени складываются.
2) Если 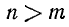 и
и 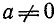 , то
, то

Действительно, это следует из равенства
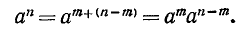
3) При любых натуральных m, n
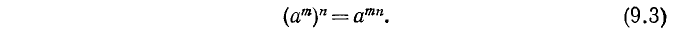
Действительно, по определению n-й степени числа имеем
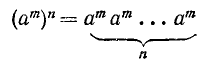
и по свойству 1)
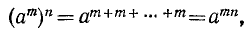
что и требовалось получить.
Итак, при возведении степени в степень показатели степени перемножаются.
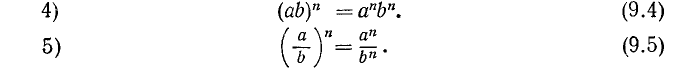
Доказательство свойств 4) и 5) предоставляется читателю.
Степени с целыми показателями
Свойство 2) п. 9:
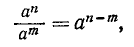
установлено при n > m. При n = m или n < m его правая часть не определена, но левая часть сохраняет смысл. Это дает повод ввести определение степени с нулевым и целыми отрицательными показателями степени.
Нулевую степень числа 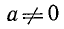 полагают по определению равной единице:
полагают по определению равной единице:
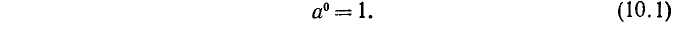
Таким образом, равенство (9.2) становится теперь верным и при n = m .
Степень числа 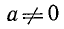 с отрицательным показателем —k определяется равенством
с отрицательным показателем —k определяется равенством
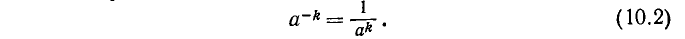
Нулевая и отрицательная степени числа 0 не определяются.
Определение (10.2) делает равенство (9.2) верным и при n < m. Так, если m = n + k, то имеем
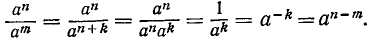
Нетрудно проверить, что все правила действия возведения в натуральную степень, указанные в п. 9, сохраняют силу при введенных определениях и при любых целых показателях степени.
Так, например, проверяем, что
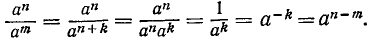
т. е. и для отрицательных показателен степени сохраняет силу правило 1) умножения степеней с одинаковыми основаниями.
Пример:
Вычислить: 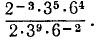
Решение:
Используем то, что 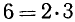 , и применяем правила действий с целыми степенями:
, и применяем правила действий с целыми степенями:
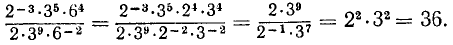
Корни
Если n > 1—натуральное число, а а и b — действительные числа, причем
Ь» = а,
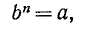
то число b называется корнем n-й степени из числа а. Таким образом, корнем n-й степени из числа а называется каждое число b такое, что его n-я степень равна а.
Действие отыскания корня из числа а называется действием извлечения корня n-й степени из а. Действие извлечения корня степени n является действием, обратным по отношению к действию возведения числа в степень n .
Если n — нечетное число, то, как можно доказать, для любого действительного числа а существует единственное значение корня степени n (в действительной области; извлечение корней в области комплексных чисел рассматривается в п. 18).
Если n — четное, то действие извлечения корня степени n из отрицательного числа невозможно, так как четная степень любого числа неотрицательна. Можно показать, что для любого положительного числа а корень четной степени n имеет два значения, равных по абсолютной величине и противоположных по знаку. Например, числа +3, —3 суть корни квадратные из числа 9. Положительный корень четной степени нз положительного числа называется арифметическим корнем (или арифметическим значением корня). Его единственность видна из такого соображения. Если бы имеюсь два положительных корня 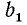 и
и 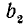 , то одно из чисел
, то одно из чисел 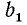 ,
, 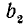 было бы больше другого, например,
было бы больше другого, например, 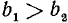 . Но тогда и
. Но тогда и 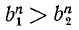 , т. е. оба числа не могли бы быть корнями степени n из одного и того же числа а. Это рассуждение применимо и к случаю корней нечетной степени.
, т. е. оба числа не могли бы быть корнями степени n из одного и того же числа а. Это рассуждение применимо и к случаю корней нечетной степени.
Наметим обоснование утверждения о существовании корня 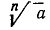 произвольной степени из любого положительного действительного числа. Прежде всего, может случиться, что корень существует в области натуральных чисел. Если это так, то этим задача решается; если в области натуральных чисел корня не имеется, то найдутся два последовательных целых числа k и k +l такие, что
произвольной степени из любого положительного действительного числа. Прежде всего, может случиться, что корень существует в области натуральных чисел. Если это так, то этим задача решается; если в области натуральных чисел корня не имеется, то найдутся два последовательных целых числа k и k +l такие, что 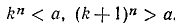 . Теперь будем рассматривать десятичные дроби вида
. Теперь будем рассматривать десятичные дроби вида 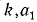 , где
, где 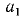 = 0, 1, …, 9. Либо среди них имеется искомый корень, либо снова получим для некоторого
= 0, 1, …, 9. Либо среди них имеется искомый корень, либо снова получим для некоторого 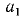
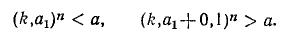
Далее будем искать приближение корня в виде дроби с двумя знаками после запятой и т. д. Таким путем в принципе можно построить ряд десятичных приближений по недостатку и по избытку для некоторого действительного числа, которое и следует принять за значение искомого корня (аналогично примеру 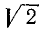 в п. 6).
в п. 6).
Корень степени n обозначается с помощью знака радикала 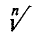 ; при этом для придания символу
; при этом для придания символу 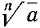 вполне определенного смысла условимся понимать под
вполне определенного смысла условимся понимать под 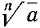 :
:
1) единственное значение корня в случае нечетного n (а в этом случае — любое действительное число).
2) арифметический корень степени n из а в случае четного а (в этом случае а > 0).
Корень из нуля при любом показателе n равен нулю.
В случае, если мы хотим рассматривать оба значения корня четной степенн из положительного числа, то пишем 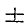
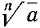 ; если перед корнем четной степени знак не написан, то всегда имеют в виду арифметическое значение корня.
; если перед корнем четной степени знак не написан, то всегда имеют в виду арифметическое значение корня.
В случае корня степени 2 (квадратного корня) пишут просто 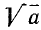 ; например,
; например, 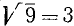 . Корень третьей степени называют кубическим корнем.
. Корень третьей степени называют кубическим корнем.
Если а — произвольное действительное число, то
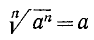
при нечетном n и
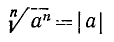
при четном n (в частности, в случае квадратного корня). Так, например, 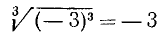 , но
, но 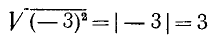 .
.
Укажем основные правила действий над корнями; для простоты предположим, что числа под знаком корня—положительные.
1) Извлечение корня из произведения. Корень из произведения равен произведению корней из сомножителей:
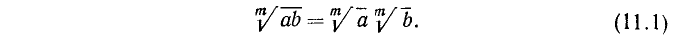
Доказательство:
Для доказательства этого (и дальнейших) свойства достаточно проверить, что при возведении обеих частей равенства (11.1) в степень m получим одно и то же число. При этом мы пользуемся соотношением 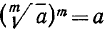 , непосредственно вытекающим из определения корня n-й степени. Имеем
, непосредственно вытекающим из определения корня n-й степени. Имеем
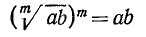
и
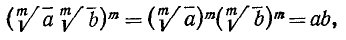
откуда и вытекает требуемое свойство.
2) Возведение корня в степень. Для возведения корня в степень достаточно возвести в, эту степень подкоренное выражение, сохраняя показатель корня.
Это правило записывается так:
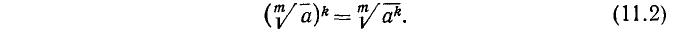
Свойство 2) непосредственно вытекает из свойства 1), а также может быть проверено возведением обеих частей равенства (11.2) в степень m.
3) Извлечение корня из частного. Корень из частного равен частному от деления корня из числителя на корень из знаменателя:
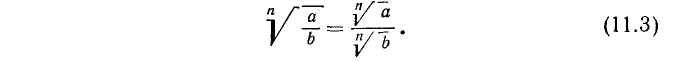
4) Извлечение корня из степени. Пусть показатель степени m является кратным показателя корня n: m = nk. Тогда
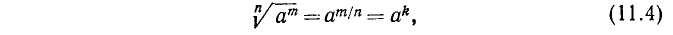
т. е. при извлечении корня из степени показатель степени следует разделить на показатель корня.
Пусть в общем случае m не является кратным n; выполним деление m на n с остатком: m = nq + r. Тогда
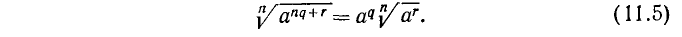
Действительно, применяя уже найденные правила, получим
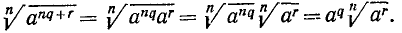
Пример:
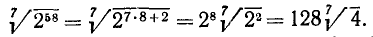
5) Извлечение корня из корня. Для извлечения корня из корня достаточно перемножить показатели корней, сохранив подкоренное выражение:
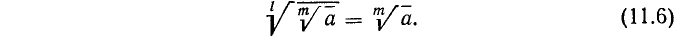
6) Сокращение показателя корня и показателя подкоренного выражения на их общий множитель. Пусть в выражении 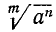 н. о. д. показателей m и n равен k (п. 3). Это значит, что m = kr и n = ks, причем r и s — целые взаимно простые числа. Тогда
н. о. д. показателей m и n равен k (п. 3). Это значит, что m = kr и n = ks, причем r и s — целые взаимно простые числа. Тогда 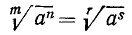 . Это означает, что если показатели корня и подкоренного выражения имеют общий делитель, то на него их можно сократить, не меняя величины корня. Например:
. Это означает, что если показатели корня и подкоренного выражения имеют общий делитель, то на него их можно сократить, не меняя величины корня. Например:
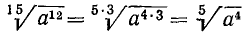
Обратно, если показатели корня и подкоренного выражения умножить на одно и то же число, то корень от этого не изменится. Например:
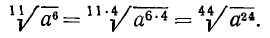
7) Приведение корней к общему показателю. Пользуясь только что установленным свойством, можно два или несколько корней приводить к общему показателю, который представляет собой н. о. к. показателей всех данных корней.
Это преобразование полезно применять при умножении корней с разными показателями.
Пример:
Упростить произведение 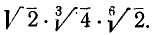
Решение:
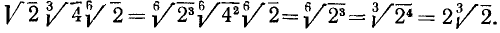
Здесь н. о. к. показателей корней равнялось 6; в процессе преобразования мы применили также правило 6) сокращения показателей степени и корня и правило 1).
Аналогичным образом выполняется и деление корней.
Пример:
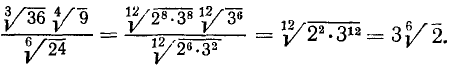
Степени с рациональными показателями
Степени с действительными показателями. Будем, как и в п. 11, рассматривать только корни из положительных чисел. Мы видели, что в случае, когда m делится нацело на n,
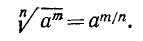
Обобщая это правило, можно ввести следующее определение степени с положительным рациональным показателем p/q:
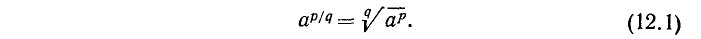
В случае отрицательного рационального показателя степени —p/q полагают (по аналогии со случаем целого отрицательного показателя степени)
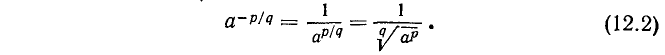
На степени с рациональными показателями распространяются все правила действий над степенями с натуральными и вообще целыми показателями. Для их обоснования достаточно применить правила п. 11 действий над корнями. Докажем, например, свойство
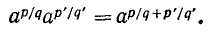
Имеем
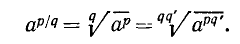
Так же получим 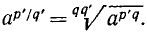 Отсюда
Отсюда
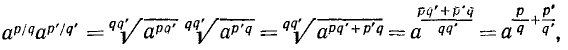
что и требовалось доказать.
Рассматривают также степени положительного числа а при произвольных действительных показателях. В основу определения 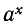 при иррациональном х кладется последовательное приближение х рациональными числами. Так, например, для
при иррациональном х кладется последовательное приближение х рациональными числами. Так, например, для 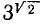 следует рассмотреть приближения по недостатку и по избытку для
следует рассмотреть приближения по недостатку и по избытку для 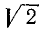 и возводить 3 в соответствующие рациональные степени, записывая
и возводить 3 в соответствующие рациональные степени, записывая
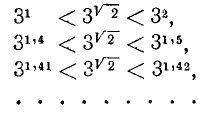
По мере продолжения этого процесса левая и правая части неравенств, выраженные бесконечными десятичными дробями, будут иметь все большее и большее число совпадающих десятичных знаков, которые и будут приниматься за десятичные знаки, определяющие иррациональное число 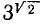 . Более подробно рассматривать этот вопрос мы не можем, но отметим, что
. Более подробно рассматривать этот вопрос мы не можем, но отметим, что 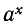 имеет действительное вполне определенное значение при а > 0 и любом действительном х.
имеет действительное вполне определенное значение при а > 0 и любом действительном х.
Замечание:
Извлечение корня нечетной степени возможно и из отрицательного числа. Поэтому выражению 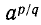 при а < 0 также можно приписать смысл с помощью равенства
при а < 0 также можно приписать смысл с помощью равенства 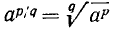 в случае, когда несократимая рациональная дробь p/q имеет нечетный знаменатель. В случае четного q и для иррациональных значений показателя степень отрицательного основания не определяется. Нуль в любой положительной степени равен нулю; нулевая и отрицательные степени нуля не определены.
в случае, когда несократимая рациональная дробь p/q имеет нечетный знаменатель. В случае четного q и для иррациональных значений показателя степень отрицательного основания не определяется. Нуль в любой положительной степени равен нулю; нулевая и отрицательные степени нуля не определены.
Пример:
Произвести действия, пользуясь отрицательными и дробными показателями степени: 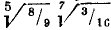 .
.
Решение:
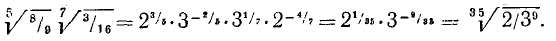
Алгоритм извлечения квадратного корня
Пусть дано произвольное положительное число А; тогда можно указать последовательность арифметических действий, приводящую к вычислению квадратного корня из данного числа с любой заданной степенью точности. Эта последовательность действий, описанная ниже, получает название алгоритма извлечения квадратного корня.
Предположим вначале для простоты, что данное число — целое m-значное; записываем его в виде 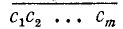 (см. п. 1). Ответим на вопрос, сколько цифр будет содержать целая часть арифметического квадратного корня из А. Ответ получается из следующего сравнения неравенств для числа и корня из этого числа:
(см. п. 1). Ответим на вопрос, сколько цифр будет содержать целая часть арифметического квадратного корня из А. Ответ получается из следующего сравнения неравенств для числа и корня из этого числа:

Таким образом, если А — одно- или двузначное число, то целая часть 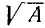 — однозначная; если А — трех- или четырехзначное число, то целая часть
— однозначная; если А — трех- или четырехзначное число, то целая часть 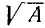 — двузначная и т. д. Вообще, если А — m-значное число, то целая часть
— двузначная и т. д. Вообще, если А — m-значное число, то целая часть 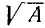 будет (m/2)-значной при четном m и ((m + 1)/2) — значной при нечетном m. Практически это число знаков определяется механически таким образом: число А разбивают на «грани» по две цифры, начиная справа; при этом последняя левая грань может состоять из одной или двух цифр, например:
будет (m/2)-значной при четном m и ((m + 1)/2) — значной при нечетном m. Практически это число знаков определяется механически таким образом: число А разбивают на «грани» по две цифры, начиная справа; при этом последняя левая грань может состоять из одной или двух цифр, например:
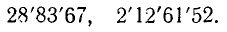
Число граней и дает нам число цифр целой части 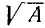 .
.
Следующий шаг состоит в определении первой цифры числа 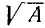 ; эта цифра
; эта цифра 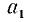 легко находится в уме, так как для ее отыскания достаточно помнить квадраты целых чисел от 1 до 9. В самом деле, первая цифра
легко находится в уме, так как для ее отыскания достаточно помнить квадраты целых чисел от 1 до 9. В самом деле, первая цифра 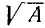 зависит только от первой (считая слева) грани числа А. Например, содержит
зависит только от первой (считая слева) грани числа А. Например, содержит 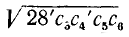 заведомо 5 сотен независимо от цифр
заведомо 5 сотен независимо от цифр 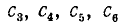 ;
; 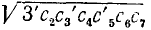 содержит одну тысячу независимо от цифр
содержит одну тысячу независимо от цифр 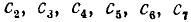 и т. п. Можно записать
и т. п. Можно записать
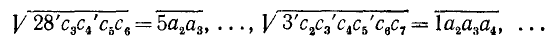
Покажем, из каких соображений можно находить следующую цифру 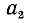 числа
числа 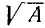 . Цифра
. Цифра 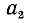 определяется как наибольшая цифра, при которой еще выполняется неравенство (k — число граней А)
определяется как наибольшая цифра, при которой еще выполняется неравенство (k — число граней А)
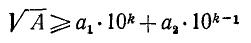
или
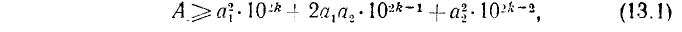
откуда, тем более,
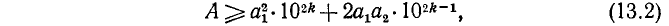
или
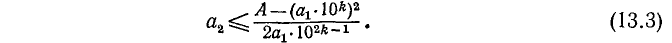
Можно было бы находить 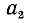 из неравенства (13.1), но решение квадратного неравенства является трудоемким; поэтому переходят к простому линейному неравенству (13.2), из которого и получается условие (13.3) для подбора
из неравенства (13.1), но решение квадратного неравенства является трудоемким; поэтому переходят к простому линейному неравенству (13.2), из которого и получается условие (13.3) для подбора 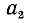 . Берем наибольшее целое
. Берем наибольшее целое 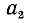 , удовлетворяющее условию (13.3).
, удовлетворяющее условию (13.3).
Такое 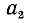 может еще оказаться слишком большим: надо проверить, выполняется ли и неравенство (13.1); если
может еще оказаться слишком большим: надо проверить, выполняется ли и неравенство (13.1); если 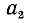 оказалось слишком большим, то уменьшаем его на единицу и снова проверяем, удовлетворяется ли неравенство (13.1). Таким образом подбирается
оказалось слишком большим, то уменьшаем его на единицу и снова проверяем, удовлетворяется ли неравенство (13.1). Таким образом подбирается 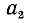 .
.
При этом 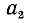 определяется с использованием лишь первых двух левых граней A, остальные грани А на выбор
определяется с использованием лишь первых двух левых граней A, остальные грани А на выбор 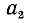 не влияют.
не влияют.
Пример:
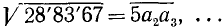 ; для отыскания
; для отыскания 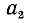 имеем неравенство (13.3), которое запишется так:
имеем неравенство (13.3), которое запишется так:
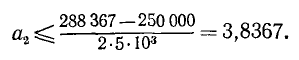
Наибольшее значение 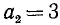 . Проверяем, удовлетворяется ли неравенство (13.1):
. Проверяем, удовлетворяется ли неравенство (13.1):
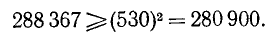
Так как неравенство выполнено, то вторая цифра корня равна 3:
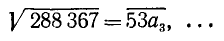
Пример:
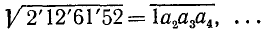 , для
, для 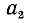 имеем
имеем
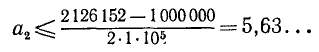
Наибольшее возможное значение 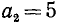
но неравенство
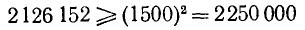
неверно. Испытываем 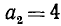 :
:
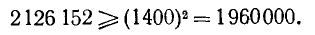
Неравенство выполнено. Итак,
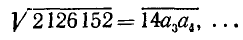
Замечание:
Здесь практически можно было определить первые две цифры корня сразу, в уме, так как очевидно, что 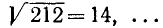
После того как найдены первые две цифры корня 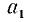 и
и 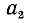 , из тех же соображений находят следующие, в том числе и идущие после запятой цифры
, из тех же соображений находят следующие, в том числе и идущие после запятой цифры 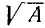 . Например, для
. Например, для 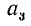 исходят из неравенства
исходят из неравенства
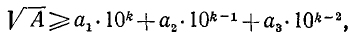
получая из него оценку для 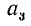 :
:
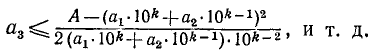
При практическом извлечении корня все вычисления располагают в некоторой определенной схеме, которую мы напомним на тех же примерах 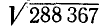 и
и 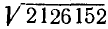 .
.
Перед разбором примеров приведем для удобства формулировку правила извлечения корня.
Правило. Чтобы извлечь квадратный корень из данного целого числа, разбивают его справа налево на грани, по две цифры в каждой, кроме первой (крайней левой), в которой может быть и одна цифра.
Чтобы найти первую цифру корня, извлекают квадратный корень из первой грани.
Чтобы найти вторую цифру, из первой грани вычитают квадрат первой цифры корня, к остатку сносят вторую грань и число десятков получающегося числа делят на удвоенную первую цифру корня; полученное целое число подвергают испытанию.
Испытание это производится так: за вертикальной чертой корня (налево от остатка) пишут удвоенное ранее найденное число корня и к нему с правой стороны приписывают испытуемую цифру; получившееся после этой приписки число умножают на испытуемую цифру. Если после умножения получится число, большее остатка, то испытуемая цифра не годится и надо испытывать следующую, меньшую цифру.
Следующие цифры корня находят с помощью того же приема.
Если после снесения грани число десятков получившегося числа окажется меньше делителя, т. е. меньше удвоенной найденной части корня, то в корне ставят 0, сносят следующую грань и продолжают действие дальше.
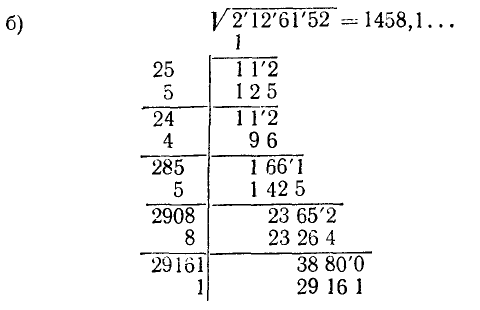
Пример:
Вычислить: а) 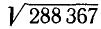 с точностью до 0,01; б)
с точностью до 0,01; б) 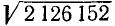 с точностью до 0,1.
с точностью до 0,1.
Решение:

Примечания:
*) Цифра 7 не выдерживает испытания; переходим к следующей цифре 6. **) Мысленно дополняем подкоренное число нулями за запятой и сносим следующую нулевую грань.
Если подкоренное число выражается десятичной дробью, то деление на грани производится от запятой: для целой части влево, для дробной — вправо:
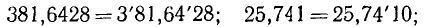
в остальном процесс извлечения корня остается тем же.
Степени с целым показателем
Мы определили выше степень с натуральным показателем. Ясно, что это определение не годится ни для целых отрицательных, ни для дробных показателей — нельзя взять число сомножителем ни —5, ни 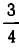 раза. В то же время для многих задач физики нужно определить не только степень с рациональным показателем, но даже и степень с иррациональным показателем.
раза. В то же время для многих задач физики нужно определить не только степень с рациональным показателем, но даже и степень с иррациональным показателем.
В физике часто встречаются величины, обладающие следующим свойством: за равные промежутки времени величина изменяется в одно и то же число раз. Например, если за первый час своего изменения величина уменьшилась втрое, то и за десятый час она тоже уменьшится втрое. Примером такой величины является масса радиоактивного вещества. Пусть в начале наблюдения был 1 кг этого вещества, а после первых суток осталось а кг, то есть количество вещества изменилось в а раз. Тогда, как показывают опыты, в течение вторых суток количество вещества тоже изменится в а раз. Поэтому после вторых суток останется 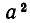 кг вещества. Точно так же в течение третьих суток количество вещества изменится в а раз, и потому останется
кг вещества. Точно так же в течение третьих суток количество вещества изменится в а раз, и потому останется 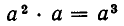 кг вещества.
кг вещества.
Таким же образом изменяются все остальные величины, обладающие указанным выше свойством. Именно если в начале наблюдения значение этой величины равняется М, а через 1 единицу времени это значение изменилось в а раз и стало равно Ма, то через n единиц времени значение величины равно

Поскольку величина промежутка времени стоит в показателе формулы (1), закон изменения (1) называют показательным.
Формула (1) не дает ответа на вопросы, чему равно значение величины через 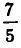 единицы времени, или за 3 единицы времени до начала наблюдения и т. д.
единицы времени, или за 3 единицы времени до начала наблюдения и т. д.
Естественно обозначить значение величины через t единиц времени после начала наблюдения так: 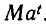 При этом t может быть как целым, так и дробным, как положительным, так и oтрицательным (в последнем случае речь идет о моментах времени, предшествовавших началу наблюдения). Но чтобы формула
При этом t может быть как целым, так и дробным, как положительным, так и oтрицательным (в последнем случае речь идет о моментах времени, предшествовавших началу наблюдения). Но чтобы формула 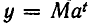 получила смысл, надо обобщить понятие о степени, ввести степени не только с натуральными, но и с произвольными показателями. Мы решим задачу о распространении понятия степени на случай целых показателей — положительных, отрицательных и равных нулю.
получила смысл, надо обобщить понятие о степени, ввести степени не только с натуральными, но и с произвольными показателями. Мы решим задачу о распространении понятия степени на случай целых показателей — положительных, отрицательных и равных нулю.
При обобщении понятия степени мы будем руководствоваться следующим требованием.
Для степеней с любыми показателями должны оставаться в силе основные свойства степеней с натуральными показателями:
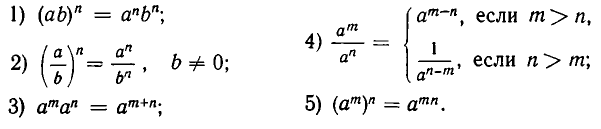
Иными словами, эти свойства должны оставаться справедливыми не только для натуральных, но и для любых показателей. Обычно мы будем пользоваться одним из этих свойств для введения соответствующего определения, после чего будем проверять выполнение остальных свойств.
Отметим, что два подхода — с точки зрения физики и с точки зрения математики — согласуются друг с другом.
Выясним физический смысл свойств 3) и 5). Пусть сначала прошло m единиц времени, а потом n единиц времени. За первые m единиц времени величина изменится в 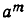 раз, а за следующие n единиц времени она изменится в
раз, а за следующие n единиц времени она изменится в 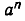 раз. Поэтому за m+n единиц времени она изменится в
раз. Поэтому за m+n единиц времени она изменится в 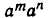 раз. Но, с другой стороны, за m+n единиц времени она изменяется в
раз. Но, с другой стороны, за m+n единиц времени она изменяется в 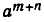 . Значит, должно выполняться равенство
. Значит, должно выполняться равенство 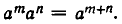 При этом т и п могут быть произвольными, а не только натуральными числами.
При этом т и п могут быть произвольными, а не только натуральными числами.
Аналогично истолковывается смысл свойства 5). Примем m единиц времени за новую единицу измерения (например, перейдем от секунд к минутам или часам). Тогда за одну новую единицу измерения времени наша величина изменяется в 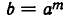 раз, а за n новых единиц времени — в
раз, а за n новых единиц времени — в 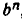 , то есть в
, то есть в 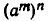 раз. Но n новых единиц времени равно mn первоначальных единиц, а по условию за mn единиц времени величина меняется в
раз. Но n новых единиц времени равно mn первоначальных единиц, а по условию за mn единиц времени величина меняется в 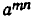 раз. Значит,
раз. Значит, 
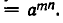 И здесь m и n могут быть любыми, а не только натуральными числами.
И здесь m и n могут быть любыми, а не только натуральными числами.
Степень с нулевым показателем
Рассмотрим равенство

Пока что оно имеет смысл лишь при натуральных значениях n. Выясним, как надо определить 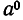 , чтобы равенство (1) выполнялось и при n = 0. Положим в (1) n = 0. Тогда равенство примет вид
, чтобы равенство (1) выполнялось и при n = 0. Положим в (1) n = 0. Тогда равенство примет вид
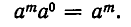
Отсюда ясно, что при 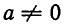 надо положить
надо положить 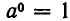 . Значение 0° не определяется.
. Значение 0° не определяется.
Проверим, согласуется ли это определение с физическим подходом. Мы рассматриваем величины, которые в момент времени t принимают значение 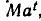 где М — значение величины при t = 0. Поэтому должно вы полнятся равенство
где М — значение величины при t = 0. Поэтому должно вы полнятся равенство 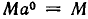 , из которого и следует, что
, из которого и следует, что 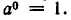
Степень с целым отрицательным показателем
Определим степень с целым отрицательным показателем — n (то есть 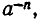 где n — натуральное) так, чтобы равенство
где n — натуральное) так, чтобы равенство 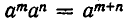 выполнялось не только для натуральных и нулевых значений m и n, но для всех целых значений. Положим в этом равенстве m = —n. Мы получим тогда, что
выполнялось не только для натуральных и нулевых значений m и n, но для всех целых значений. Положим в этом равенстве m = —n. Мы получим тогда, что
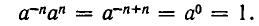
Отсюда следует, что при 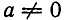 надо положить
надо положить
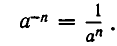
При а =0 выражение 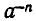 не определяется.
не определяется.
Снова проверим, насколько согласуется введенное определение с физическим смыслом, который был придан значению 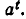 Теперь нам надо найти значение величины при t = —n, то есть за n единиц времени до начала измерения. Обозначим это значение через m. Так как в течение каждой единицы времени значение величины изменяется в а раз, то за n единиц времени значение величины изменится в
Теперь нам надо найти значение величины при t = —n, то есть за n единиц времени до начала измерения. Обозначим это значение через m. Так как в течение каждой единицы времени значение величины изменяется в а раз, то за n единиц времени значение величины изменится в 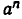 раз и станет равным
раз и станет равным 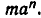 Но по условию при t = 0 значение величины равно М . Поэтому
Но по условию при t = 0 значение величины равно М . Поэтому 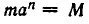 , значит,
, значит, 
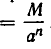 . С другой стороны, при t = —n значение величины должно равняться
. С другой стороны, при t = —n значение величины должно равняться 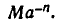 Поэтому
Поэтому 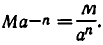 Мы снова пришли к тому же результату:
Мы снова пришли к тому же результату: 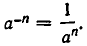
Мы распространили понятие степени на случай любого целого показателя — положительного, отрицательного и нулевого. Покажем, что при этом выполняются свойства 1) — 5) степеней, сформулированные в п. 1 (при этом, конечно, основания степеней должны отличаться от нуля).
Докажем, что выполняется равенство 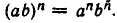 Если n = 0, то оно принимает вид
Если n = 0, то оно принимает вид 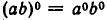 и, очевидно, имеет место, так как
и, очевидно, имеет место, так как 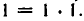 Пусть теперь n = — k — целое отрицательное число. Тогда k > 0 и потому
Пусть теперь n = — k — целое отрицательное число. Тогда k > 0 и потому
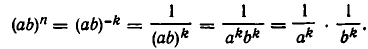
Но 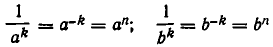 и потому имеем
и потому имеем
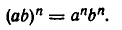
Тем самым доказано выполнение равенства 1) и при целых отрицательных значениях n.
Точно так же доказывается выполнение равенства 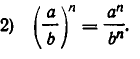
Доказательство выполнения свойства 3) 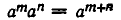 несколько сложнее, так как приходится разбирать несколько случаев, в зависимости от знаков чисел m , n и m+n. Мы разберем один из этих случаев, когда m>0, n<0, m+n>0. Обозначим n через — k. Тогда m — k >0 и потому
несколько сложнее, так как приходится разбирать несколько случаев, в зависимости от знаков чисел m , n и m+n. Мы разберем один из этих случаев, когда m>0, n<0, m+n>0. Обозначим n через — k. Тогда m — k >0 и потому
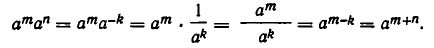
Предоставляем читателю разобрать остальные случаи (включая и те, когда одно из чисел m, n, m+n обращается в нуль). Доказательство равенства 4)
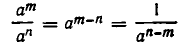
проводится тем же способом.
Наконец, докажем соотношение 5): 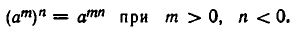 Положим n = —k. Тогда mn = — mk и потому
Положим n = —k. Тогда mn = — mk и потому
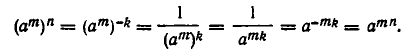
Случаи, когда m и n имеют иные знаки или обращаются в нуль, разбираются точно так же. Например, 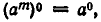 поскольку обе части равенства равны 1
поскольку обе части равенства равны 1
Итак, для степеней с любым целым показателем выполняются свойства 1) — 5) из п. 1. Отметим еще некоторые свойства этих степеней.
Если а — положительное число, то для всех целых значений n число 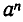 положительно.
положительно.
Имеют место равенства:

и
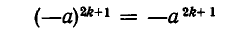
(здесь k обозначает любое целое число). Отсюда следует, что если а — отрицательное число, то 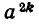 положительно, а
положительно, а 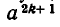 отрицательно.
отрицательно.
Примеры:
Вычислить выражение
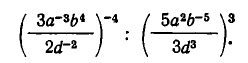
Сначала выполним указанные действия, а потом освободимся от отрицательных показателей. Итак, наше выражение равно:
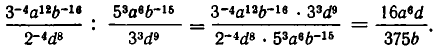
Корни. Степени с рациональными показателями
Пусть а — положительное число и n — натуральное число. Можно доказать, что существует одно и только одно положительное число b такое, что 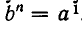 Это число называют арифметическим корнем n-й степени из а и обозначают
Это число называют арифметическим корнем n-й степени из а и обозначают 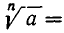
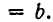 Итак, если а и b — положительные числа, то записи
Итак, если а и b — положительные числа, то записи

и

обозначают одно и то же.
Число а называют подкоренным выражением, а n—показателем корня. Принято при n = 2 опускать показатель корня. Поэтому 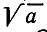 означает
означает 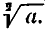
Отметим, что наряду со словом «корень» употребляют слово «радикал». Мы будем применять этот термин в тех случаях, когда корень из числа можно спутать с корнем уравнения.
Введем понятие алгебраического корня. Говорят, что число b является алгебраическим корнем n-й степени из числа а, если 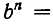
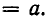 Таким образом, по сравнению с понятием арифметического корня здесь опускается требование положительности чисел а и b. Если n =2k — четное число и а > 0, то существуют два алгебраических корня степени 2k из а, а именно
Таким образом, по сравнению с понятием арифметического корня здесь опускается требование положительности чисел а и b. Если n =2k — четное число и а > 0, то существуют два алгебраических корня степени 2k из а, а именно 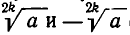 (обозначение
(обозначение 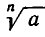 мы сохраняем здесь для арифметического корня). В самом деле,
мы сохраняем здесь для арифметического корня). В самом деле,
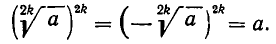
Так как четная степень любого действительного числа неотрицательна, то из отрицательного числа нельзя извлечь действительного корня четной степени. Позже мы познакомимся с комплексными числами, введение которых позволяет определять корни четной степени и из отрицательных чисел.
Если n=2k+1 — нечетное число, то из любого действительного числа а можно извлечь корень степени n. Именно если а >0, то этим корнем является 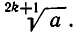 Если же а<0 , то этот корень имеет вид—
Если же а<0 , то этот корень имеет вид— 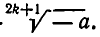 В самом деле, — а >0 и потому
В самом деле, — а >0 и потому
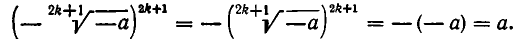
Степени с рациональными показателями
Были определены степени с любыми целыми показателями. Обобщим далее понятие степени, введя степени с любыми рациональными показателями. Это обобщение тесно связано с понятием корня.
Пусть r — рациональное число и а — положительное число. Запишем число r в виде дроби  , где p и q — целые числа. Не теряя общности, можно считать, что q>0 (например,
, где p и q — целые числа. Не теряя общности, можно считать, что q>0 (например, 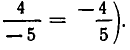
Нам надо определить выражение 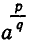 так, чтобы сохранились все свойства степеней. В частности, должно выполняться равенство:
так, чтобы сохранились все свойства степеней. В частности, должно выполняться равенство:

Из него следует, что 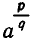 надо определить как корень q-й степени из
надо определить как корень q-й степени из 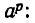

Мы ограничиваемся при этом арифметическими значениями корней
При р = 1 получаем:

Например,
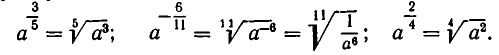
При  мы не определяем смысл выражения
мы не определяем смысл выражения 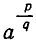 ,
, 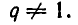 Ясно, что при определении (3) для выражения
Ясно, что при определении (3) для выражения 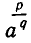 выполняется соотношение (1).
выполняется соотношение (1).
В следующем пункте мы выведем свойства степеней с рациональными показателями. Нам понадобятся для этого следующие два утверждения. а) Если а и b — положительные числа, причем а>b, и если n — натуральное число, то 
Докажем это утверждение индукцией по n. При n = 1 оно имеет место. Пусть уже доказано, что 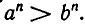 Умножая соответствующие части неравенств
Умножая соответствующие части неравенств 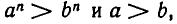 получаем, что
получаем, что  В силу принципа математической индукции неравенство
В силу принципа математической индукции неравенство  верно для всех натуральных значений n.
верно для всех натуральных значений n.
Другое доказательство этого неравенства следует из тождества
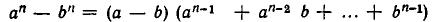
Если а > b, а > 0 и b>0, то обе скобки в правой части равенства положительны и потому
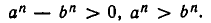
Из свойства а) непосредственно вытекает следующее утверждение:
б) Если а и b — такие положительные числа, что для некоторого натурального числа n имеем 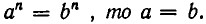
В самом деле, если бы мы имели, например, а >b, то по свойству а) выполнялось бы неравенство  вопреки предположению.
вопреки предположению.
Каждое рациональное число можно различными способами записать в виде дроби. Например, 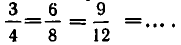 Определение степени с рациональным показателем на первый взгляд зависит от способа записи показателя в виде дроби. Покажем, что это не так, то есть что для любого натурального числа n при а > 0 выполняется равенство:
Определение степени с рациональным показателем на первый взгляд зависит от способа записи показателя в виде дроби. Покажем, что это не так, то есть что для любого натурального числа n при а > 0 выполняется равенство:

Для этого возведем обе части равенства (4) в степень qn. В силу свойства 5) степеней с натуральным показателем и равенства (1) имеем:
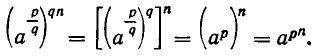
С другой стороны, по формуле (1),
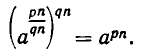
Таким образом, qn-е степени обеих частей доказываемого равенства (4) совпадают. В силу утверждения б) отсюда вытекает справедливость равенства (4).
Можно доказать, что определение (2) согласуется с физическим смыслом степеней с показателем 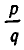 (см. стр. 93).
(см. стр. 93).
Свойства степеней с рациональными показателями
Докажем, что для степеней с рациональными показателями сохраняются основные свойства степеней с натуральными показателями.
Сначала докажем, что при х >О, у >0 и любом рациональном r

Пусть 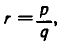 , где q > 0. Тогда равенство (1) примет вид
, где q > 0. Тогда равенство (1) примет вид

Возведем обе части равенства (1′) в степень q. В силу формулы (I), п. 2, и свойства 1) степеней с натуральным показателем имеем:
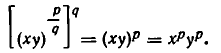
С другой стороны
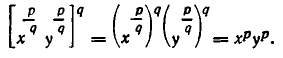
Мы доказали, что q-е степени обеих частей доказываемого равенства (1) имеют одно и то же значение 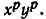 Поэтому по утверждению б), п. 2, справедливо и равенство
Поэтому по утверждению б), п. 2, справедливо и равенство 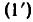 . Но тогда справедливо и равенство (1).
. Но тогда справедливо и равенство (1).
Совершенно так же доказывается, что если х > 0 и у > 0, а r — рациональное число, то

Теперь докажем, что при х > 0 для любых рациональных чисел г, и г2 выполняется равенство:

Сначала рассмотрим случай, когда 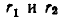 изображаются дробями с одинаковыми знаменателями:
изображаются дробями с одинаковыми знаменателями:
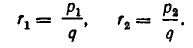
В этом случае доказываемое равенство принимает вид:

Возведем обе части этого равенства в степень q. Мы получим, что
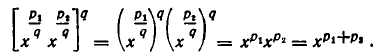
С другой стороны 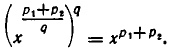
Таким образом, q-е степени обеих частей равенства (4) имеют одно и то же значение 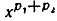 , а потому равенство (4) справедливо.
, а потому равенство (4) справедливо.
Итак, равенство (3) доказано для случая, когда 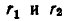 изображаются дробями с одинаковым знаменателем. Но любые два рациональных числа можно представить в виде дробей с одинаковыми знаменателями: если
изображаются дробями с одинаковым знаменателем. Но любые два рациональных числа можно представить в виде дробей с одинаковыми знаменателями: если 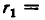
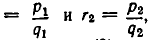 то можно положить
то можно положить 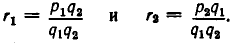 Поэтому равенство (3) верно для любых рациональных чисел
Поэтому равенство (3) верно для любых рациональных чисел 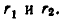
Совершенно так же доказывается выполнение равенства

для положительных х и рациональных 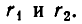
Наконец, докажем, что если х — положительное число и 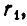
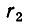 — рациональные числа, то
— рациональные числа, то 
В самом деле, пусть 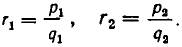 Нам надо доказать, что
Нам надо доказать, что

Для этого возведем обе части равенства (7) в степень 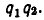 По формуле (1) п. 2, мы имеем
По формуле (1) п. 2, мы имеем
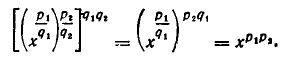
С другой стороны,
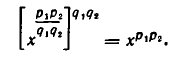
Так как 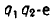 степени обеих частей доказываемого равенства (7) имеют одно и то же значение
степени обеих частей доказываемого равенства (7) имеют одно и то же значение 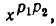 то это равенство справедливо. Тем самым доказано и равенство (6).
то это равенство справедливо. Тем самым доказано и равенство (6).
Решение заданий и задач по предметам:
Дополнительные лекции по высшей математике:
- Тождественные преобразования алгебраических выражений
- Функции и графики
- Преобразования графиков функций
- Квадратная функция и её графики
- Алгебраические неравенства
- Неравенства
- Неравенства с переменными
- Прогрессии в математике
- Арифметическая прогрессия
- Геометрическая прогрессия
- Показатели в математике
- Логарифмы в математике
- Исследование уравнений
- Уравнения высших степеней
- Уравнения высших степеней с одним неизвестным
- Комплексные числа
- Непрерывная дробь (цепная дробь)
- Алгебраические уравнения
- Неопределенные уравнения
- Соединения
- Бином Ньютона
- Число е
- Непрерывные дроби
- Функция
- Исследование функций
- Предел
- Интеграл
- Двойной интеграл
- Тройной интеграл
- Интегрирование
- Неопределённый интеграл
- Определенный интеграл
- Криволинейные интегралы
- Поверхностные интегралы
- Несобственные интегралы
- Кратные интегралы
- Интегралы, зависящие от параметра
- Квадратный трехчлен
- Производная
- Применение производной к исследованию функций
- Приложения производной
- Дифференциал функции
- Дифференцирование в математике
- Формулы и правила дифференцирования
- Дифференциальное исчисление
- Дифференциальные уравнения
- Дифференциальные уравнения первого порядка
- Дифференциальные уравнения высших порядков
- Дифференциальные уравнения в частных производных
- Тригонометрические функции
- Тригонометрические уравнения и неравенства
- Показательная функция
- Показательные уравнения
- Обобщенная степень
- Взаимно обратные функции
- Логарифмическая функция
- Уравнения и неравенства
- Положительные и отрицательные числа
- Алгебраические выражения
- Иррациональные алгебраические выражения
- Преобразование алгебраических выражений
- Преобразование дробных алгебраических выражений
- Разложение многочленов на множители
- Многочлены от одного переменного
- Алгебраические дроби
- Пропорции
- Уравнения
- Системы уравнений
- Системы уравнений высших степеней
- Системы алгебраических уравнений
- Системы линейных уравнений
- Системы дифференциальных уравнений
- Арифметический квадратный корень
- Квадратные и кубические корни
- Извлечение квадратного корня
- Рациональные числа
- Иррациональные числа
- Арифметический корень
- Квадратные уравнения
- Иррациональные уравнения
- Последовательность
- Ряды сходящиеся и расходящиеся
- Тригонометрические функции произвольного угла
- Тригонометрические формулы
- Обратные тригонометрические функции
- Теорема Безу
- Математическая индукция
- Показатель степени
- Показательные функции и логарифмы
- Множество
- Множество действительных чисел
- Числовые множества
- Преобразование рациональных выражений
- Преобразование иррациональных выражений
- Геометрия
- Действительные числа
- Степень с рациональным показателем
- Тригонометрические функции угла
- Тригонометрические функции числового аргумента
- Тригонометрические выражения и их преобразования
- Преобразование тригонометрических выражений
- Комбинаторика
- Вычислительная математика
- Прямая линия на плоскости и ее уравнения
- Прямая и плоскость
- Линии и уравнения
- Прямая линия
- Уравнения прямой и плоскости в пространстве
- Кривые второго порядка
- Кривые и поверхности второго порядка
- Числовые ряды
- Степенные ряды
- Ряды Фурье
- Преобразование Фурье
- Функциональные ряды
- Функции многих переменных
- Метод координат
- Гармонический анализ
- Вещественные числа
- Предел последовательности
- Аналитическая геометрия
- Аналитическая геометрия на плоскости
- Аналитическая геометрия в пространстве
- Функции одной переменной
- Высшая алгебра
- Векторная алгебра
- Векторный анализ
- Векторы
- Скалярное произведение векторов
- Векторное произведение векторов
- Смешанное произведение векторов
- Операции над векторами
- Непрерывность функций
- Предел и непрерывность функций нескольких переменных
- Предел и непрерывность функции одной переменной
- Производные и дифференциалы функции одной переменной
- Частные производные и дифференцируемость функций нескольких переменных
- Дифференциальное исчисление функции одной переменной
- Матрицы
- Линейные и евклидовы пространства
- Линейные отображения
- Дифференциальные теоремы о среднем
- Теория устойчивости дифференциальных уравнений
- Функции комплексного переменного
- Преобразование Лапласа
- Теории поля
- Операционное исчисление
- Системы координат
- Рациональная функция
- Интегральное исчисление
- Интегральное исчисление функций одной переменной
- Дифференциальное исчисление функций нескольких переменных
- Отношение в математике
- Математическая логика
- Графы в математике
- Линейные пространства
- Первообразная и неопределенный интеграл
- Линейная функция
- Выпуклые множества точек
- Система координат
